第十四届蓝桥杯省赛C++B组E题【接龙数列】题解(AC)




需求分析
题目要求最少删掉多少个数后,使得数列变为接龙数列。
相当于题目要求求出数组中的最长接龙子序列。
题目分析
对于一个数能不能放到接龙数列中,只关系到这个数的第一位和最后一位,所以我们可以先对数组进行预处理,将所有的数变为两位数,例如 12345 → 15 12345 \rightarrow 15 12345→15, 6 → 66 6 \rightarrow 66 6→66, … \dots …,这样当我们需要取出一个数 x x x 的第一位时,只需要计算 x / 10 x / 10 x/10,取出最后一位时,只需要计算 x % 10 x \% 10 x%10。
那么接下来考虑如何求接龙序列的最大值。
考虑动态规划, f ( i , j ) f(i, j) f(i,j) 表示在前 i i i 个数中,以 j j j 结尾的最大长度。
考虑状态转移,设第 i i i 个数为 a b ab ab:
- 若不选第 i i i 个数,则有 f ( i , j ) = f ( i − 1 , j ) f(i, j) = f(i - 1, j) f(i,j)=f(i−1,j)( 0 ≤ j ≤ 9 0 \leq j \leq 9 0≤j≤9)。
- 若选第 i i i 个数,则 f ( i , b ) = max ( f ( i − 1 , b ) , f ( i − 1 , a ) + 1 ) f(i, b) = \max(f(i - 1, b), f(i - 1, a) + 1) f(i,b)=max(f(i−1,b),f(i−1,a)+1)
那么接龙数列的最大长度为 max ( { f ( n , i ) \max(\{f(n, i) max({f(n,i)( 0 ≤ i ≤ 9 0 \leq i \leq 9 0≤i≤9) } ) \}) })。
观察状态转移发现, f ( i , j ) f(i, j) f(i,j) 仅由 f ( i − 1 , x ) f(i - 1, x) f(i−1,x) 计算得出,故可以使用滚动数组进行优化。
时间复杂度 O ( n ) O(n) O(n)。
- C++
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1e5 + 10;int n;
int q[N];
int f[N][10];int main()
{cin >> n;for (int i = 1; i <= n; ++ i ){int x;cin >> x;int y = x % 10;while (x >= 10)x /= 10;q[i] = x * 10 + y;}for (int i = 1; i <= n; ++ i ){for (int j = 0; j < 10; ++ j )f[i][j] = f[i - 1][j];int a = q[i] / 10, b = q[i] % 10;f[i][b] = max(f[i][b], f[i - 1][a] + 1);}int res = 0;for (int i = 0; i < 10; ++ i )res = max(res, f[n][i]);cout << n - res << endl;return 0;
}
- C++(空间优化)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1e5 + 10;int n;
int q[N];
int f[N];int main()
{cin >> n;for (int i = 0; i < n; ++ i ){int x;cin >> x;int y = x % 10;while (x >= 10)x /= 10;q[i] = x * 10 + y;}for (int i = 0; i < n; ++ i ){int a = q[i] / 10, b = q[i] % 10;f[b] = max(f[b], f[a] + 1);}cout << n - *max_element(f, f + 10) << endl;return 0;
}
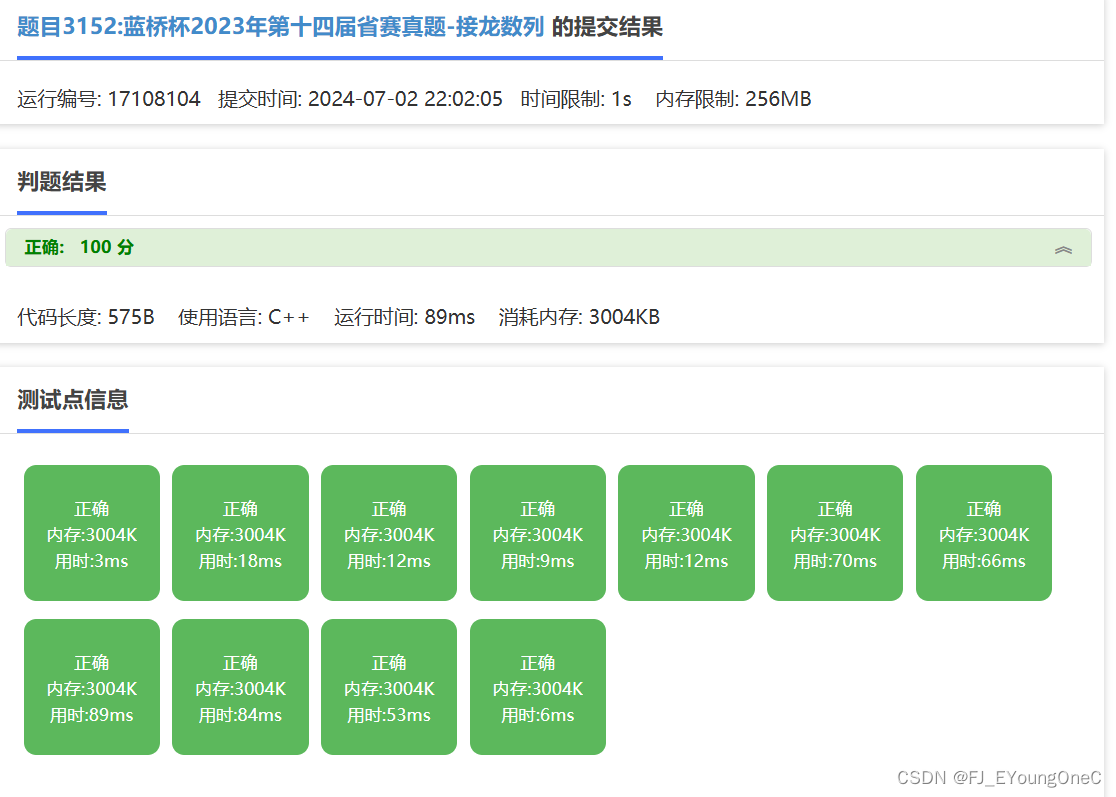
【在线测评】