IO多路复用--[select | poll | epoll | Reactor]
因为在简历上写了netty的项目,因此还是将网络底层的那点东西搞清楚。
首先希望明确的是,BIO、NIO、IO多路复用这是不同的东西, 我会在本文中详细讲出来。
本文参考资料:
JAVA IO模型
IO多路复用 select poll epoll介绍
从BIO到epoll
UNIX网络编程 推荐看一下
1. BIO与NIO
在一次输入操作中,有两个不同的阶段:
- 等待内核态的数据准备完毕。(比如说输入操作是读取磁盘,那么我们需要等待磁盘寻址、加载到内存,这些过程就是数据准备阶段)
- 将内核态的数据拷贝到用户态。(在数据准备完毕后,为了用户态的程序使用,需要将内核态的数据拷贝给用户态,这个阶段用时很小)。
BIO的读取流程

BIO的读取流程很简单,对于每一个进行读取操作的线程,线程从接受这个读取请求到最终将数据返回用户态的整个过程都是阻塞的。举个小例子,如果使用BIO读取磁盘文件,那么读取线程在 {等待磁盘寻址、页加载等数据准备流程,最终将数据从内核态拷贝到用户态} 这整个流程中都是被阻塞的。
NIO的读取流程
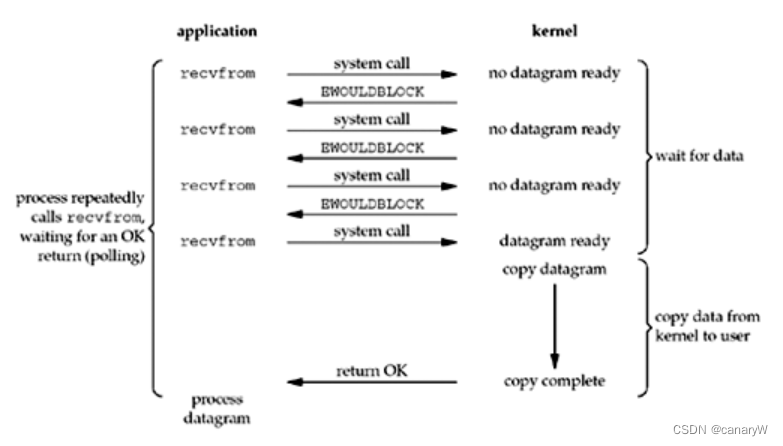
在BIO中,阻塞操作极大地影响了线程的利用率:线程在准备数据阶段无事可做,但是却不能抽身去处理其他的IO操作。因此NIO就是解决这个事情,NIO在接收IO请求时,并不会在数据处理阶段阻塞住,而是不断地询问这个文件描述符:你的数据准备好了吗。如果准备好了的话那么就将数据从内核态拷贝到用户态,然后返回。
可以看出,NIO并不是在全过程都是非阻塞的,而是在数据准备阶段非阻塞,在数据拷贝阶段阻塞。但是由于数据拷贝阶段时间很短,因此几乎相当于非阻塞。
上面这么说有点抽象,我们来聊一聊怎么使用NIO去进行读取。
- 假设说我们现在有100个客户端连接,在linux中一切即文件,因此我们具有100个文件描述符
fd。 - 我们在一个
while循环中不断地遍历这100个fd,去查看其数据是否准备好,一旦准备好了,那么就进行数据拷贝阶段,这个fd的IO过程随之结束。如果没有准备好,我们继续对其遍历。 - 写成代码格式就是这样:
// 具有一系列文件描述符
fds = [fd1, fd2...]while(true){for (fd in fds){// 判断fd中的数据是否准备完毕// 这个过程会涉及系统调用,因为文件描述符是内核态的东西boolean ready = is_ready(fd)if (ready){// 进行数据拷贝等一系列操作}}
}
2. IO多路复用
通过上面的BIO代码我们可以看出,遍历文件描述符这个操作是用户态完成的,在每一次循环过程中,我们都需要对每个fd进行一次系统调用,当我们有100个fd时,每次遍历文件描述符就需要100次系统调用,在用户态到内核态进行切换是很耗费资源的。
那么用户态能解决这个事情吗?肯定是不行的,因此从上个实际80年代开始,unix就开始逐渐提供select, poll, epoll等机制,在内核态去遍历文件描述符。这三个机制实现细节有些差异,但是整体流程都是:用户态接受到文件描述符,将文件描述符的列表fds交给内核态,进行系统调用,内核态完成文件描述符的遍历,将数据准备就绪的文件描述符返回给用户态。因此,一次遍历从之前的100次系统调用就减少为1次系统调用。
因此IO多路复用,复用的是什么?复用的实际上是系统调用,从之前的一次系统调用判断一个文件描述符,变成了一次系统调用判断整个文件描述符列表。
Reactor
这部分内容较多,详见下一篇文章
