【Python实战因果推断】4_因果效应异质性4
目录
Cumulative Gain
Target Transformation
Cumulative Gain
如果采用与累积效应曲线完全相同的逻辑，但将每个点乘以累积样本 Ncum/N，就会得到累积增益曲线。现在，即使曲线的起点具有最高的效果（对于一个好的模型来说），它也会因为相对规模较小而缩小。看一下代码，变化在于我现在每次迭代都会将效果乘以（行/大小）。此外，我还可以选择按 ATE 对曲线进行归一化处理，这就是为什么我还要在每次迭代时从效果中减去归一化处理的原因：
def cumulative_gain_curve(df, prediction, y, t,ascending=False, normalize=False, steps=100):effect_fn = effect(t=t, y=y)normalizer = effect_fn(df) if normalize else 0size = len(df)ordered_df = (df.sort_values(prediction, ascending=ascending).reset_index(drop=True))steps = np.linspace(size/steps, size, steps).round(0)effects = [(effect_fn(ordered_df.query(f"index<={row}"))-normalizer)*(row/size)for row in steps]return np.array([0] + effects)cumulative_gain_curve(test_pred, "cate_pred", "sales", "discounts")如果您不想费心实现所有这些函数，可以使用Python库为您处理这些问题。您可以简单地从fklearn因果模块中导入所有曲线及其AUC
from fklearn.causal.validation.auc import *
from fklearn.causal.validation.curves import *三种模型的累积增益和归一化累积增益如下图所示。在这里，CATE 排序较好的模型是曲线与代表 ATE 的虚线之间面积最大的模型：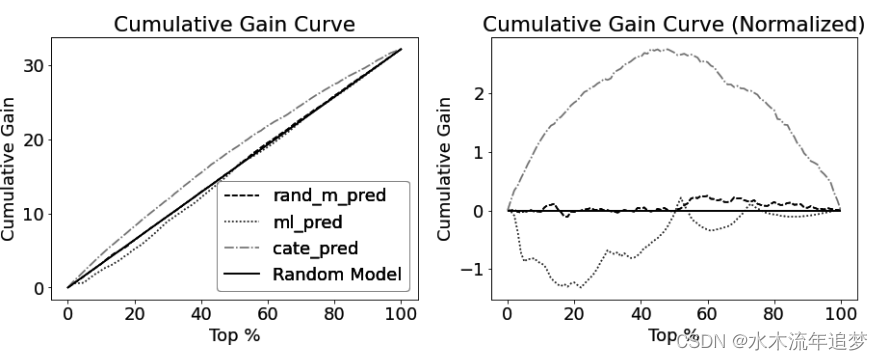
要将模型性能总结为一个数字，只需将归一化累积增益曲线上的数值相加即可。就 CATE 排序而言，数值最大的模型将是最佳模型。下面是您目前评估的三个模型的曲线下面积（AUC）。请注意，ML 模型的面积为负值，因为它对 CATE 进行了反向排序：
同样，您可以将模型的性能浓缩为一个数字，这一点也非常了不起，因为它可以自动选择模型。不过，虽然我很喜欢最后这条曲线，但在使用时还是需要注意一些问题。首先，在你看到的所有曲线中，重要的是要记住曲线中的每个点都是一个估计值，而不是地面真实值。它是对某一特定群体--有时是非常小的群体--的回归斜率的估计值。既然是回归估计值，它就取决于 T 和 Y 之间的关系是否正确。即使是随机化，如果治疗与干预结果之间的关系是一个对数函数，那么将效果估计为一条直线就会得出错误的结果。如果知道干预反应函数的形状，就可以将效应函数调整为 y~log(t) 的斜率，而不是 y~t。但要做到这一点，您需要知道正确的形状。
其次，这些曲线并不真正关心你是否正确地计算了 CATE。它们只关心排序是否正确。例如，如果您将任何一个模型的预测值减去-1,000，它们的累积增益曲线将保持不变。因此，即使您对 CATE 的估计存在偏差，这种偏差也不会在这些曲线中显示出来。现在，如果您只关心干预的优先次序，这可能不是问题。在这种情况下，排序就足够了。但是，如果您关心的是如何精确估算 CATE，那么这些曲线可能会误导您。如果您有数据科学背景，您可以将累积增益曲线与 ROC 曲线相提并论。同样，具有良好 ROC-AUC 的模型并不一定经过校准。
第三，或许也是最重要的一点，上述所有方法都需要无偏差数据。如果存在任何偏差，你对分组或 ATE 的效果估计都将是错误的。如果干预不是随机的，从理论上讲，你仍然可以使用这些评估技术，前提是你之前通过使用 IPW 的正交化等方法对数据进行了去偏差处理。不过，我对此有点怀疑。相反，我强烈建议你投资一些实验数据，哪怕只是一点点，只用于评估目的。这样，您就可以专注于效应异质性，而不必担心混杂因素的悄然出现。
因果模型评估是一个仍在发展中的研究领域。因此，它仍有许多盲点。例如，目前展示的曲线只能告诉您一个模型在 CATE 排序方面有多好。我还没有找到一个很好的解决方案来检查您的模型是否能正确预测 CATE。我喜欢做的一件事是在使用累积增益曲线的同时使用量子效应曲线图，因为前者能让我了解模型的校准程度，后者能让我了解模型对 CATE 的排序情况。至于归一化累积增益，它只是一个使可视化更容易的放大图。但我承认这并不理想。如果你正在寻找像 R2 或 MSE 这样的总结性指标--它们都是预测模型中常用的指标--我很遗憾地告诉你，在因果建模领域我还没有找到与它们类似的指标。不过，我还是找到了目标转换。
Target Transformation
X = ["C(month)", "C(weekday)", "is_holiday", "competitors_price"]y_res = smf.ols(f"sales ~ {'+'.join(X)}", data=test).fit().residt_res = smf.ols(f"discounts ~ {'+'.join(X)}", data=test).fit().residtau_hat = y_res/t_res接下来，您可以使用它来计算所有模型的MSE。注意我也如何使用前面讨论的权重：
from sklearn.metrics import mean_squared_errorfor m in ["rand_m_pred", "ml_pred", "cate_pred"]:wmse = mean_squared_error(tau_hat, test_pred[m],sample_weight=t_res**2)print(f"MSE for {m}:", wmse)根据这个加权MSE，再次，用于估计CATE的回归模型比其他两个表现更好。还有，这里还有一些有趣的东西。ML模型的性能比随机模型要差。这并不奇怪，因为ML模型试图预测Y，而不是τi。
只有当效应与结果相关时，预测 Y 才能很好地对 τi 进行排序或预测。这种情况一般不会发生，但在某些情况下可能会发生。其中有些情况在商业中相当常见，因此值得一探究竟。