状态压缩DP——AcWing 327. 玉米田
状态压缩DP
定义
状态压缩 DP 是一种通过二进制压缩状态的动态规划算法。它通过使用位运算来加速状态的转移和计算,从而提高算法的效率。
注意事项
- 数据范围:状态压缩 DP 通常适用于数据范围较小的问题,因为它需要使用二进制来表示状态,所以状态数量会随着数据范围的增加而呈指数级增长。
- 位运算:位运算在状态压缩 DP 中非常常用,需要熟练掌握位运算的基本操作,如与、或、异或、左移、右移等。
- 状态表示:选择合适的状态表示方式非常重要,需要根据问题的特点和要求来设计状态。一般来说,可以使用二进制数来表示状态,其中每一位表示一个元素的选择情况。
- 状态转移:状态转移是状态压缩 DP 的核心,需要根据问题的逻辑来设计状态转移方程。在状态转移过程中,需要注意边界情况和特殊情况的处理。
- 初始化:正确的初始化状态非常重要,需要根据问题的要求来初始化状态。一般来说,可以将初始状态设置为全 0 或全 1。
- 空间复杂度:状态压缩 DP 通常需要使用较大的空间来存储状态,因此需要注意空间复杂度的控制。可以通过滚动数组、压缩状态等方式来减少空间的使用。
解题思路
- 确定状态:根据问题的要求,确定需要使用的状态。状态可以是一个整数、一个二进制数或一个数组等。
- 设计状态转移方程:根据问题的逻辑,设计状态转移方程。状态转移方程描述了从一个状态到另一个状态的转移方式。
- 初始化状态:根据问题的要求,初始化状态。初始化状态通常是一个边界情况或特殊情况。
- 进行状态转移:使用状态转移方程,从初始状态开始,逐步进行状态转移,计算出每个状态的值。
- 输出结果:根据问题的要求,输出最终的结果。
状态压缩 DP 解决背包问题的一般步骤
- 确定状态:使用二进制数来表示背包的状态,每个物品的选择情况用一位二进制位表示,1 表示选择该物品,0 表示不选择。
- 设计状态转移方程:根据背包问题的逻辑,确定状态之间的转移关系。通常,状态转移方程会涉及到当前状态、上一个状态以及物品的选择情况。
- 初始化状态:根据问题的要求,初始化状态。通常,初始状态为全 0 或全 1。
- 进行状态转移:使用状态转移方程,从初始状态开始,逐步进行状态转移,计算出每个状态的值。
- 输出结果:根据问题的要求,输出最终的结果。
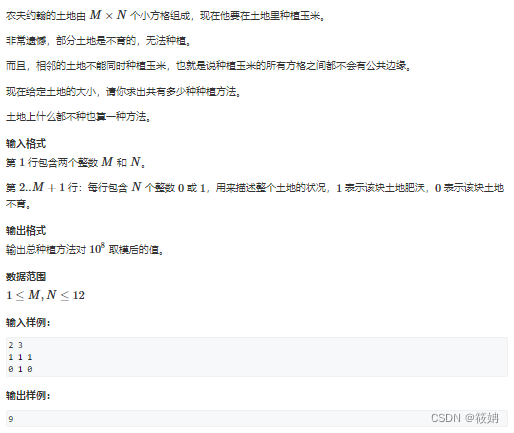
AcWing 327. 玉米田
题目描述
327. 玉米田 - AcWing题库
运行代码
#include <iostream>
#include <vector>
using namespace std;
const int N = 14, M = 1 << 12, mod = 1e8;
int n, m;
int w[N];
vector<int> state;
vector<int> head[M];
int f[N][M];
bool check(int x)
{return !(x & x << 1);
}
int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++)for(int j = 0; j < m; j ++){int t;cin >> t;w[i] += !t << j;}for(int i = 0; i < 1 << m; i ++)if(check(i)) state.push_back(i);for(int i = 0; i < state.size(); i ++)for(int j = 0; j < state.size(); j ++){int a = state[i], b = state[j];if(!(a & b)) head[i].push_back(j);}f[0][0] = 1; for(int i = 1; i <= n + 1; i ++)for(int j = 0; j < state.size(); j ++)if(!(state[j] & w[i]))for(auto k : head[j])f[i][j] = (f[i][j] + f[i - 1][k]) % mod;cout << f[n + 1][0] << endl;return 0;
}#include <iostream>
#include <vector>
using namespace std;
const int N = 14, M = 1 << 12, mod = 1e8;
int n, m;
int w[N];
vector<int> state;
vector<int> head[M];
int f[N][M];
bool check(int x)
{return !(x & x << 1);
}
int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++)for(int j = 0; j < m; j ++){int t;cin >> t;w[i] += !t << j;}for(int i = 0; i < 1 << m; i ++)if(check(i)) state.push_back(i);for(int i = 0; i < state.size(); i ++)for(int j = 0; j < state.size(); j ++){int a = state[i], b = state[j];if(!(a & b)) head[i].push_back(j);}f[0][0] = 1; for(int i = 1; i <= n + 1; i ++)for(int j = 0; j < state.size(); j ++)if(!(state[j] & w[i]))for(auto k : head[j])f[i][j] = (f[i][j] + f[i - 1][k]) % mod;cout << f[n + 1][0] << endl;return 0;
}代码思路
- 首先读入行数
n和列数m以及土地的状况,将不可种植的情况转化为一个整数表示。 - 通过
check函数判断一个状态是否满足相邻位没有同时为 1 的条件,将满足条件的状态存入state向量。 - 构建状态之间的关联关系,将没有冲突的状态对存入
head数组。 - 然后通过动态规划,从第一行开始逐步计算每个状态下的种植方法数,利用之前的状态和关联关系进行递推。
改进思路
- 可以考虑对一些重复的计算进行缓存或优化,提高效率。
- 代码的结构和逻辑可以进一步整理和优化,增强可读性。
改进代码
#include <iostream>
#include <vector>
using namespace std;
const int N = 14, M = 1 << 12, mod = 1e8;int n, m;
int w[N];
vector<int> state;
vector<int> head[M];
int f[N][M];bool check(int x) {return!(x & x << 1);
}void init() {for(int i = 0; i < 1 << m; i ++)if(check(i)) state.push_back(i);for(int i = 0; i < state.size(); i ++)for(int j = 0; j < state.size(); j ++) {int a = state[i], b = state[j];if(!(a & b)) head[i].push_back(j);}
}int main() {cin >> n >> m;for(int i = 1; i <= n; i ++)for(int j = 0; j < m; j ++) {int t;cin >> t;w[i] +=!t << j;}init();f[0][0] = 1; for(int i = 1; i <= n + 1; i ++)for(int j = 0; j < state.size(); j ++)if(!(state[j] & w[i]))for(auto k : head[j])f[i][j] = (f[i][j] + f[i - 1][k]) % mod;cout << f[n + 1][0] << endl;return 0;
}