Studying-代码随想录训练营day15| 222.完全二叉树的节点个数、110.平衡二叉树、257.二叉树的所有路径、404.左叶子之和
第十五天,二叉树part03💪,编程语言:C++
目录
257.完全二叉树的节点个数
110.平衡二叉树
257.二叉树的所有路径
404.左叶子之和
总结
257.完全二叉树的节点个数
文档讲解:代码随想录完全二叉树的节点个数
视频讲解:手撕完全二叉树的节点个数
题目:
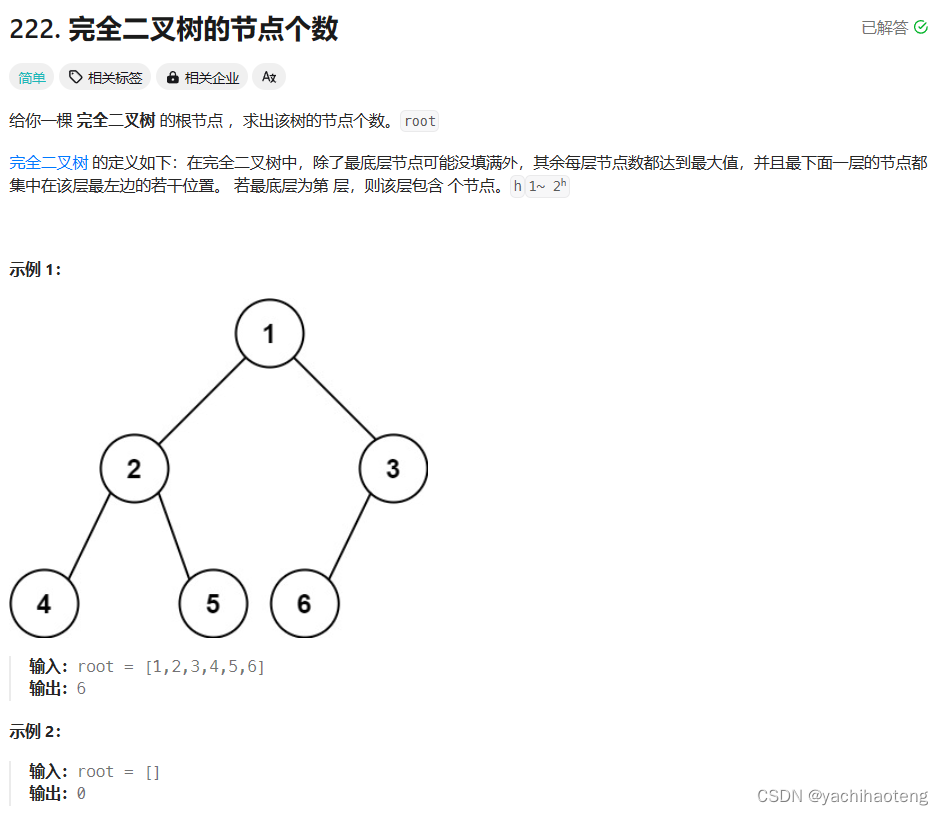
学习:
1. 根据完全二叉树的定义,我们可以把二叉树分为一个个满二叉树。满二叉树的定义为除叶子节点外,其余节点均含有左右两个孩子,此时节点的个数为2^height - 1;height就是这个满二叉树的高度。
2. 那如何确定是否是满二叉树呢,本题我们可以借助完全二叉树的定义,由于完全二叉树的特点,一个节点一定会先有它的左孩子,再有它的右孩子。因此倘若一棵树的一直往左遍历的深度,与一直往右遍历的深度相同,则说明这是一颗满二叉树,因为中间的节点一定是填满的,否则往右的深度一定时小于往左的深度。
3. 确定以上两点后,如何把一个二叉树分为一个个满二叉树。本题我们可以采用后序遍历的方法,在向下移动的过程中,我们可以每次判断该节点是否为一棵满二叉树的根节点(采用的方式就是2中所说的判断向左和向右的深度是否一样),如果是则可以通过满二叉树的式子直接返回该树的节点数,如果不是则继续往下。注意叶子节点在这也被我们看作成了一颗满二叉树,高度为1,节点个数为1。
代码:
//时间复杂度O(logn*logn)
//空间复杂度O(logn)
class Solution {
public:int countNodes(TreeNode* root) {//根节点为空,返回0//终止条件if (root == nullptr) return 0;TreeNode* left = root->left;TreeNode* right = root->right;int leftheight = 0; int rightheight = 0;while(left) {leftheight++;left = left->left;}while(right) {rightheight++;right = right->right;}//如果两边深度一样,则说明是一个完全二叉树,完全二叉树的节点数量为2^(leftheight + 1) - 1 if (leftheight == rightheight) return (2 << leftheight) - 1;//不满足终止条件的话,进入递归循环int leftnum = countNodes(root->left); //遍历左子树int rightnum = countNodes(root->right); //遍历右子树return 1 + leftnum + rightnum;}
};注意:本题也可以采用普通二叉树求节点数量的方式,采用层次遍历,时间复杂度为O(n)。
110.平衡二叉树
文档讲解:代码随想录平衡二叉树
视频讲解:手撕平衡二叉树
题目:
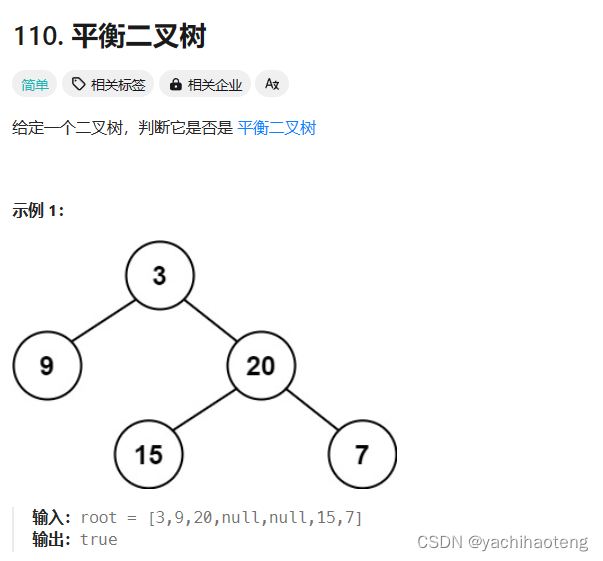
学习:平衡二叉树指的是,任意一个节点的左右子树的高度差不大于1。依据这个特点,我们可以采取后序遍历的方式,遍历每一个子树的高度,并且当存在一个子树的高度差大于2时,就可以立刻返回-1,不用继续遍历下去。
代码:
//时间复杂度O(n)
//空间复杂度O(n)
class Solution {
public://1.确定返回值,参数列表。//返回值:由于递归过程中需要比较左右子树的高度,所有返回值应该为int//参数:比较根节点左右子树的高度,因此只需要传入根节点即可int Height(TreeNode* root) {//2.确定终止条件、单层递归逻辑//①如果根节点为空,返回长度为0if (root == nullptr) return 0;//②如果已得知左子树不平衡,返回-1;int leftheight = Height(root->left);if (leftheight == -1) return -1;//③如果已得知右子树不平衡,返回-1;int rightheight = Height(root->right);if (rightheight == -1) return -1;return abs(leftheight - rightheight) > 1 ? -1 : (1 + max(leftheight, rightheight));} bool isBalanced(TreeNode* root) {if (Height(root) == -1) return false;return true;}
};注意:
- 此题不适合使用前序遍历,前序遍历一般用于求树的深度,是自顶向下的过程。 因此每次比较一个子树的深度时都需要遍历所有的子节点,时间复杂度会达到O(n^2)。后序遍历则不同,是自底向上的过程,在遍历的过程中,从底部开始比较,并把比较的结果不断往上传递,因此只需要遍历一遍节点即可。
- 此题也不适合使用迭代的方式,本题存在回溯比较的过程,使用迭代法会使得代码很复杂,且不利于实现回溯的过程,虽然递归一般来说都能用迭代来实现,但是也需要分析使用的场景。
257.二叉树的所有路径
文档讲解:二叉树的所有路径
视频讲解:手撕二叉树的所有路径
题目:
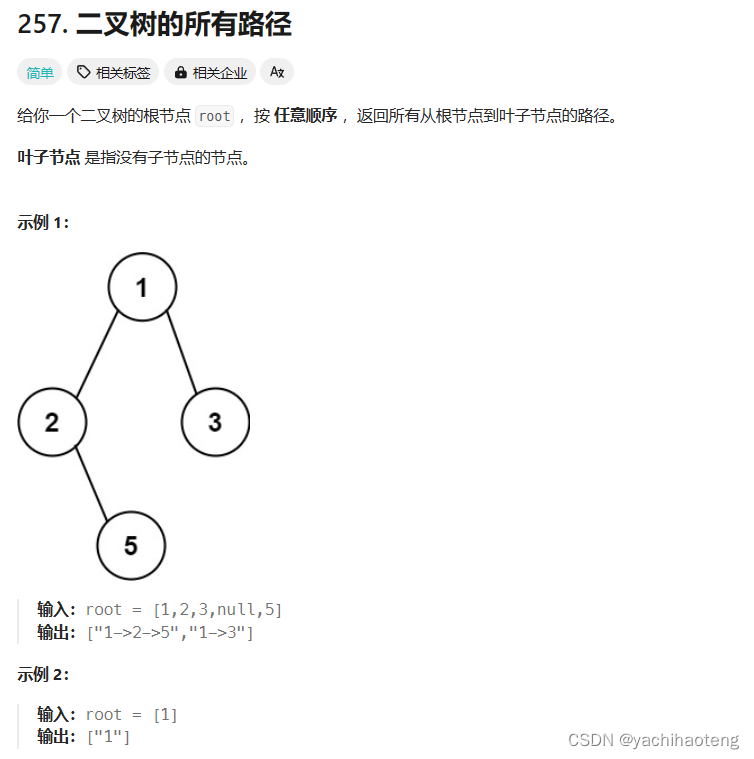
学习:
1. 本题要找到所有路径,因此必定需要遍历所有的节点,同时每条路径都是从根节点开始的,因此显然本题适合采用前序遍历来进行节点的遍历,遍历到下一个节点的时候,其父节点的信息就已经载入。
2. 同时本题存在大量的回溯过程,即找到一条路径后,要回到一个拐点(中间节点),再去寻找另一条路路径。回溯是下一章节的重点内容,其主要的实现方式就是递归实现,因此本题采用前序遍历的递归形式。
3. 本题在递归上有两个主要注意的点:①本题终止条件不再是找到空节点,而是找到叶子节点这条路径就可以终止了;②本题采用前序遍历,但是对节点的处理要放在终止条件判断前,因为每遍历到一个节点就需要把它加入到字符串当中。
代码:
//时间复杂度O(n^2)
//空间复杂度O(n^2)
class Solution {
public://注意path不能使用引用的方式,这种赋值的方式,不会改变传进来的值,因此会实现自动回溯void traversal(TreeNode* cur, string path, vector<string>& result) {path += to_string(cur->val); // 中,中为什么写在这里,因为最后一个节点也要加入到path中path += "->";if(cur->left == nullptr && cur->right == nullptr) {//把最后多余的箭头pop()掉path.pop_back();path.pop_back();result.push_back(path);}if(cur->left) { //左traversal(cur->left, path, result);}if(cur->right) { //右traversal(cur->right, path, result);}}vector<string> binaryTreePaths(TreeNode* root) {vector<string> result;traversal(root, "", result);return result;}
};注意:上面是使用了拷贝构造string path的方式,每一个递归拷贝了自己的一份path,以此来实现回溯过程。但也能够使用引用的方式,大家公用一份数组,但要注意此时需要自己进行回溯。
class Solution {
private:void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) {path.push_back(cur->val); // 中,中为什么写在这里,因为最后一个节点也要加入到path中 // 这才到了叶子节点if (cur->left == NULL && cur->right == NULL) {string sPath;for (int i = 0; i < path.size() - 1; i++) {sPath += to_string(path[i]);sPath += "->";}sPath += to_string(path[path.size() - 1]);result.push_back(sPath);return;}if (cur->left) { // 左 traversal(cur->left, path, result);path.pop_back(); // 回溯}if (cur->right) { // 右traversal(cur->right, path, result);path.pop_back(); // 回溯}}public:vector<string> binaryTreePaths(TreeNode* root) {vector<string> result;vector<int> path;if (root == NULL) return result;traversal(root, path, result);return result;}
};总结:回溯的过程,实际上就是把上一个循环的所有数据环境保存下来,再回到上一个循环的时候,保证环境不变的过程。可以通过把递归放入栈中,体会回溯。
404.左叶子之和
文档讲解:代码随想录左叶子之和
视频讲解:手撕左叶子之和
题目:
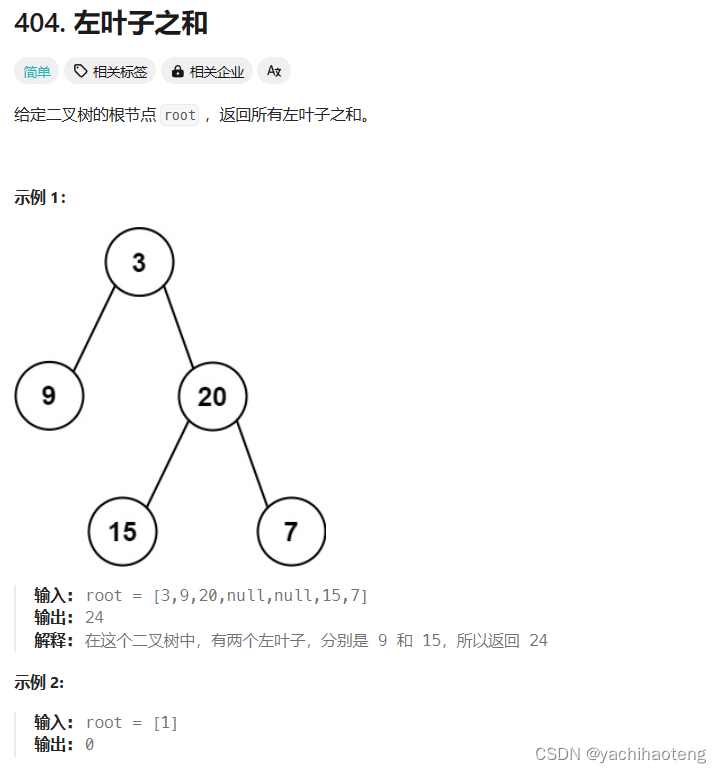
学习:本题需要找到所有的左叶子节点。左叶子节点的特点:1.是叶子节点,2.是父节点的左孩子。根据这两个特点来进行递归构造。
代码:前序遍历(递归)
//时间复杂度O(n)
//空间复杂度O(n)
class Solution {
public:// 1.确定返回值和参数列表,这里我们使用一个sum来计算总和,因此不需要返回值。void sumLeft(int& sum, TreeNode* root) {//左叶子节点的定义,1.是父节点的左节点,2.是叶子节点//2.确定终止条件if(root == nullptr) return;//其实这个也可以不写,如果不写不影响结果,但就会让递归多进行了一层。if(root->left == nullptr && root->right == nullptr) return;//3.确定单层递归逻辑//找到左叶子节点的父节点if(root->left != nullptr && root->left->left == nullptr && root->left->right == nullptr) {sum += root->left->val;}//如果没找到左叶子节点的父节点,则向下遍历sumLeft(sum, root->left);sumLeft(sum, root->right);}int sumOfLeftLeaves(TreeNode* root) {int sum = 0;sumLeft(sum, root);return sum;}
};注意:本题也可以采用后序遍历的方式。采用后序的遍历,返回值设为int型,从底部开始把左叶子节点的值累加并传递给父节点。
class Solution {
public:int sumOfLeftLeaves(TreeNode* root) {if (root == NULL) return 0;if (root->left == NULL && root->right== NULL) return 0;int leftValue = sumOfLeftLeaves(root->left); // 左if (root->left && !root->left->left && !root->left->right) { // 左子树就是一个左叶子的情况leftValue = root->left->val;}int rightValue = sumOfLeftLeaves(root->right); // 右int sum = leftValue + rightValue; // 中return sum;}
};
总结
今天的题重在对递归的使用,和对递归三大条件的设计上。
- 完全二叉树的节点个数:通过对递归条件终止条件的特殊处理,讲时间复杂度下降。
- 平衡二叉树:重点在于后序遍历求得树的高度,前序遍历求得树的深度,要根据需求进行选择。
- 二叉树的所有路径:重点在于对回溯的理解,要找到所有的路径,需要保存父节点的信息。同时由于每个节点遍历的时候就需要立马加入路径队列,因此还需要把对节点的处理放在终止条件的判断前。
- 左叶子之和:有两种不同的方法,根据左叶子节点的特点构造递归三部曲。
