【机器学习】线性回归:从基础到实践的深度解析


🌈个人主页: 鑫宝Code
🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础
💫个人格言: "如无必要,勿增实体"

文章目录
- 线性回归:从基础到实践的深度解析
- 引言
- 一、线性回归基础
- 1.1 定义与目的
- 1.2 简单线性回归
- 1.3 多元线性回归
- 二、数学原理
- 2.1 最小二乘法
- 2.2 模型评估
- 三、实现方法
- 3.1 手动实现
- 3.2 利用库函数
- 四、实际应用中的考虑
- 4.1 特征选择与工程
- 4.2 正则化
- 4.3 模型评估与调优
- 五、总结与展望
线性回归:从基础到实践的深度解析

引言
线性回归作为统计学习和机器学习领域的基石之一,自19世纪末由Francis Galton和Carl Pearson提出以来,一直是数据分析、预测建模不可或缺的工具。它通过建立输入特征与连续目标变量之间的线性关系模型,为我们提供了一种理解和预测世界现象的强大手段。本文将深入浅出地介绍线性回归的基本概念、数学原理、实现方法以及在实际应用中的注意事项,力求为读者构建一个全面而深刻的理解框架。
一、线性回归基础
1.1 定义与目的
线性回归(Linear Regression)是一种预测分析模型,其基本思想是利用一个或多个自变量(输入特征)来预测或解释一个连续型因变量(目标变量)。简而言之,线性回归试图找到一个最佳拟合直线(或多维空间中的超平面),使得所有数据点到该直线的偏差平方和最小。
1.2 简单线性回归
简单线性回归是最基础的形式,仅涉及一个自变量 x x x和一个因变量 y y y。其模型可以表示为:
y = β 0 + β 1 x + ϵ y = \beta_0 + \beta_1x + \epsilon y=β0+β1x+ϵ
其中, β 0 \beta_0 β0是截距项, β 1 \beta_1 β1是斜率, ϵ \epsilon ϵ是误差项,反映了数据中的随机波动。
1.3 多元线性回归
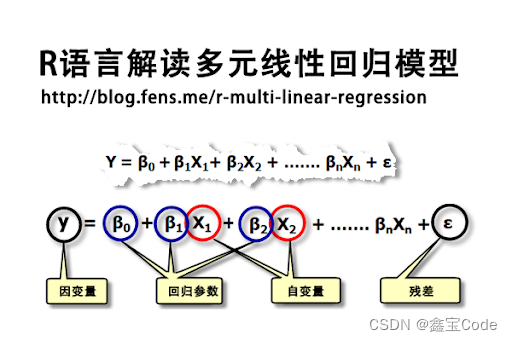
当存在两个或更多自变量时,模型扩展为多元线性回归:
y = β 0 + β 1 x 1 + β 2 x 2 + . . . + β n x n + ϵ y = \beta_0 + \beta_1x_1 + \beta_2x_2 + ... + \beta_nx_n + \epsilon y=β0+β1x1+β2x2+...+βnxn+ϵ
这里, x 1 , x 2 , . . . , x n x_1, x_2, ..., x_n x1,x2,...,xn代表多个自变量, β 1 , β 2 , . . . , β n \beta_1, \beta_2, ..., \beta_n β1,β2,...,βn是各自变量的系数。
二、数学原理
2.1 最小二乘法
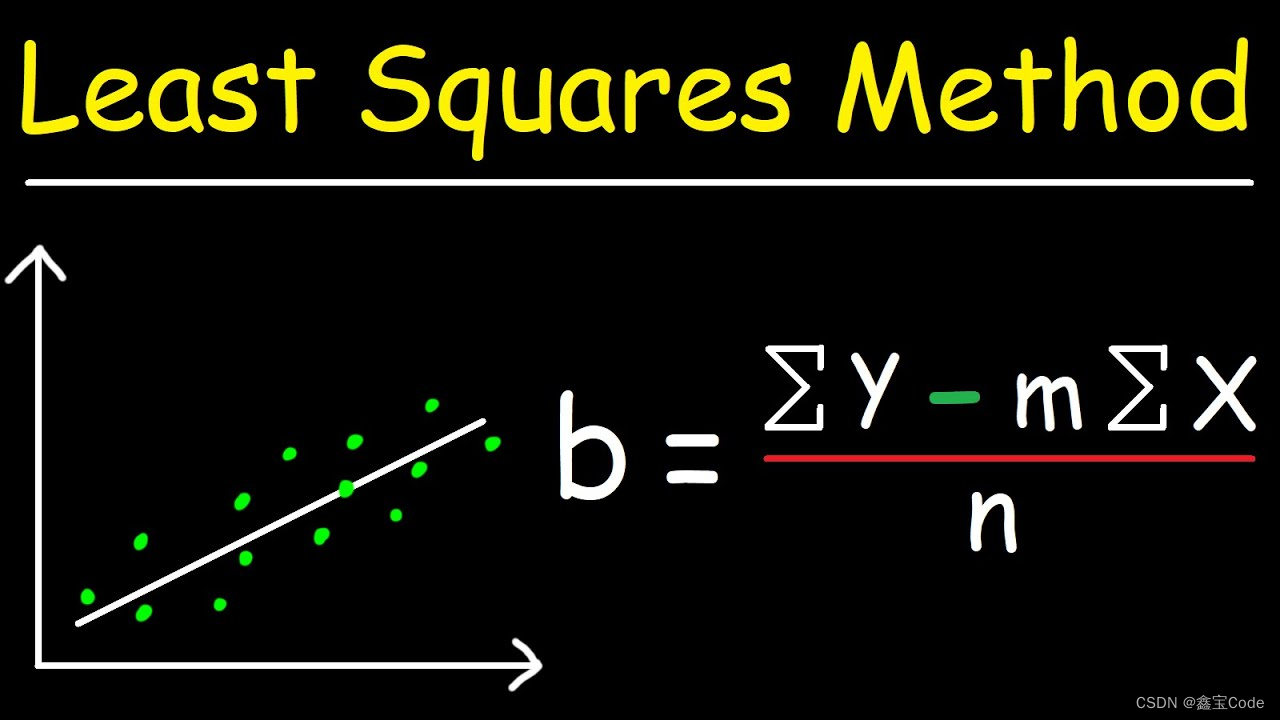
最小二乘法是线性回归中常用的参数估计方法。其核心思想是通过最小化残差平方和(RSS: Residual Sum of Squares)来确定模型参数:
RSS = ∑ i = 1 n ( y i − ( β 0 + β 1 x i 1 + . . . + β n x i n ) ) 2 \text{RSS} = \sum_{i=1}^{n}(y_i - (\beta_0 + \beta_1x_{i1} + ... + \beta_nx_{in}))^2 RSS=i=1∑n(yi−(β0+β1xi1+...+βnxin))2
通过求导数并令导数等于零,可以解得参数 β 0 , β 1 , . . . , β n \beta_0, \beta_1, ..., \beta_n β0,β1,...,βn的最优值。
2.2 模型评估
- 均方误差(MSE):衡量预测值与真实值之间差异的平均程度。
- 决定系数(R²):表示模型解释的变异量占总变异量的比例,值越接近1说明模型拟合度越高。
三、实现方法
3.1 手动实现
手动实现线性回归包括数据预处理、梯度下降或正规方程求解等步骤。以梯度下降为例,迭代更新参数直到收敛:
β j : = β j − α ∂ ∂ β j RSS \beta_j := \beta_j - \alpha \frac{\partial}{\partial \beta_j}\text{RSS} βj:=βj−α∂βj∂RSS
其中, α \alpha α是学习率,控制每次迭代的步长。
3.2 利用库函数
在Python中,可以使用scikit-learn库轻松实现线性回归:
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train, y_train)
predictions = model.predict(X_test)
四、实际应用中的考虑
4.1 特征选择与工程
- 相关性分析:筛选与目标变量高度相关的特征。
- 多项式特征:对非线性关系进行转换,增强模型表达能力。
4.2 正则化
- L1正则化(Lasso回归):倾向于产生稀疏解,可用于特征选择。
- L2正则化(Ridge回归):减少模型复杂度,避免过拟合。

4.3 模型评估与调优
- 交叉验证:确保模型泛化性能。
- 网格搜索:自动寻找最佳超参数组合。
五、总结与展望
线性回归以其简单直观、易于理解和实现的特点,在金融、医疗、社会科学等多个领域发挥着重要作用。然而,面对复杂的数据关系,非线性模型如支持向量机、神经网络等可能提供更好的解决方案。未来,结合深度学习技术的线性回归变体,以及在大数据环境下的高效实现,将继续推动这一经典模型的发展,拓展其应用边界。
通过本文的介绍,希望能帮助读者建立起线性回归的坚实理论基础,并激发进一步探索和应用的兴趣。随着技术的不断进步,线性回归及其衍生方法将持续为解决实际问题提供强大的支持。


