当前位置：首页 > news >正文

算法day29

news 2025/8/15 6:26:30

第一题

695. 岛屿的最大面积

本题解法：采用bfs的算法；

本题使用象限数组的遍历方法和定义布尔数组vis来遍历每一个元素的上下左右元素，防治被遍历的元素被二次遍历；

本题具体分析如上题故事，但是由于要求区域的最大面积，所以在bfs方法中找到合适的元素进行入队列操作时，我们要对其个数进行统计；

至此，代码如下：
class Solution {//象限坐标数组int[] dx = {0,0,1,-1};int[] dy = {1,-1,0,0};boolean[][] vis = new boolean[51][51];int m,n;public int maxAreaOfIsland(int[][] grid) {m = grid.length;n = grid[0].length;int ret = 0;//统计最大面积for(int i = 0;i < m ;i++){for(int j = 0;j < n ;j++){if(grid[i][j] == 1 && !vis[i][j]){ret = Math.max(ret,bfs(grid,i,j));}}}return ret;}public int bfs(int[][] grid,int i,int j){int cot = 0;Queue<int[]> q = new LinkedList<>();q.add(new int[]{i,j});vis[i][j] = true;cot++;while(!q.isEmpty()){int[] t = q.poll();int a = t[0],b = t[1];for(int s = 0;s < 4;s++){int x = a +dx[s],y = b + dy[s];if(x >= 0 && x <m && y >= 0 && y < n && grid[x][y] == 1 && !vis[x][y]){q.add(new int[]{x,y});vis[x][y] = true;cot++;}}       }return cot;}
}

第二题

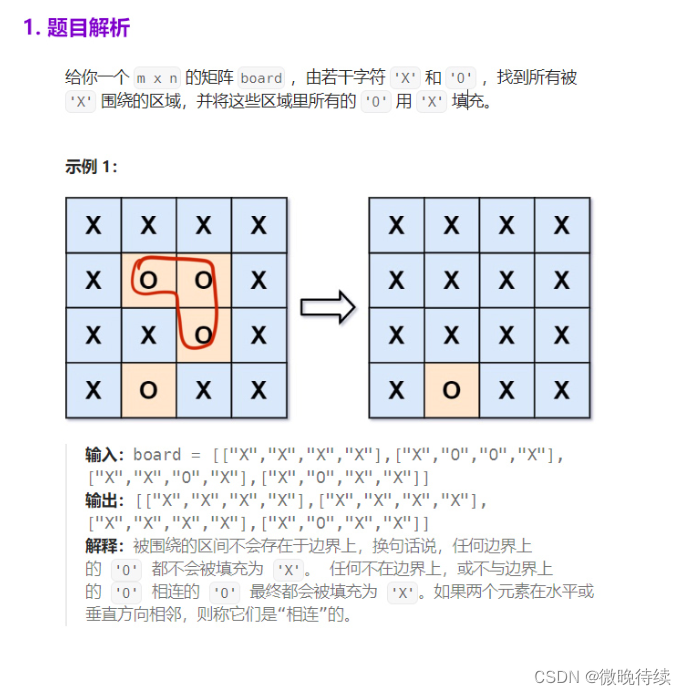
130. 被围绕的区域

解法：bfs层序遍历

解题步骤如下：

步骤一：

如上图所示，首先遍历第一行，最后一行，第一列，最后一列的元素，查找与其相邻的元素，并将这些元素o变成符号*；

步骤二：

遍历整个图像中所有的元素，遇到的o字符变成x字符，遇到的*字符变成o字符，如此满足题意；

至此，代码如下：

class Solution {//象限坐标数组int[] dx = {0,0,1,-1};int[] dy = {1,-1,0,0};int m,n;public void solve(char[][] board) {m = board.length;n = board[0].length;//1、先处理边界的0，全部修改成*//修改第一行和最后一行for(int j = 0;j < n;j++){if(board[0][j] == 'O' ) bfs(board,0,j);if(board[m-1][j] == 'O' ) bfs(board,m-1,j);}//修改第一列和最后一列for(int i = 0;i < m;i++){if(board[i][0] == 'O' ) bfs(board,i,0);if(board[i][n-1] == 'O' ) bfs(board,i,n-1);}//2、还原，将剩下的0变成x，将边缘的*变为0for(int i = 0;i< m;i++){for(int j = 0;j < n ;j++){if(board[i][j] == 'O') board[i][j] = 'X';else if(board[i][j] == '*') board[i][j] = 'O';}}}public void bfs(char[][] board,int i,int j){Queue<int[]> q = new LinkedList<>();q.add(new int[]{i,j});board[i][j] = '*';while(!q.isEmpty()){int[] t = q.poll();int a = t[0],b = t[1];for(int s = 0;s < 4;s++){int x = a +dx[s],y = b + dy[s];if(x >= 0 && x <m && y >= 0 && y < n && board[x][y] == 'O' ){board[x][y] = '*';q.add(new int[]{x,y});}}       }}
}

第三题

1926. 迷宫中离入口最近的出口

本题的题目类型可以理解为边权为1的最短路问题；

迷宫游戏，其数据结构模拟：一个迷宫矩阵，当每一个二维坐标相对性的字符为+，则是路障，坐标对应的字符为.,则表示是可以前进的路，当前我们所在的位置就是一个二维坐标对应的坐标；

由于我们的安全出口的路线就是从给定的位置开始移动，移动到边界；且在所能到达安全出口的所有路线里面返回最短的路线（即最少的移动次数）

我们在遍历当前位置的上下左右合法位置的时候采用的象限数组的方法，同时由于移动之后我们不能原路返回，所以采用定义布尔数组vis，给每一个遍历过的位置在该数组里面定义为true，防治二次遍历；

我们将初识位置放于队列中，将该位置的上下左右位置都进行过遍历，每遍历到一个合法的位置，就将该位置放于队列中，且定义的统计移动次数的cot加一，当遍历到矩阵的边界时候，返回最短的cot变量；

至此，代码如下：
class Solution {//象限坐标数组int[] dx = {0,0,1,-1};int[] dy = {1,-1,0,0};public int nearestExit(char[][] maze, int[] entrance) {int m= maze.length,n = maze[0].length;boolean[][] vis = new boolean[m][n];Queue<int[]> q = new LinkedList<>();q.add(new int[]{entrance[0],entrance[1]});vis[entrance[0]][entrance[1]]  = true;int step = 0;while(!q.isEmpty()){step++;int sz = q.size();for(int i = 0;i < sz;i++){int[] t = q.poll();int a = t[0],b = t[1];for(int j = 0;j<4;j++){int x = a +dx[j],y = b + dy[j];if(x >= 0 && x <m && y >= 0 && y < n && maze[x][y] == '.' && !vis[x][y]){//判断是否已经走出出口if(x == 0|| x == m-1 || y == 0 || y == n-1) return step;q.add(new int[]{x,y});vis[x][y] = true;}}}}return -1;}
}