当前位置：首页 > news >正文

对称二叉树[简单]

news 2025/7/1 17:26:17

优质博文：IT-BLOG-CN
在这里插入图片描述

一、题目

给你一个二叉树的根节点root，检查它是否轴对称。

示例 1：

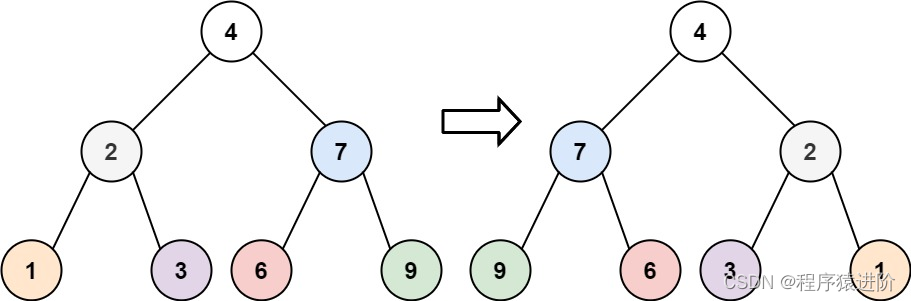
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

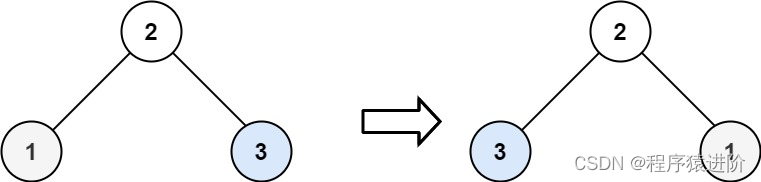
输入：root = [1,2,2,null,3,null,3]
输出：false

树中节点数目在范围[1, 1000]内
-100 <= Node.val <= 100

进阶： 你可以运用递归和迭代两种方法解决这个问题吗？

二、代码

【1】递归： 我们将一个树的左右节点相同，转换为两个根节点具有相同的值，每个树的右子树都与另一个树的左子树镜像对称。我们通过一个递归函数，通过同步移动两个指针的方式来遍历树，rootLeft和rootRight都指向一个树的根，然后rootLeft右移时，rootRight左移，rootLeft左移时，rootRight右移。检查rootLeft和rootRight的值是否相等，如果相等再判断左右子树是否对称。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public boolean isSymmetric(TreeNode root) {return check(root, root);}private boolean check(TreeNode rootLeft, TreeNode rootRight) {if (rootLeft == null && rootRight == null) {return true;}if (rootLeft == null || rootRight == null) {return false;}return rootLeft.val == rootRight.val && check(rootLeft.left, rootRight.right) && check(rootLeft.right, rootRight.left);}
}
**时间复杂度：** 这里遍历了这棵树，渐进时间复杂度为`O(n)`。  
**空间复杂度：** 这里的空间复杂度和递归使用的栈空间有关，这里递归层数不超过`n`，故渐进空间复杂度为`O(n)`。

【2】迭代： 我们引入一个队列，这是把递归程序改写成迭代程序的常用方法。初始化时我们把根节点入队两次。每次提取两个结点并比较它们的值（队列中每两个连续的结点应该是相等的，而且它们的子树互为镜像），然后将两个结点的左右子结点按相反的顺序插入队列中。当队列为空时，或者我们检测到树不对称（即从队列中取出两个不相等的连续结点）时，该算法结束。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public boolean isSymmetric(TreeNode root) {return check(root, root);}private boolean check(TreeNode rootLeft, TreeNode rootRight) {Queue<TreeNode> q = new LinkedList<TreeNode>();q.offer(rootLeft);q.offer(rootRight);while(!q.isEmpty()) {rootLeft = q.poll();rootRight = q.poll();if (rootLeft == null && rootRight == null) {continue;}if ((rootLeft == null || rootRight == null) || (rootLeft.val != rootRight.val)) {return false;}q.offer(rootLeft.left);q.offer(rootRight.right);q.offer(rootLeft.right);q.offer(rootRight.left);}return true;}
}

时间复杂度： 这里遍历了这棵树，渐进时间复杂度为O(n)。
空间复杂度： 这里需要用一个队列来维护节点，每个节点最多进队一次，出队一次，队列中最多不会超过n个点，故渐进空间复杂度为O(n)。

【3】对称二叉树定义： 对于树中任意两个对称节点L和R，一定有：
L.val = R.val ：即此两对称节点值相等。
L.left.val = R.right.val ：即L的左子节点和R的右子节点对称。
L.right.val = R.left.val ：即L的右子节点和R的左子节点对称。
根据以上规律，考虑从顶至底递归，判断每对左右节点是否对称，从而判断树是否为对称二叉树。

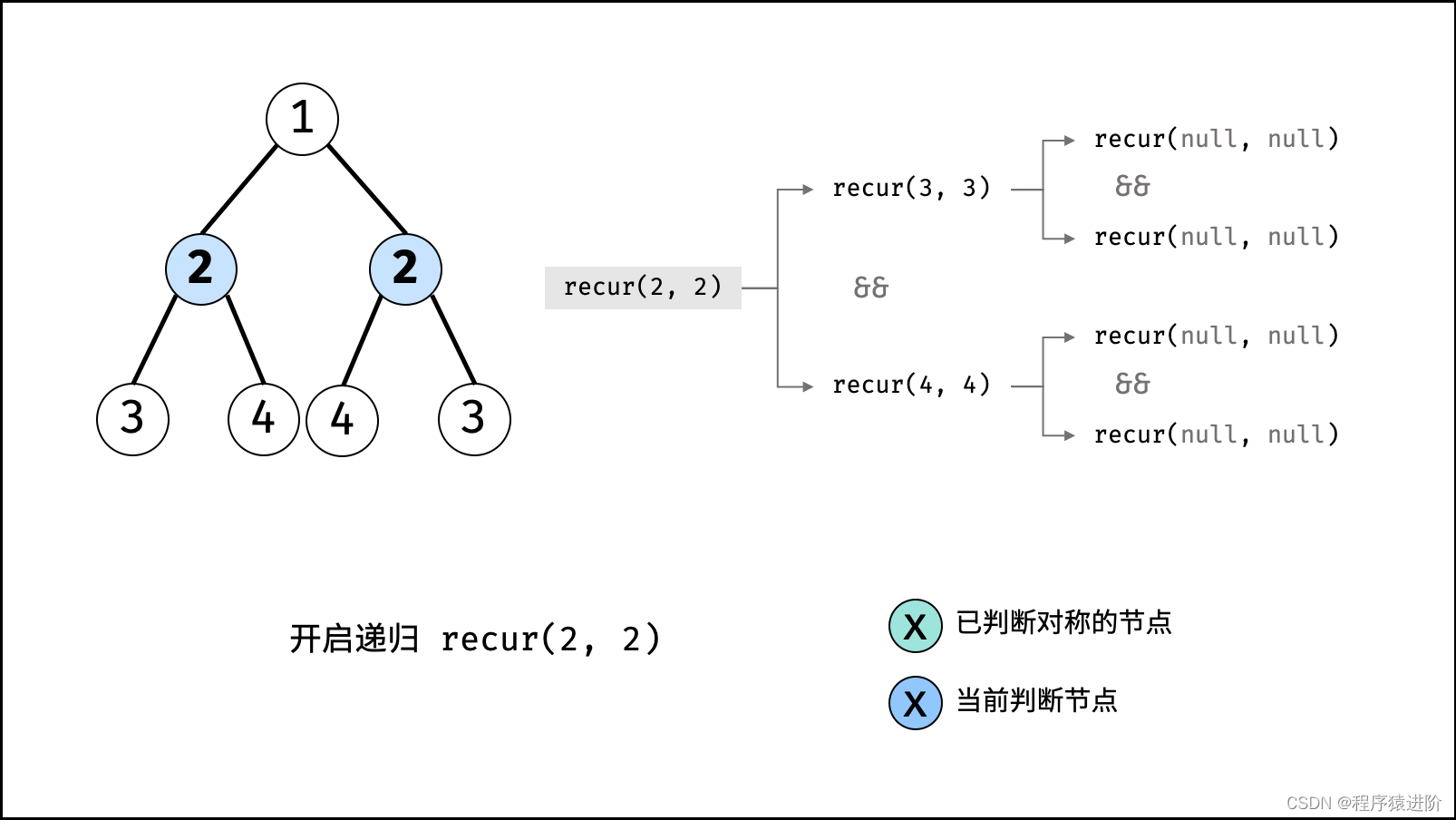
算法流程： 函数isSymmetric(root) ：
【1】特例处理：若根节点 root 为空，则直接返回 truetruetrue 。
【2】返回值：即 recur(root.left, root.right) ;

函数recur(L, R) ：
终止条件：
1、当 L 和 R 同时越过叶节点：此树从顶至底的节点都对称，因此返回 truetruetrue 。
2、当 L 或 R 中只有一个越过叶节点：此树不对称，因此返回 falsefalsefalse 。
3、当节点 L 值 ≠ 节点 R 值：此树不对称，因此返回 falsefalsefalse 。

递推工作：
1、判断两节点 L.left 和 R.right 是否对称，即 recur(L.left, R.right) 。
2、判断两节点 L.right 和 R.left 是否对称，即 recur(L.right, R.left) 。
3、返回值：两对节点都对称时，才是对称树，因此用与逻辑符 && 连接。
在这里插入图片描述

class Solution {public boolean isSymmetric(TreeNode root) {return root == null || recur(root.left, root.right);}boolean recur(TreeNode L, TreeNode R) {if (L == null && R == null) return true;if (L == null || R == null || L.val != R.val) return false;return recur(L.left, R.right) && recur(L.right, R.left);}
}

复杂度分析：
时间复杂度O(N) ： 其中N为二叉树的节点数量，每次执行recur()可以判断一对节点是否对称，因此最多调用N/2次recur()方法。
空间复杂度O(N) ： 如下图所示，最差情况下（二叉树退化为链表），系统使用O(N)大小的空间。
在这里插入图片描述