当前位置：首页 > news >正文

栈和队列详细讲解+算法动画

news 2025/6/21 7:06:42

栈和队列

栈stack

栈也是一种线性结构
相比数组，栈对应的操作数数组的子集
只能从一端添加元素，也只能从一端取出元素
这一端称为栈顶

栈是一种后进先出的数据结构
Last in Firt out(LIFO)
在计算机的世界里，栈拥有者不可思议的作用

栈的应用

无处不在的undo操作(撤销)
- 沉迷学习不法

程序调用的系统栈
- 从A函数调用B函数，B函数在调用C函数
- A2，表示进行到A函数的第二行

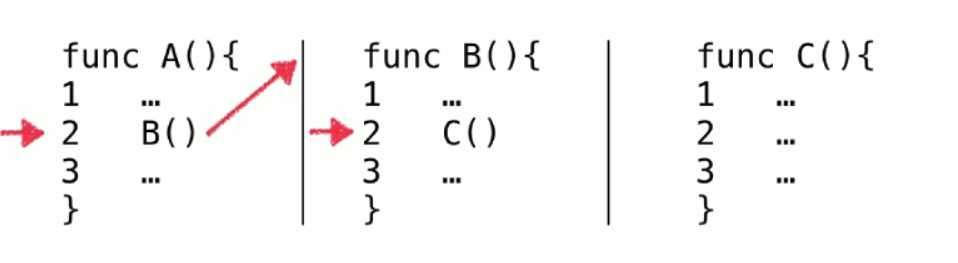
当一个子过程可以自动回到上层调用继续执行的原因，因为有系统栈去记录每一个中断的点。子过程的调用实现机理就是如此。对于递归的理解会在后续介绍。

栈的实现

Stack

void push(E)
E pop()
E peek()
int getSize()
boolean isEmpty()

从用户的角度看，支持这些操作就好

具体底层实现，用户不关心

实际底层有多种实现方式

采用多态的方式

public Interface Stack<E>{int getSize();boolean isEmpty();void push(E e);E pop();E peek();
}
public class ArrayStack<E> implements Stack<E>{Array<E> array;public ArrayStack(int getCapacity){array = new Array<>(capacity);}public ArrayStack(){array = new Array<>();}@Overrideint getSize(){return array.getSise;    }@Overrideboolean isEmpty(){return array.isEmpty();}@Overridepublic int getCapacity(){return array.getCapacity();}@Overridevoid push(E e){arraty.addLasy(e);}@OverrideE pop(){array.removeLast();}@OverrideE peek(){return array.getLast();}@Overridepublic String toString(){StringBuilder res = new StringBuilder();res.append("Stack: ");res.append("[]");for(int i  = 0 ; i < arr.getSize();i++){res.append(array.get(i));if(i!=array.getSize()-1)res.append(", ");}res.append("] top");return res.toString();}
}
对于array新加如下方法
public E getLast(){return get(size-1);
}
public E getFirst(){return get(0);
}

栈的另一个应用，括号匹配

这是二十家大公司对于该题的面试形式

栈顶元素反映了在嵌套的层次关系中，最近的需要匹配的元素

Class Solution{public boolean isValid(String s){Stack<Character> stack = new Stack<>();for(int i  = 0 ; i <s.length();i++)char c = s.charAt(i);if(c=='('||c=='['||c=='{')stack.push(c);else{if(stack.isEmpty())return false;char topChar = stack.pop();if(c==')'&&topChar!='(')return false;if(c==']'&&topChar!='[')return false;if(c=='}'&&topChar!='{')return false;}return stack.isEmpty();}
}

队列

队列也是一种线性结构
相比数组，队列对应的操作是数组的子集
只能从一端添加元素，从另一端取出元素
队列是一种先进先出的数据结构（先到先得）
First　Iｎ First Out(FIFO)

Queue<E>
- void enqueue(E)//入队
- E dequeue()//出队
- E getFront()//获取队首元素
- int getSize()
- boolean isEmpty()//是否为空

public interface Queue<E>{void enqueue(E)//入队E dequeue()//出队E getFront()//获取队首元素int getSize()boolean isEmpty()//是否为空
}
public class ArrayQueue<E> implements Queue<E>{private Array<E> array;public ArrayQueue(int capacity){array = new Array<>(capacity);}public ArrayQueue(){array = new Array<>();}@Overridepublic int getSize(){return array.getSize();}@Overridepublic int isEmpty(){return array.isEmpty();}@Overridepublic int getCapacity(){return array.getCapacity();}@Overridepublic int enqueue(){array.addLast(e);}@Overridepublic int dequeue(){return array.removeFirst();}@Overridepublic E getFront(){return array.getFirst();}@Overridepublic String toString(){StringBuilder res = new StringBuilder();res.append("Queue: ");res.append("front [");for(int i  = 0 ; i < arr.getSize();i++){res.append(array.get(i));if(i!=array.getSize()-1)res.append(", ");}res.append("] tail");return res.toString();}
}

循环队列

数组队列的问题

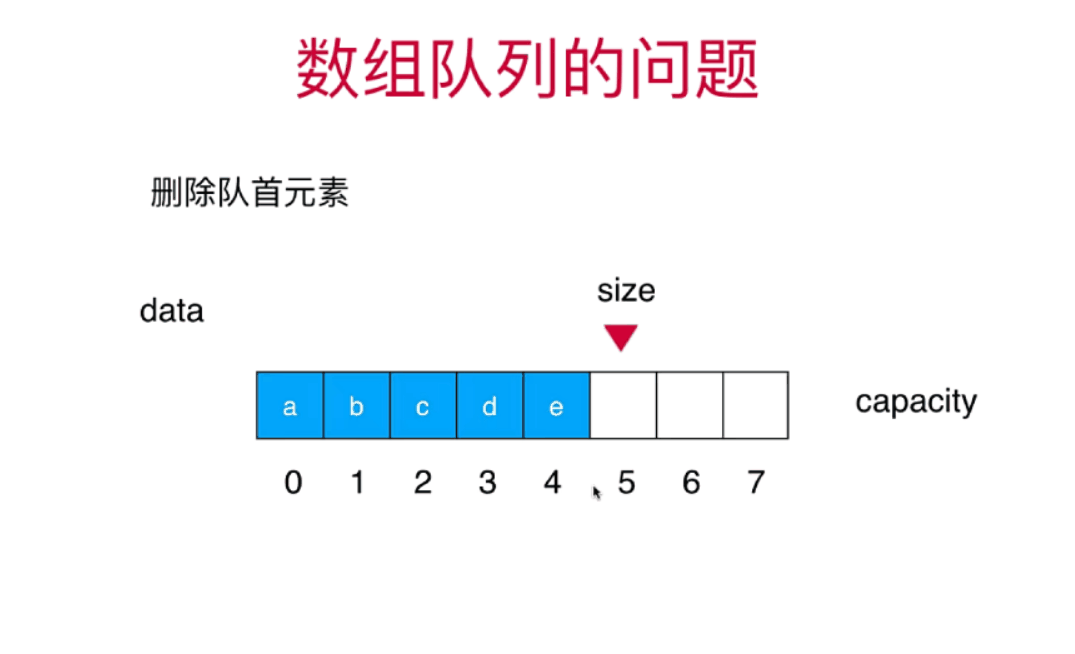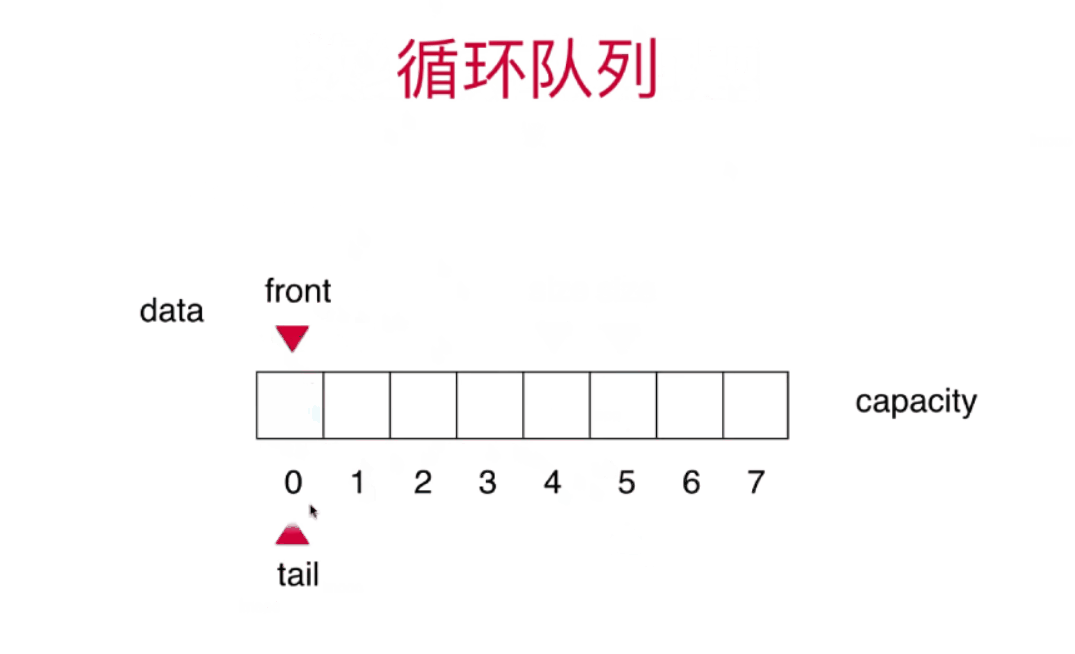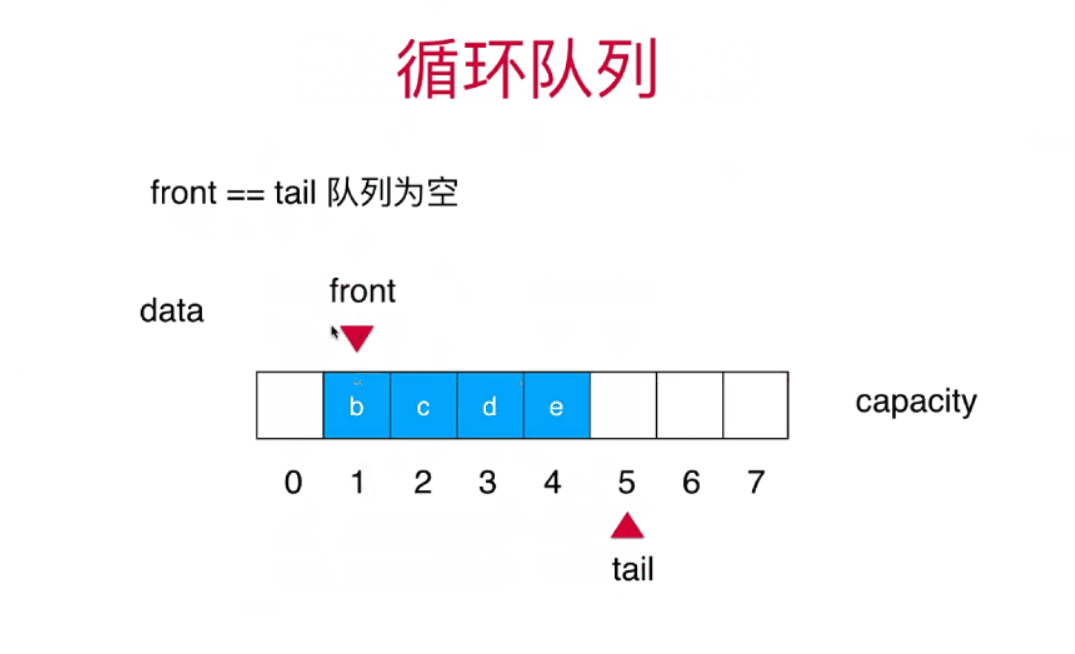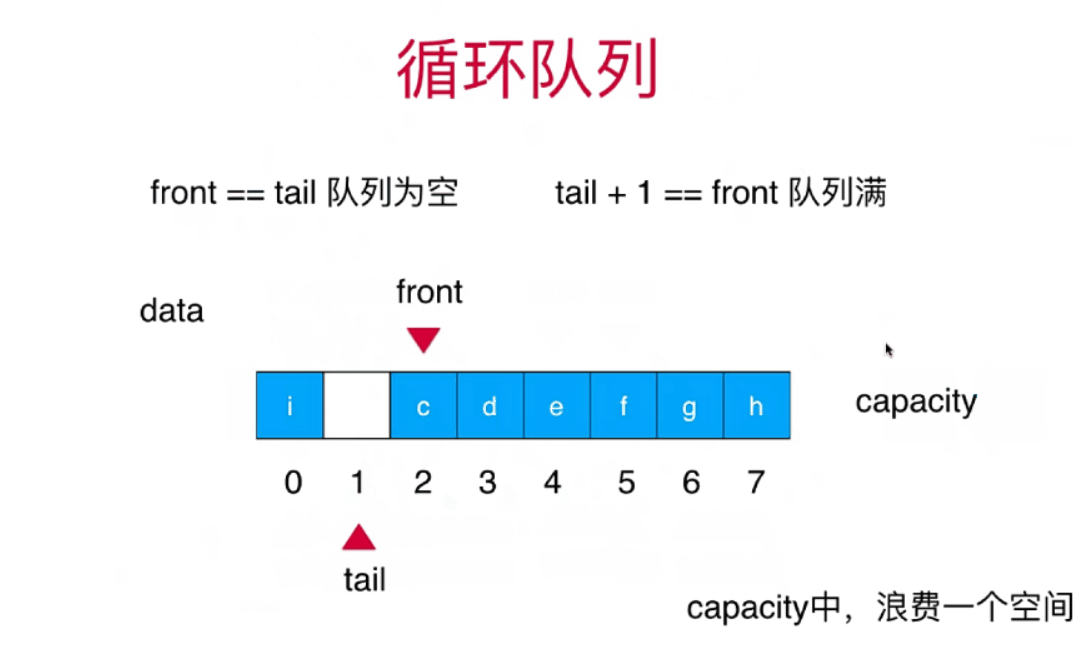
在这里插入图片描述

（tail+1)%c==front 队列满

对于循环我们可以查看自己的钟表就能理解了循环的意思。形成一个环，大小由数组容积决定。

public class LoopQueue<E> implements Queue<E>{private E[] data;private int front,tail;private int size;public LoopQueue(int capacity){data =(E[]) new Obejct[capacity+1];front = 0;tail  = 0;size = 0;}public LoopQueue(){this(10);}public int getCapacity(){return data.length-1;}@Overridepublic boolean isEmpty(){return front==tail;}@Overridepublic String toString(){StringBuilder res = new StringBuilder();res.append("Queue: size = %d, capacity = %d",size,getCapacity());res.append("front [");for(int i  = front ; i ! = tail;(i+1)%data.length){res.append(array.get(i));if((i+1)%data.length!=tail)res.append(", ");}res.append("] tail");return res.toString();}
}

循环队列的实现

	@Overridepublic void enqueue(E e){if((tail+1)%data.length==front)resize(getCpacity()*2);data[tail] = e;tail = (tail+1)%data.length;size++;}@Overridepublic E dequeue(){if(isEmpty())throw new IllegalArgumentException("cannot dequeue from an empty queue");E ret = data[front];data[front] = null;front = (front+1)%data.length;size--;if(size == getCapacity()/4&&resize(getCapacity()/2!=0)resize(getCapacity()/2);return ret;}private void resize(int newCapacity){E[] newData =(E[]) new Object[newCapacity+1];for(int i = 0; i < size ;i++){newData[i] = data[(i+front) % data.length];}data = newData;front = 0;tail = size;}@Overridepublic E getFront(){if(isEmpty())throw new IllegalArgumentException("from an empty queue");return data[front];}@Overridepublic String toString(){StringBuilder res = new StringBuilder();res.append("Queue: size = %d, capacity = %d",size,getCapacity());res.append("front [");for(int i  = front ; i ! = tail;(i+1)%data.length){res.append(array.get(i));if((i+1)%data.length!=tail)res.append(", ");}res.append("] tail");return res.toString();}