LeetCode 124 —— 二叉树中的最大路径和
阅读目录
- 1. 题目
- 2. 解题思路
- 3. 代码实现
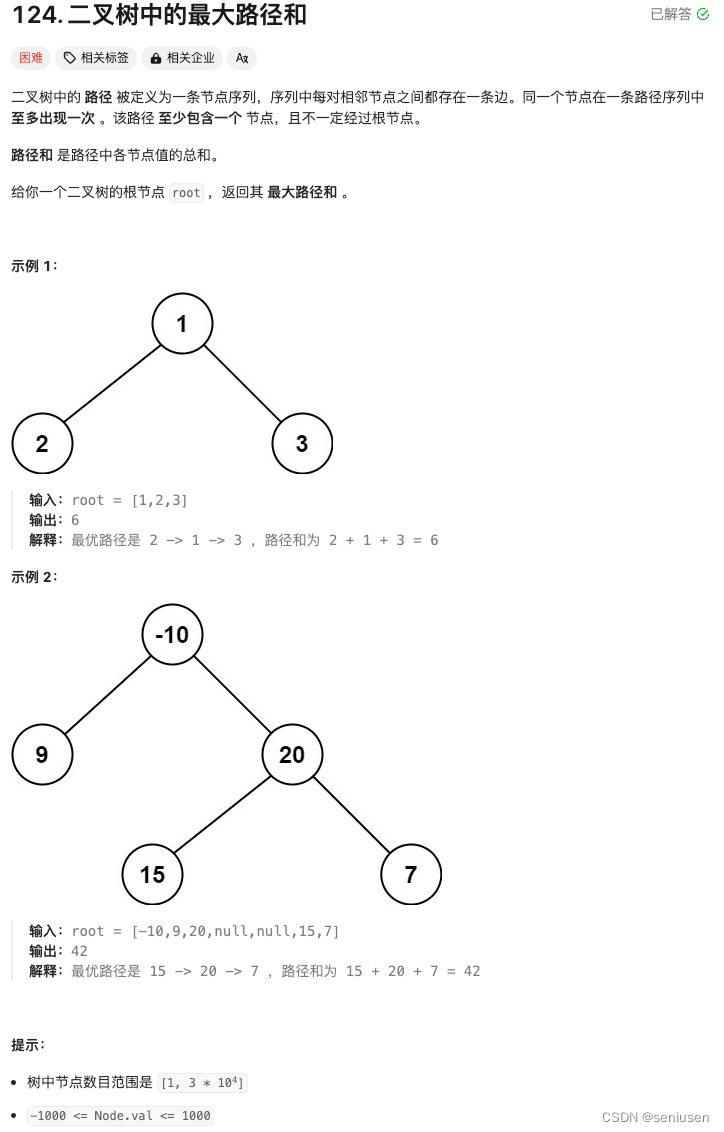
1. 题目
2. 解题思路
二叉树的问题首先我们要想想是否能用递归来解决,本题也不例外,而递归的关键是找到子问题。
我们首先来看看一棵最简单的树,也就是示例 1。这样的一棵树总共有六条路径,分别是:根节点、左节点-根节点、右节点-根节点、左节点、右节点、左节点-根节点-右节点,我们用一个大小为 6 的数组 rootSum 来分别表示这六条路径的路径和,那么所求的最大路径和即为 rootSum 的最大值。
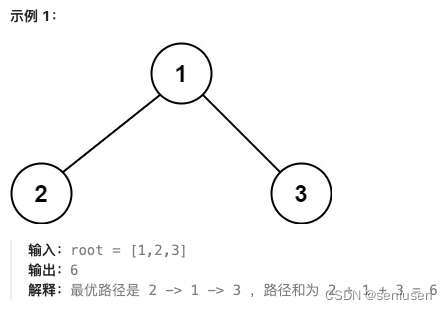
需要注意,当某一个节点为空的时候,比如左节点为空,那么左节点-根节点路径和为根节点的值,左节点贡献值为 0。而单独左节点的路径不存在,路径和应该设置为一个极大的负值。
接下来,我们再考虑一个更复杂的树,这棵树的根节点有左右两棵子树,每一棵子树都是类似上面示例 1 的一棵树。那么,我们可以很容易地得到左右子树的路径和数组 leftSum 和 rightSum ,接下来,我们要做的就是如何根据这两个数组得到整棵树的路径和数组 rootSum ?
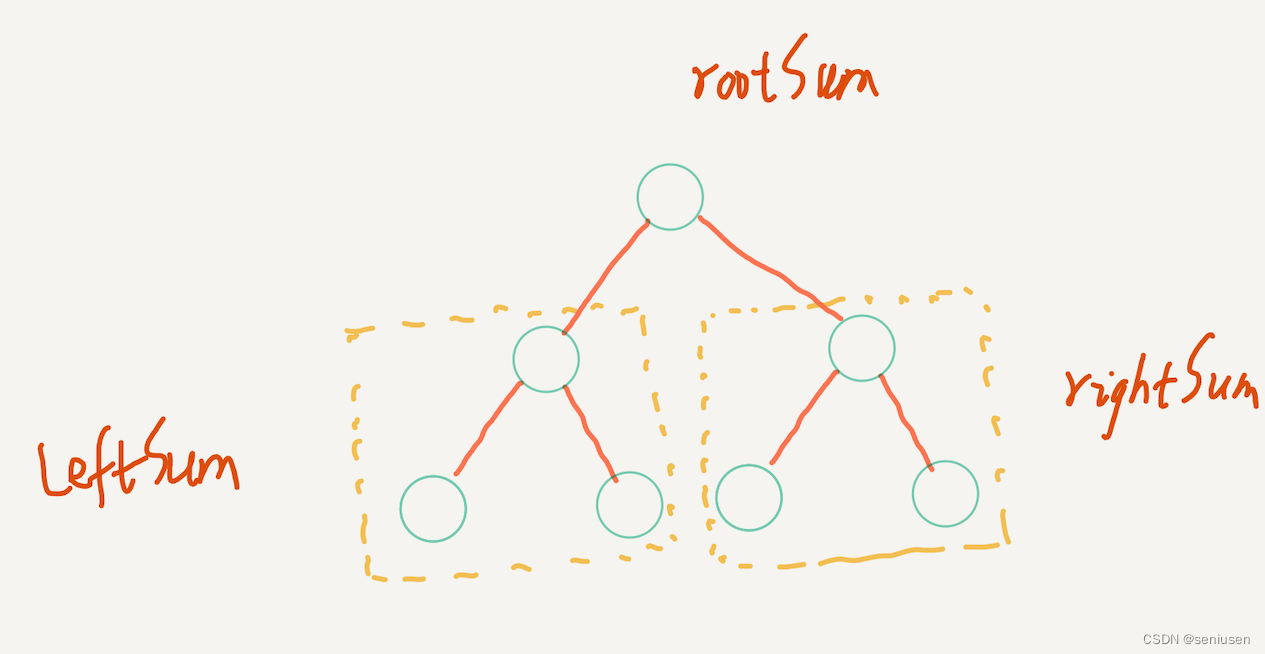
rootSum 仍然有 6 条路径,其中:
- 只有一个根节点的路径,
rootSum[0]=root->val - 左节点-根节点的路径,这时候由于左节点是一棵子树,所以,只有包含子树中根节点的路径才能继续和当前的根节点组成新的路径,也就是子树的前三条路径,然后我们取其中最大的一条即可,
rootSum[1]=root->val + max(leftSum[0:3)) - 右节点-根节点的路径,这个和上面的类似,
rootSum[2]=root->val + max(rightSum[0:3)) - 左节点,也即是单独左子树组成的最大路径,
rootSum[3]=max(leftSum[0:6)) - 右节点,也即是单独右子树组成的最大路径,
rootSum[4]=max(rightSum[0:6)) - 左节点-根节点-右节点,也就是左子树的路径包含左子树的根节点,右子树的路径包含右子树的根节点,
rootSum[5]=max(leftSum[0:3))+ root->val + max(rightSum[0:3))
时间复杂度为 O ( n ) O(n) O(n), n n n 代表节点总数,每个节点都需要进行遍历一次,空间复杂度为 O ( n ) O(n) O(n),每个节点都需要存储 6 个状态值。
3. 代码实现
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> getNodePathSum(TreeNode* root) {int leftRootSum = 0, leftMaxSum = -10000;if (root->left != nullptr) {vector<int> leftSum = getNodePathSum(root->left);leftRootSum = *std::max_element(leftSum.begin(), leftSum.begin() + 3);leftMaxSum = *std::max_element(leftSum.begin(), leftSum.end());}int rightRootSum = 0, rightMaxSum = -10000;if (root->right != nullptr) {vector<int> rightSum = getNodePathSum(root->right);rightRootSum = *std::max_element(rightSum.begin(), rightSum.begin() + 3);rightMaxSum = *std::max_element(rightSum.begin(), rightSum.end());}vector<int> rootSum(6, 0);rootSum[0] = root->val;rootSum[1] = leftRootSum + root->val;rootSum[2] = rightRootSum + root->val;rootSum[3] = leftMaxSum;rootSum[4] = rightMaxSum;rootSum[5] = leftRootSum + root->val + rightRootSum;return rootSum;}int maxPathSum(TreeNode* root) {vector<int> sum = getNodePathSum(root);return *std::max_element(sum.begin(), sum.end());}
};
