误差反向传播简介与实现
误差反向传播
- 导语
- 计算图
- 反向传播
- 链式法则
- 反向传播结构
- 加法节点
- 乘法节点
- 实现简单层
- 加法
- 乘法
- 激活函数层实现
- ReLU
- Sigmoid
- Affine/Softmax层实现
- Affine
- 基础版
- 批版本
- Softmax-with-Loss
- 误差反向传播实现
- 梯度确认
- 总结
- 参考文献
导语
书上在前一章介绍了随机梯度下降法进行参数与权重的学习,但是实际上,SGD的训练过程很慢,并且,神经网络层与层之间是存在数学关系的,SGD并没有利用好他们间的这种关系,相比之下,利用数学式关系的误差反向传播,无论是在效率还是速度上都相较于随机梯度下降更胜一筹,也更为常用。
计算图
书上采用了计算图来描述传播过程,这里的图和数据结构中的图定义一样,简单实例如下:

如图,一般来说,计算图时一个有向无环图,使用计算图时需要先构建,然后再从左往右计算,像从左到右的计算方向,称之为正向传播(从出发点到结束点,有点类似网络流)。
计算图可以通过传递局部计算的结果来一层层的获得最终结果,如图中的x×y,这是一个局部结果,并不会干扰别的传递,计算图就是通过一步一步,一个个局部运算,最后得到结果的。
反向传播
如图,反向传播的计算顺序与正向传播相反,将信号E乘以局部导数,然后将结果传递下一个节点,局部导数为y关于x的导数,因为存在多参数的情况,所以这里是偏导,这种偏导是基于链式法则来实现的。

链式法则
链式法则是关于复合函数导数的性质,定义为:如果某个函数由复合函数表示,则该复合函数的导数可以由构成函数的各个函数的导数乘积表示。
具体的例子和证明属于高等数学内容,略,这里只说明链式法则和计算图的内容,一个简单的示例图如下。

根据链式法则∂z/∂t · ∂t/∂x=∂z/∂x,而原式 z = ( x − y ) 2 z=(x-y)^2 z=(x−y)2,则∂z/∂x= 2 ( x − y ) 2(x-y) 2(x−y)
反向传播结构
一般来说,计算图涉及到的运算都可以用加法和乘法表示,减法可以变成加负数,除法可以变成乘倒数,因此书上主要介绍了反向传播的加法节点和乘法节点的结构。
加法节点
以 z = x + y z=x+y z=x+y为例,计算图表示如下:

z对x,y的偏导都为1,反向传播图如下:

书上把上游传来的导数值设为∂L/∂z(最终输出值),由于链式法则,反向传播向下传递时要乘以z对x,y的偏导。
乘法节点
以 z = x y z=xy z=xy为例,计算图表示如下:

z对x,y的偏导分别为y、x,反向传播图如下:

可以看到,加法的反向传播只是将上游值传给下游,是不需要输入信号的,但是乘法的反向传播是需要正向传播的输入信号的。
实现简单层
承接上文,实现计算图中的乘法节点的,就是乘法层,实现加法节点就是加法层。
加法
给出书上的代码,方便理解加上了注释,按照个人习惯修改了一下:
class MulLayer:def __init__(self):#初始化self.x = Noneself.y = Nonedef forward(self, x, y):#赋值和返回正向传播结果self.x=xself.y=y return x*ydef backward(self, dout):#返回反向传播结果,注意需要输入导数return dout*self.y,dout*self.x乘法
同上:
class AddLayer:def __init__(self):#不需初始化passdef forward(self, x, y):#正向传播return x+ydef backward(self, dout):#反向传播return dout*1,dout*1激活函数层实现
在书的上一章实现了神经网络的学习,但是只有学习过程是不够的,还需要激活函数,对得到的结果进行取舍,书上在本章进行了激活函数层的实现。
ReLU
ReLU函数的性质不再赘述,可以参考神经网络简介,这里只给出计算图:

这里给出书上的实现,加上了一些注释:
class Relu:def __init__(self):self.mask = Nonedef forward(self, x):self.mask = (x <= 0)#返回所有非正下标out = x.copy()#深复制out[self.mask] = 0#对应下标全部置0return outdef backward(self, dout):dout[self.mask] = 0#对应下标全部置0return dout
Sigmoid
这里跳过了sigmod内部各个节点的传递过程,将其视为一个整体,直接给出计算图:

书上的实现:
class Sigmoid:def __init__(self):self.out = Nonedef forward(self, x):out = sigmoid(x)#输出self.out = out#赋值return outdef backward(self, dout):return dout*(1.0-self.out)*self.out#反向传播的导数式子
Affine/Softmax层实现
上文所给的函数,操作对象都是单个的数值,然而在神经网络中,我们操作的总是矩阵,因此需要对应的运算层来实现运算。
Affine
Affine用来实现神经网络的正向传播中的矩阵乘积运算,式子表达为 Y = X W + B Y=XW+B Y=XW+B,这里的计算图采用书上的例子,即取各数据维度: X X X为 ( 2 , ) (2,) (2,)、 W W W为 ( 2 , 3 ) (2,3) (2,3)、 B B B为 ( 3 , ) (3,) (3,),基本计算图如下:

基础版
矩阵计算图的反向传播和前文的道理一样,书上给出了反向传播的推导结果:
( 1 ) ∂ L ∂ X = ∂ L ∂ Y W T ( 2 ) ∂ L ∂ W = X T ∂ L ∂ Y \begin{aligned} (1)\frac{∂L}{∂X}=\frac{∂L}{∂Y}W^{T} \\ \\ (2)\frac{∂L}{∂W}=X^{T}\frac{∂L}{∂Y} \end{aligned} (1)∂X∂L=∂Y∂LWT(2)∂W∂L=XT∂Y∂L
反向传播的计算图如下,数字为对应的式子, X X X应该和 ∂ L ∂ X \frac{∂L}{∂X} ∂X∂L形状相同, W W W应该和 ∂ L ∂ W \frac{∂L}{∂W} ∂W∂L形状相同。

批版本
现在考虑N个数据一起进行正向传播的情况,即批版本Affine层,相较于只处理单个数据,批版本多加了一维,式子如下:
( 3 ) ∂ L ∂ B = ∂ L ∂ Y \begin{aligned} (3)\frac{∂L}{∂B}=\frac{∂L}{∂Y} \end{aligned} (3)∂B∂L=∂Y∂L
计算图如下,可以看到都多加了一维,输入从一个数组变成了矩阵。

需要注意的是,就偏置值来说,正向传播和反向传播的处理方式是不一样的,正向传播只需要对每个数据加上相同的偏置值,但是反向传播,由于上有传回的数据不同,所以得到的偏导也可能不同,所以反向传播时得到的应该是一个数组。
书上给出的实现如下:
class Affine:def __init__(self, W, b):self.W =Wself.b = bself.x = Noneself.original_x_shape = None# 权重和偏置参数的导数self.dW = Noneself.db = Nonedef forward(self, x):# 对应张量self.original_x_shape = x.shapex = x.reshape(x.shape[0], -1)#重新拉伸self.x = xreturn np.dot(self.x, self.W) + self.bdef backward(self, dout):dx = np.dot(dout, self.W.T)self.dW = np.dot(self.x.T, dout)self.db = np.sum(dout, axis=0) return dx.reshape(*self.original_x_shape)# 还原输入数据的形状(对应张量)
Softmax-with-Loss
书上给出的softmax层的实现包括了损失函数,因此叫Softmax-with-Loss,由于太过复杂没办法重绘,这里给出书上设计图:

简化版的如下,这里假设要进行三类分类。
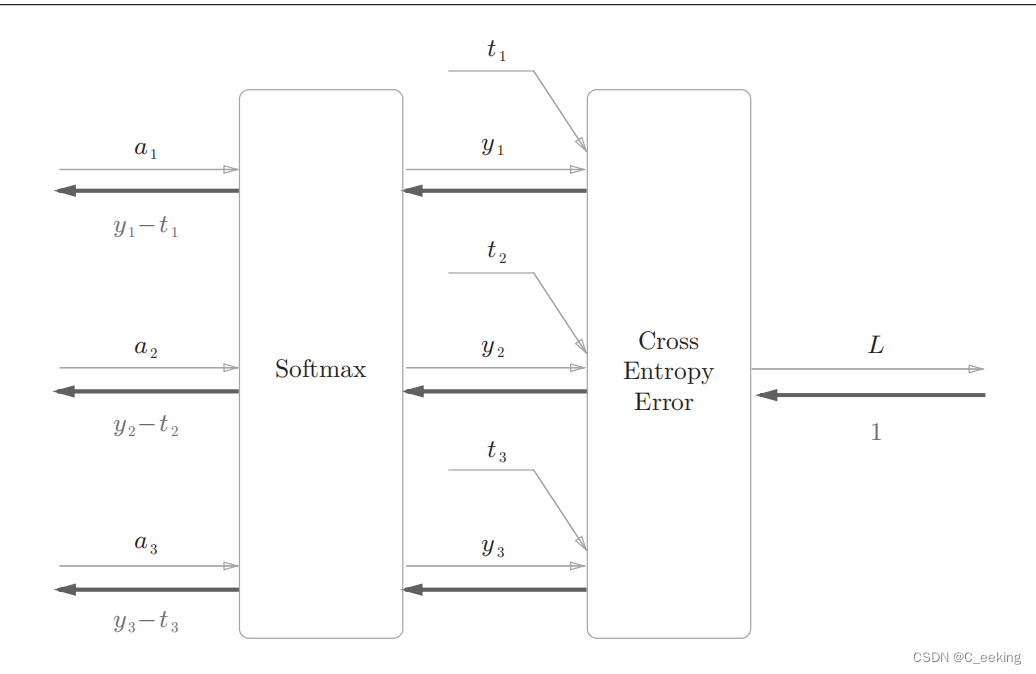 书上给出的代码实现如下:
书上给出的代码实现如下:
class SoftmaxWithLoss:def __init__(self):self.loss = Noneself.y = None # softmax的输出self.t = None # 监督数据def forward(self, x, t):self.t = tself.y = softmax(x)self.loss = cross_entropy_error(self.y, self.t)return self.lossdef backward(self, dout=1):#反向传播时要除以批大小,传递前面的层是单个数据的误差batch_size = self.t.shape[0]if self.t.size == self.y.size: # 监督数据是one-hot-vector的情况dx = (self.y - self.t) / batch_sizeelse:dx = self.y.copy()dx[np.arange(batch_size), self.t] -= 1dx = dx / batch_sizereturn dx
误差反向传播实现
上一章的神经网络实现使用数值微分求得,在使用时效率很低,如果使用误差反向传播效率会更高,这里给出书上的两层网络实现,加上了一些注释:
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDictclass TwoLayerNet:def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):#输入规模,隐藏层规模,输出规模,分布参数# 初始化权重self.params = {}self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)#高斯本部self.params['b1'] = np.zeros(hidden_size)#全置0self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size) self.params['b2'] = np.zeros(output_size)# 生成层self.layers = OrderedDict()#有序字典,记住向字典添加的顺序,可以认为拿字符串作为每一层的下标了self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])#传入参数,生成层self.layers['Relu1'] = Relu()self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])self.lastLayer = SoftmaxWithLoss()#最后一层def predict(self, x):#递推,每一层的结果作为下一层输入for layer in self.layers.values():x = layer.forward(x)return x# x:输入数据, t:监督数据def loss(self, x, t):y = self.predict(x)return self.lastLayer.forward(y, t)def accuracy(self, x, t):y = self.predict(x)y = np.argmax(y, axis=1)if t.ndim != 1 : t = np.argmax(t, axis=1)accuracy = np.sum(y == t) / float(x.shape[0])return accuracy# x:输入数据, t:监督数据def numerical_gradient(self, x, t):#反向传播算梯度loss_W = lambda W: self.loss(x, t)grads = {}grads['W1'] = numerical_gradient(loss_W, self.params['W1'])grads['b1'] = numerical_gradient(loss_W, self.params['b1'])grads['W2'] = numerical_gradient(loss_W, self.params['W2'])grads['b2'] = numerical_gradient(loss_W, self.params['b2'])return gradsdef gradient(self, x, t):# forwardself.loss(x, t)# backwarddout = 1dout = self.lastLayer.backward(dout)layers = list(self.layers.values())layers.reverse()for layer in layers:#一层层往回推dout = layer.backward(dout)# 设定grads = {}grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].dbgrads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].dbreturn grads
训练的源码略,只需要进行下列修改即可。
 学习的结果如下,输出的是训练集和测试集上的准确度:
学习的结果如下,输出的是训练集和测试集上的准确度:

梯度确认
与反向传播相比,数值微分的效率显得捉襟见肘,这是否意味着数值微分没有用武之地了呢?并不是,由于误差反向传播实现很复杂,所以很容易出错,因此,在用误差传播得到结果后,可以用数值微分的结果进行比对,确认误差传播的实现是否正确,这样的过程就是梯度确认,书上给的代码如下:
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)#拿数据network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)#构造神经网络x_batch = x_train[:3]
t_batch = t_train[:3]grad_numerical = network.numerical_gradient(x_batch, t_batch)#数值微分
grad_backprop = network.gradient(x_batch, t_batch)#反向传播for key in grad_numerical.keys():diff = np.average( np.abs(grad_backprop[key] - grad_numerical[key]) )#秋各个权重的绝对误差平均值print(key + ":" + str(diff))
运行结果:

总结
相较于数值微分,误差反向传播是一个更好的实现方式,但是理解上和实现上也增加了困难,并且由于其自身的复杂性,往往还需要数值微分进行结果的比对。
参考文献
- 《深度学习入门——基于Python的理论与实现》
