当前位置：首页 > news >正文

SQL如何利用Bitmap思想优化array_contains()函数

news 2025/8/9 19:14:09

0 问题描述

1 位图思想

2 案例实战

3 小结

0 问题描述

在工作中，我们往往使用array_contains()函数来进行存在性问题分析，如判断某个数是否在某个数组中，但是当表数据量过多，存在大量array_contains()函数时，就会存在一定性能问题，为了优化该函数的性能，本文主要利用位图的方法来代替array_contains()函数。

1 位图思想

在本文之前读者需要先了解位图的概念及位图的一些性质，本文关于位图的概念不再重复。假如我们有如下需求，如下图所示，我们想判读数字2,5,7是否在数组[1,2,3,5,6]中时，如果用位图我们应该怎么做？通过两个位图相与就可以求出交集，通过下图可以看出bitmap1&bitmap2，可以求出交集2和5在数组中，因此关于此性质，我们可以得到判读存在性问题时，我们只需要构建两个位图与，结果有值不为0则为存在，那么问题来了，如何通过SQL的形式去构建呢？

相比大家对8421码比较熟悉，如1111，如下图所示

上述的式子我们可以进行如下等价

1111=15=1*2^0 + 1 * 2^1 + 1 * 2^2 + 1 * 2^3 <=> 1 << 0 + 1 << 1 + 1 << 2 + 1 << 3

因此我们构建数组 [1,2,3,5,6] 在位图中反应即为：

存在记为1，不存在记为0，即序列 01101110

那我们如何用SQL语言反应上述表达式呢？根据前面的等价转换，我们知道要反应01101110序列

即为：01101110=1*2^1 + 1*2^2 + 1*2^3 + 1*2^5 + 1*2^6 = 1 << 1 + 1 << 2 + 1 << 3 + 1 << 5 + 1 << 6。因此只要我们数据库中支持位移运算，就可以等价上述表达式。那么我们怎么判断数字2是否在上述数组中呢?数字2的位图根据以上推导，我们可以很快得出 1 << 2,而是否存在，只需要两者之间进行与运算即可，即：(1 << 2) &( 1 << 1 + 1 << 2 + 1 << 3 + 1 << 5 + 1 << 6),计算过程如下：

01101110
& 00000010
————————————————
00000010 =2

总结上述规律，我们得出如下判断公式：

假设判断某个num是否在数组[a,b,c,d]中时，可用如下公式：
if{

(1 << num) & (1 << a + 1 << b + 1 << c + 1 << d) = num
then true
else false

};

上述操作对应不同数据库操作符不一样，如何hive中使用shiftleft函数，doris中采用bit_shift_ left()函数，greenplum中直接为 <<操作符。

2 案例实战

如下2张表tbl1,tbl2，假设表数据量很大，判断tbl2中的col1字段是否在表tbl1中对应的id num字段中。

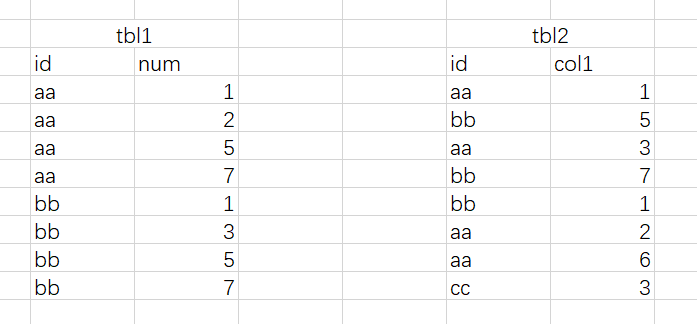
具体SQL如下：

select  t1.id, col1,case when (1 << col1) & num ) = col1 then true else false end true_or_false_flgfrom tbl1 t1
left join
(select id ,sum(1 << num) numfrom tbl2group by id ) t2
on t1.id = t2.id

读者在遇到相关问题时，可以根据自己具体的场景进行等价变换，这里只是抛砖引玉说明具体使用方法、