重温数据结构与算法之深度优先搜索
文章目录
- 前言
- 一、实现
- 1.1 递归实现
- 1.2 栈实现
- 1.3 两者区别
- 二、LeetCode 实战
- 2.1 二叉树的前序遍历
- 2.2 岛屿数量
- 2.3 统计封闭岛屿的数目
- 2.4 从先序遍历还原二叉树
- 参考
前言
深度优先搜索(Depth First Search,DFS)是一种遍历或搜索树或图数据结构的算法。该算法从根节点开始(在图的情况下,选择一些任意的节点作为根节点),并在回溯之前尽可能地沿着每个分支进行探索。需要额外的内存,通常是一个堆栈,来跟踪到目前为止沿着指定分支发现的节点,这有助于回溯。
深度优先搜索算法的特点:
- 从一个起始节点开始,沿着一条路径不断访问邻接节点,直到没有未访问的邻接节点为止,然后回溯到上一个节点,继续访问其他邻接节点。
- 利用栈或递归来实现。
- 可以产生目标图的相应拓扑排序表。
深度优先搜索算法的优点:
- 简单易实现。
- 占用空间少。
- 可以找到从起始节点到任意可达节点的路径。
深度优先搜索算法的缺点:
- 不一定能找到最短路径或最优解。
- 可能会陷入死循环或无限递归。
深度优先搜索算法的应用场景:
- 拓扑排序 (课程安排、工程进度、依赖关系)
- 模拟游戏(如象棋、迷宫等)
- 连通性检测(如判断图中是否有环等)
- 旅行商问题(如求解最短路径等)
- 括号匹配(如检查表达式中的括号是否匹配等)
- 二叉树、线段树、红黑树、图等数据结构的遍历
在本文中,我们将介绍深度优先搜索算法的基本原理和实现方法,并通过一些例题来展示其应用。
一、实现
1.1 递归实现
从一个起始节点开始,沿着一条路径不断访问邻接节点,直到没有未访问的邻接节点为止,然后回溯到上一个节点,继续访问其他邻接节点,直到所有节点都被访问过为止。
示例代码如下:
public void dfs(int start) {visited[start] = true; //将起始节点标记为已访问for (int i = 0; i < n; i++) { //遍历邻接矩阵中start所在行if (matrix[start][i] == 1 && !visited[i]) { //如果存在边且未被访问过dfs(i); //递归调用dfs方法,以该节点为新起点进行遍历}}
}
1.2 栈实现
从一个起始节点开始,将其压入栈中,然后重复以下步骤:弹出栈顶元素,并将其标记为已访问;将该元素的所有未访问的邻接节点压入栈中。直到栈为空为止
示例代码如下:
public void dfs(int start) {Stack<Integer> stack = new Stack<>(); //创建栈对象stack.push(start); //起始节点入栈Set<Integer> visited = new HashSet<>(); //创建集合对象visited.add(start); //起始节点加入集合while (!stack.isEmpty()) { //只要栈不为空就继续循环int cur = stack.peek(); //获取栈顶元素但不出栈boolean flag = false; //设置标志位,表示是否有未访问过的邻接节点for (int i = 0; i < n; i++) { //遍历邻接矩阵中cur所在行if (matrix[cur][i] == 1 && !visited.contains(i)) { //如果存在边且未被访问过stack.push(i); //将该节点入栈visited.add(i); //将该节点加入集合System.out.print(i + " "); //打印该节点flag = true; //修改标志位为true,表示有未访问过的邻接节点break; //跳出循环,以该节点为新起点进行遍历}}if (!flag) { //如果没有未访问过的邻接节点,则说明已经到达最深处,需要回溯上一层继续遍历其他分支路径。stack.pop(); //将栈顶元素出栈 }}
}
下面是一个dfs搜索的动图
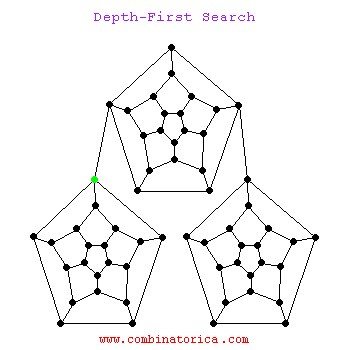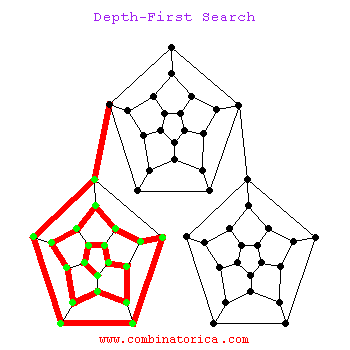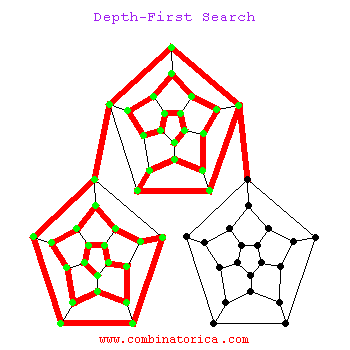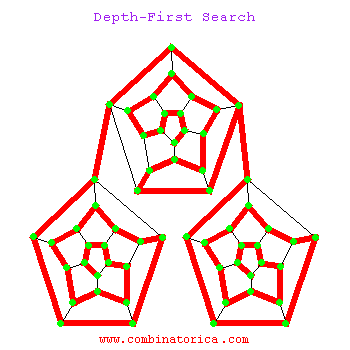
1.3 两者区别
- 递归实现是利用系统栈来保存当前节点的状态,当遇到死路时,自动回溯到上一个节点继续搜索。而栈实现是利用自定义的栈来保存当前节点的状态,当遇到死路时,手动弹出栈顶元素回溯到上一个节点继续搜索。
- 递归实现比较简洁易懂,但是效率不高,而且对于规模较大的图可能会导致栈溢出。而栈实现比较复杂一些,但是效率更高,而且可以避免栈溢出的问题。
- 递归实现和栈实现都需要一个标志数组来记录哪些节点已经被访问过,以防止重复访问或者陷入环路。
二、LeetCode 实战
2.1 二叉树的前序遍历
94. 二叉树的前序遍历
给你二叉树的根节点
root,返回它节点值的 前序 遍历。
List<Integer> ans = new ArrayList(); //定义一个整数列表,用来存储前序遍历的结果
public List<Integer> preorderTraversal(TreeNode root) {if (root != null) { //如果当前节点不为空,才进行以下操作ans.add(root.val); //把当前节点的值加入列表preorderTraversal(root.left); //递归地对左子树进行前序遍历preorderTraversal(root.right); //递归地对右子树进行前序遍历}return ans; //返回前序遍历的结果
}
2.2 岛屿数量
200. 岛屿数量
给你一个由
'1'(陆地)和'0'(水)组成的的二维网格,请你计算网格中岛屿的数量。岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
// 定义一个二维数组pos,表示四个方向
int[][] pos = { { 0, 1 }, { 1, 0 }, { 0, -1 }, { -1, 0 } };
// 定义一个变量ans,表示岛屿的数量
int ans = 0;// 定义一个方法numIslands,接受一个二维字符数组grid作为参数,返回岛屿的数量
public int numIslands(char[][] grid) {// 获取grid的行数和列数int m = grid.length, n = grid[0].length;// 定义一个二维布尔数组visited,表示每个位置是否被访问过boolean[][] visited = new boolean[m][n];// 遍历grid中的每个位置for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {// 如果当前位置是'1'且没有被访问过,则从该位置开始深度优先搜索,并将ans加一if (grid[i][j] == '1' && !visited[i][j]) {dfs(grid, visited, i, j);ans++;}}}// 返回ans作为结果return ans;
}// 定义一个方法dfs,接受一个二维字符数组grid、一个二维布尔数组visited、两个整数i和j作为参数,无返回值
public void dfs(char[][] grid, boolean[][] visited, int i, int j) {// 如果i或j越界或者当前位置是'0'或者已经被访问过,则直接返回if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] == '0'|| visited[i][j]) {return;}// 将当前位置标记为已访问visited[i][j] = true;// 遍历四个方向,并递归调用dfs方法for (int[] p : pos) {dfs(grid, visited, i + p[0], j + p[1]);}}
2.3 统计封闭岛屿的数目
1254. 统计封闭岛屿的数目
二维矩阵
grid由0(土地)和1(水)组成。岛是由最大的4个方向连通的0组成的群,封闭岛是一个完全由1包围(左、上、右、下)的岛。请返回 封闭岛屿 的数目。
// 定义一个二维数组pos来存储上下左右四个方向的偏移量
int[][] pos = { { 0, 1 }, { 1, 0 }, { 0, -1 }, { -1, 0 } };
// 定义一个变量ans来记录封闭岛屿的个数
int ans = 0;public int closedIsland(int[][] grid) {// 判断矩阵是否为空,如果为空,直接返回0if (grid == null || grid.length == 0 || grid[0].length == 0) {return 0;}// 获取矩阵的行数和列数int m = grid.length, n = grid[0].length;// 遍历矩阵中的每一个元素for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {// 如果当前元素是岛屿(0),则调用dfs函数来检查它是否被水域(1)完全包围if (grid[i][j] == 0 && dfs(grid, i, j)) {// 如果dfs函数返回true,说明当前岛屿是封闭的,ans加一ans++;}}}// 返回ans作为最终答案return ans;
}
public boolean dfs(int [][] grid, int i, int j) {// 如果当前坐标超出了矩阵的边界,说明当前岛屿不是封闭的,返回falseif (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length) {return false;}// 如果当前元素是水域(1),说明没有遇到边界,返回trueif (grid[i][j] == 1) {return true;}// 将当前元素标记为水域(1),避免重复访问grid[i][j] = 1;// 使用一个for循环来遍历上下左右四个方向,并将结果进行逻辑与运算boolean res = true;for (int [] p: pos) {res &= dfs(grid, i + p[0], j + p[1]);}// 返回res作为dfs函数的结果return res;
}
2.4 从先序遍历还原二叉树
1028. 从先序遍历还原二叉树
我们从二叉树的根节点
root开始进行深度优先搜索。在遍历中的每个节点处,我们输出
D条短划线(其中D是该节点的深度),然后输出该节点的值。(如果节点的深度为D,则其直接子节点的深度为D + 1。根节点的深度为0)。如果节点只有一个子节点,那么保证该子节点为左子节点。
给出遍历输出
S,还原树并返回其根节点root。
int index = 0; // 定义全局变量indexpublic TreeNode recoverFromPreorder(String traversal) {int[] deep = Arrays.stream(traversal.split("[0-9]{1,10}")).mapToInt(String::length).toArray(); // 将输入字符串按照数字分割成数组deepint[] number = Arrays.stream(traversal.split("-{1,100}")).mapToInt(Integer::parseInt).toArray(); // 将输入字符串按照连字符分割成数组numberif (deep.length == 0) deep = new int[]{0}; // 如果deep为空,则赋值为[0]return dfs(deep, number); // 调用dfs函数并返回结果
}public TreeNode dfs(int [] deep, int [] number) {TreeNode treeNode = new TreeNode(number[index]); // 创建新的TreeNode对象并赋值int curHeight = deep[index]; // 获取当前节点的深度if (index + 1 < deep.length && curHeight == deep[index + 1] - 1) { // 判断是否有左子节点index++; // 将index加1treeNode.left = dfs(deep, number); // 递归调用dfs并赋值给左子节点}if (index + 1 < deep.length && curHeight == deep[index + 1] - 1) { // 判断是否有右子节点index++; // 将index加1treeNode.right = dfs(deep, number); // 递归调用dfs并赋值给右子节点}return treeNode; // 返回当前节点
}
参考
- https://en.wikipedia.org/wiki/Depth-first_search
- https://zh.wikipedia.org/wiki/深度优先搜索
- 深度优先搜索 —— 新手上路的一道坎
