统计学习--三种常见的相关系数
1)Pearson积差相关系数:用于量度两个变量X和Y之间的线性相关。它具有+1和-1之间的值,其中1是总正线性相关性,0是非线性相关性,并且-1是总负线性相关性。Pearson相关系数的一个关键数学特性是它在两个变量的位置和尺度的单独变化下是不变的。也就是说,我们可以将X变换为a+bX并将Y变换为c+dY,而不改变相关系数,其中a,b,c和d是常数,b,d > 0。请注意,更一般的线性变换确实会改变相关性。
Pearson积差相关系数对应的计算公式如下:
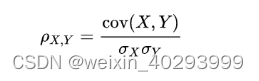
积差相关系数的适用条件: 在相关分析中首先要考虑的问题就是两个变量是否可能存在相关关系,如果得到了肯定的结论,那才有必要进行下一步定量的分析。另外还必须注意以下几个问题:
1、 积差相关系数适用于线性相关的情形,对于曲线相关等更为复杂的情形,积差相关系数的大小并不能代表相关性的强弱。
2、 样本中存在的极端值对Pearson积差相关系数的影响极大,因此要慎重考虑和处理,必要时可以对其进行剔出,或者加以变量变换,以避免因为一两个数值导致出现错误的结论。 3、 Pearson积差相关系数要求相应的变量呈双变量正态分布,注意双变量正态分布并非简单的要求x变量和y变量各自服从正态分布,而是要求服从一个联合的双变量正态分布。 以上几条要求中,前两者的要求最严,第三条比较宽松,违反时系数的结果也是比较稳健的。
2)Spearman秩相关系数:使利用两变量的秩次大小作线性相关分析,对原始变量的分布不做要求,属于非参数统计方法。因此它的适用范围比Pearson相关系数要广的多。即使原始数据是等级资料也可以计算Spearman相关系数。对于服从Pearson相关系数的数据也可以计算Spearman相关系数,但统计效能比Pearson相关系数要低一些(不容易检测出两者事实上存在的相关关系)。如果数据中没有重复值, 并且当两个变量完全单调相关时,斯皮尔曼相关系数则为+1或−1。Spearman相关系数即使出现异常值,由于异常值的秩次通常不会有明显的变化(比如过大或者过小,那要么排第一,要么排最后),所以对Spearman相关性系数的影响也非常小。
计算公式:对于样本容量为n的样本,n个原始数据被转换成等级数据,相关系数ρ为
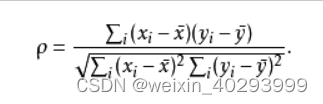
实际应用中,变量间的连结是无关紧要的,于是可以通过简单的步骤计算ρ.被观测的两个变量的等级的差值,则ρ为
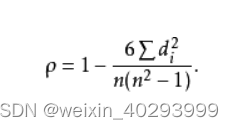
3)Kendall秩相关系数: 是一种秩相关系数,用于反映分类变量相关性的指标,适用于两个变量均为有序分类的情况,用希腊字母τ(tau)表示其值。
【分类变量可以理解成有类别的变量,可以分为无序的,比如性别(男、女)、血型(A、B、O、AB);有序的,比如肥胖等级(重度肥胖,中度肥胖、轻度肥胖、不肥胖)。通常需要求相关性系数的都是有序分类变量】
Kendall相关系数的取值范围在-1到1之间,当τ为1时,表示两个随机变量拥有一致的等级相关性;当τ为-1时,表示两个随机变量拥有完全相反的等级相关性;当τ为0时,表示两个随机变量是相互独立的。
计算公式:Kendall系数是基于协同的思想。对于X,Y的两对观察值Xi,Yi和Xj,Yj,如果Xi<Yi并且Xj<Yj,或者Xi>Yi并且Xj>Yj,则称这两对观察值是和谐的,否则就是不和谐。kendall相关系数的计算公式如下:

和谐的观察值对减去不和谐的观察值对的数量,除以总的观察值对数.
注意:三种相关系数都是对变量之间相关程度的度量,由于其计算方法不一样,用途和特点也不一样。
1)Pearson相关系数是在原始数据的方差和协方差基础上计算得到,所以对离群值比较敏感,它度量的是线性相关。因此,即使pearson相关系数为0,也只能说明变量之间不存在线性相关,但仍有可能存在曲线相关。
2)Spearman相关系数和kendall相关系数都是建立在秩和观测值的相对大小的基础上得到,是一种更为一般性的非参数方法,对离群值的敏感度较低,因而也更具有耐受性,度量的主要是变量之间的联系。
补充:无序分类变量的统计推断:卡方检验
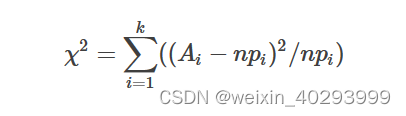
Ai为i水平的观测频数,Ei为i水平的期望频数,n为总频数,Pi为i水平的期望概率。 主要用于检验某无序分类变量各水平在两组或多组间的分布是否一致。还可以用于检验一个分类变量各水平出现的概率是否等于指定概率;一个连续变量的分布是否符合某种理论分布等。其主要用途:
1、 检验某个连续变量的分布是否与某种理论分布相一致。
2、 检验某个分类变量各类的出现概率是否等于制定概率。
3、 检验某两个分类变量是否相互独立。
4、 检验控制某种或某几种分类因素的作用以后,另两个分类变量是否相互独立。
5、 检验某两种方法的结果是否一致。
