【蓝桥杯】矩阵快速幂
一.快速幂概述
1.引例
1)题目描述:
求A^B的最后三位数表示的整数,A^B表示:A的B次方。
2)思路:
一般的思路是:求出A的B次幂,再取结果的最后三位数。但是由于计算机能够表示的数字的范围是有限的,所以会产生“指数爆炸”的现象(即发生溢出现象)。
换一种思路来看本题:
取模运算的公式如下:
结论:
多个因子连续的乘积取模的结果等于每个因子取模后的乘积再取模的结果。
我们可以借助这个法则,只需要在循环乘积的每一步都提前进行“取模”运算,而不是等到最后直接对结果“取模”,也能达到同样的效果。
3)代码如下:
long long normalPower(long long a,long long b){long long result=1;for(int i=0;i<b;i++){result=(result*(a%1000))%1000;}return result%1000;
}
2.快速幂算法
1)思路:
快速幂算法能够帮我们算出指数非常大的幂。
传统算法时间复杂度高的原因是:指数很大,循环次数多。
核心思想:每一步都将指数分成两半,而相应的底数做平方运算。
2)代码:
//获取最后三位数
long long fastPower(long long base,long long power){long long re=1;while(power>0){if(power%2){//指数为奇数power--;//指数-1,将其变为偶数re=re*base%1000;}power/=2;base=base*base%1000;}return re;
}通过位运算进行优化:
long long FastPower(long long base,long long power){long long re=1;while(power>0){if(power&1){re=re*base%1000;}power=power>>1;base=(base*base)%1000;}return re;
}二.矩阵快速幂
矩阵乘法:
for(i=1;i<=n;i++)
{for(j=1;j<=n;j++){for(k=1;k<=n;k++){c[i][j] += a[i][k] * b[k][j];}}
}矩阵快速幂:
仿照大数的快速幂
//矩阵快速幂
#include<iostream>
#include<cstring>
using namespace std;int M,n;struct node{int m[100][100];
}ans,res;//ans是结果,res为最初的方阵struct node mul(struct node A,struct node B){struct node C;int i,j,k;for(i=0;i<n;i++)for(j=0;j<n;j++)C.m[i][j]=0;for(i=0;i<n;i++){for(j=0;j<n;j++){for(k=0;k<n;k++){C.m[i][j]+=A.m[i][k]*B.m[k][j];}}}return C;
}void quickpower(){int i,j;//初始ans为单位矩阵for(i=0;i<n;i++)for(j=0;j<n;j++)if(i==j)ans.m[i][j]=1;elseans.m[i][j]=0;while(M>0){if(M&1){ans=mul(ans,res);}res=mul(res,res);M=M>>1;}
}
int main(){cin>>n;cin>>M;for(int i=0;i<n;i++)for(int j=0;j<n;j++)cin>>res.m[i][j];quickpower();for(int i=0;i<n;i++){for(int j=0;j<n;j++)cout<<ans.m[i][j]<<' ';cout<<endl;}return 0;
}
三.实战演练
1.题目描述:

2.问题分析:
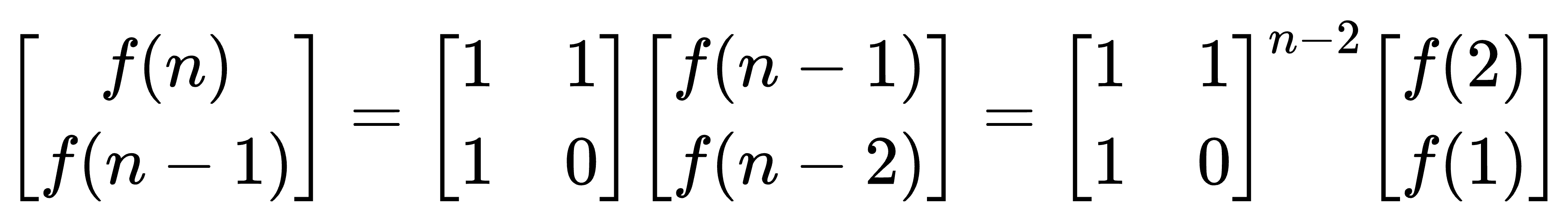
转换为矩阵相乘的形式。
3.代码实现:
//斐波那契数列
#include<iostream>using namespace std;const int N=1e4;
const long long mod=1e9+7;
int T;
long long a[N];struct node{long long m[2][2];
}ans,res;//矩阵乘法
struct node mul(struct node a,struct node b){struct node c;c.m[0][0]=(a.m[0][0]*b.m[0][0]+a.m[0][1]*b.m[1][0])%mod;c.m[0][1]=(a.m[0][0]*b.m[0][1]+a.m[0][1]*b.m[1][1])%mod;c.m[1][0]=(a.m[1][0]*b.m[0][0]+a.m[1][1]*b.m[1][0])%mod;c.m[1][1]=(a.m[1][0]*b.m[0][1]+a.m[1][1]*b.m[1][1])%mod;return c;
}//矩阵快速幂
struct node matrixPower(struct node base,long long exp){struct node res={1,0,0,1};while(exp>0){if(exp&1){res=mul(res, base);}exp=exp>>1;base=mul(base, base);}return res;
}//求斐波那契数列第n项
long long f(long long n){struct node base={1,1,1,0};struct node res=matrixPower(base, n-1);return res.m[0][0];
}
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>T;for(int i=0;i<T;i++){cin>>a[i];}for(int i=0;i<T;i++){cout<<f(a[i])<<'\n';}return 0;
}
