线性规划的标准型转换
对于任意给定的线性规划的问题,其实其本身可能是不符合线性规划标准型的需求的,但是如果通过一系列的等价变化的话,是可以将该问题转换为标准型的线性规划问题,例如如下的线性规划问题:
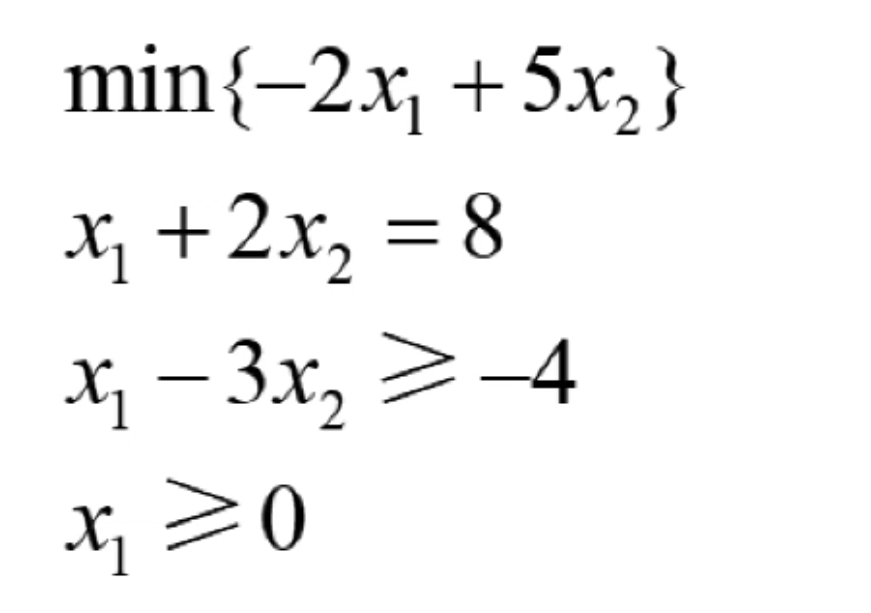
添加图片注释,不超过 140 字(可选)
给定的线性规划问题存在若干方面不满足最小值,首先就是目标函数是求最小值而不是求最大值,其次就是约束条件中的第2个不等式是大于等于而不是小于等于,最后就是这个问题只要求x1>=0,根据标准型的需求还必须有x2>=0,可以通过一系列的变化将其转换为标准型。
首先目标函数是求最小值,可以添加一个符号在目标函数前面转换成为求最大值,同时第二个约束条件是大于等于,因此在不等式的两边添加一个符号就会变成了小于等于,最后就是还需要再转换一个约束条件,那就是让所有变量都大于等于0,目前在约束条件只有x1>=0,但是对于x2是没有相应的约束的。
要想解决这个问题,常用思路就是对于没有大于等于0约束的变量xj,用两个变量来替换,也就是添加xj>=0,xj``>=0,使得xj=xj`-xj``,如此替换之后需要将约束条件中任何出现变量xj的地方替换成等号右侧的式子,于是原来的线性规划系统调整后转换为:
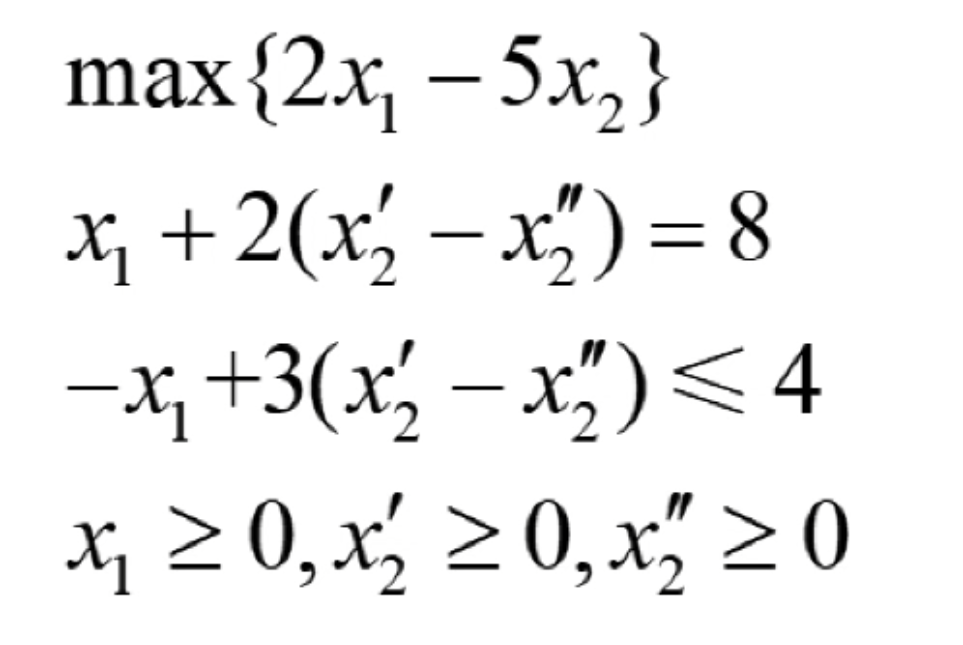
添加图片注释,不超过 140 字(可选)
而为了后续的算法设计的需要,还需要再作进一步的转换,那就是把所有小于等于的约束条件改为等于的约束条件,于是就有:
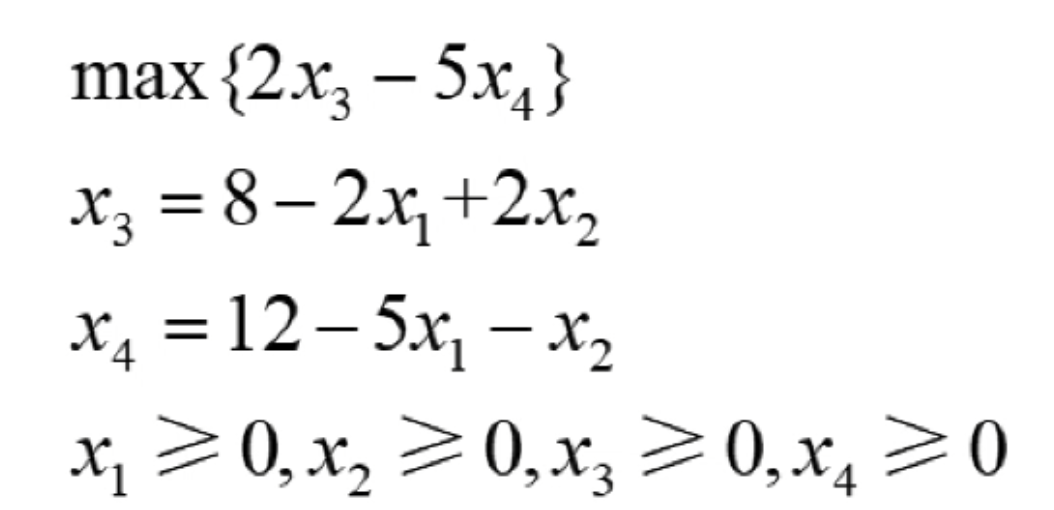
添加图片注释,不超过 140 字(可选)
对于以上的线性规划的系统当中,在等号的约束条件中等号左边的变量叫做基本元,等号右边的变量叫做非基本元,而且在实现的算法运行的过程当中,基本元和非基本元会不断地产生变化。
