考研第一天,汤家凤基础班,连续与极限复习笔记
函数连续极限
- 性质
- 保号性
- 证明极值点:
- 夹逼准则
- 二项式展开
- 根号下,大于一,小于一的讨论
- 直接放缩求和
- 分子分母齐次,且分母大一次,用积分
- 单调有界存在极限
- 几个重要的切线放缩
- 证明有界,然后放缩求单调
- 证明有界,然后相减求单调
- 无穷小
- 性质记忆
- 重要极限
- 重大考点不定型
- 零分之零
- 基本解法
- 注意无穷小的介
- 加减转化注意精确度
- 正常敏感变化:
- 注意ln()变化出一
- 对tan的不爽
- 分子有理化
- 一分之无穷
- 基本解法
- 例题
- 无穷分之无穷
- 基本解法
- 例题
- 零乘以无穷
- 转化为零比零 或者无穷比无穷就行
- 无穷减无穷
- 获得分母是求解的关键
- 提取公因试获得分母
- 分子有理化获得分母(注意技巧忽略小项)
- 通分获得分母
- 无穷分之零,零分之无穷
- 解题方法
- 例题
- 连续
- 间断点
- 例题
- 介值定理
- 存在函数区间,和函数求和,证明值存在
性质
保号性
证明极值点:
- 通过保号性,证明该点与附件的大小:
*
- 通过保号性确定附件导数的正负号:

夹逼准则
- 分子分母有一个不齐的时候用

二项式展开

根号下,大于一,小于一的讨论

直接放缩求和

分子分母齐次,且分母大一次,用积分
- 例题一,例题二:

单调有界存在极限
几个重要的切线放缩

证明有界,然后放缩求单调
- 例题一:

- 例题二:

证明有界,然后相减求单调

无穷小
性质记忆

重要极限

重大考点不定型

零分之零
基本解法
- 函数的指数函数 求e分之ln
- ln(…)------------>ln(1+…)~…
- (…)-1------------->
- e^a-1------------->a
- (1+a)^b---------------->ba
注意无穷小的介
- 这几个相减全为三阶
- 一个重要的 x减ln(x+1)

加减转化注意精确度

正常敏感变化:

注意ln()变化出一

对tan的不爽

分子有理化

一分之无穷
基本解法
- 转化为(1+0)^∞
- 恒等变化

例题

无穷分之无穷
基本解法
- 看增长速度 ,对数小于幂函数小于指数函数
- 看最高相次数
- (可能要洛必达)

例题
-
二项式定理

-
洛必达

- 除以,得到无穷小

零乘以无穷
转化为零比零 或者无穷比无穷就行
无穷减无穷
获得分母是求解的关键
提取公因试获得分母

分子有理化获得分母(注意技巧忽略小项)

通分获得分母

无穷分之零,零分之无穷
解题方法
- 直接e^ln()
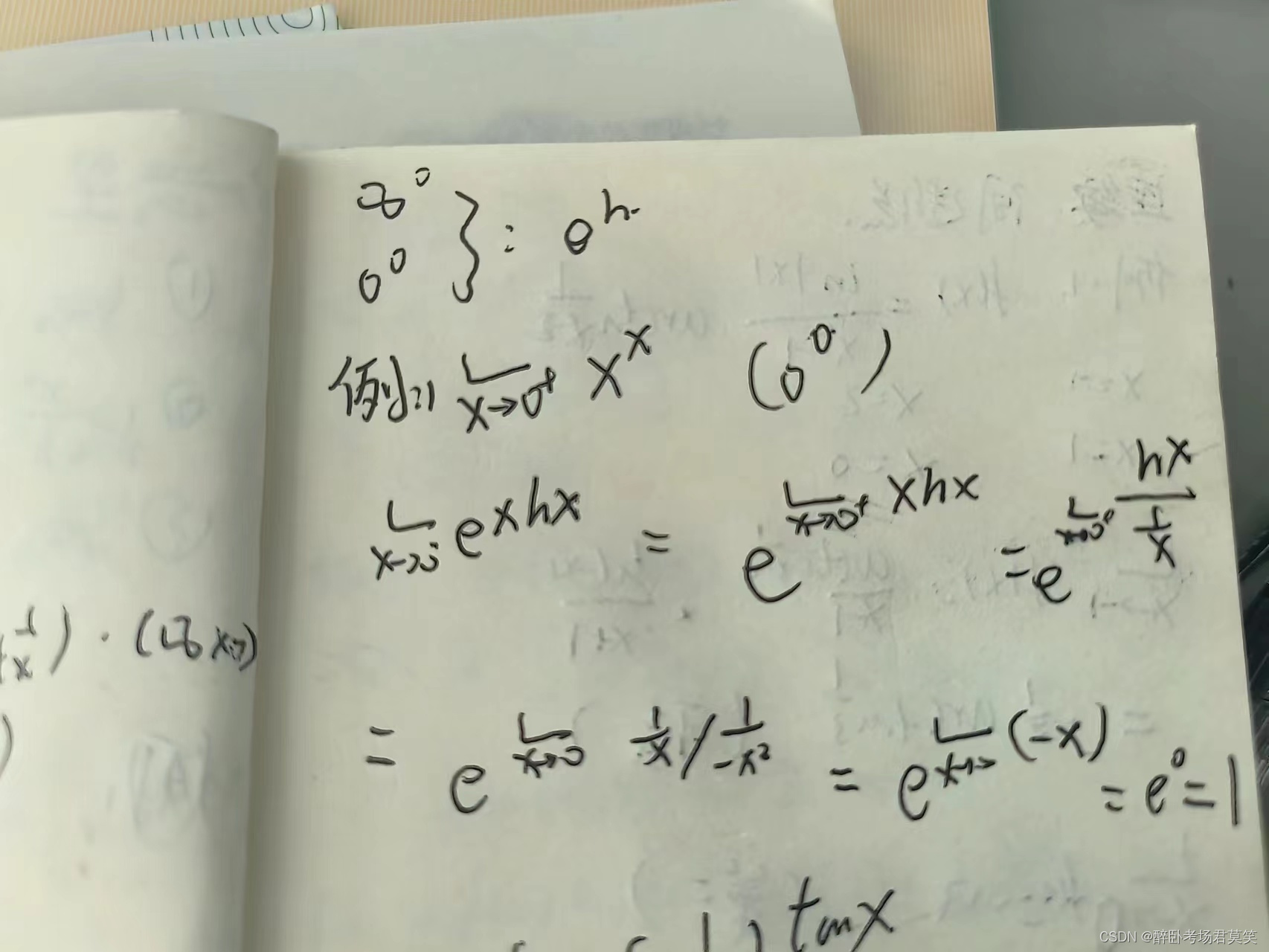
例题
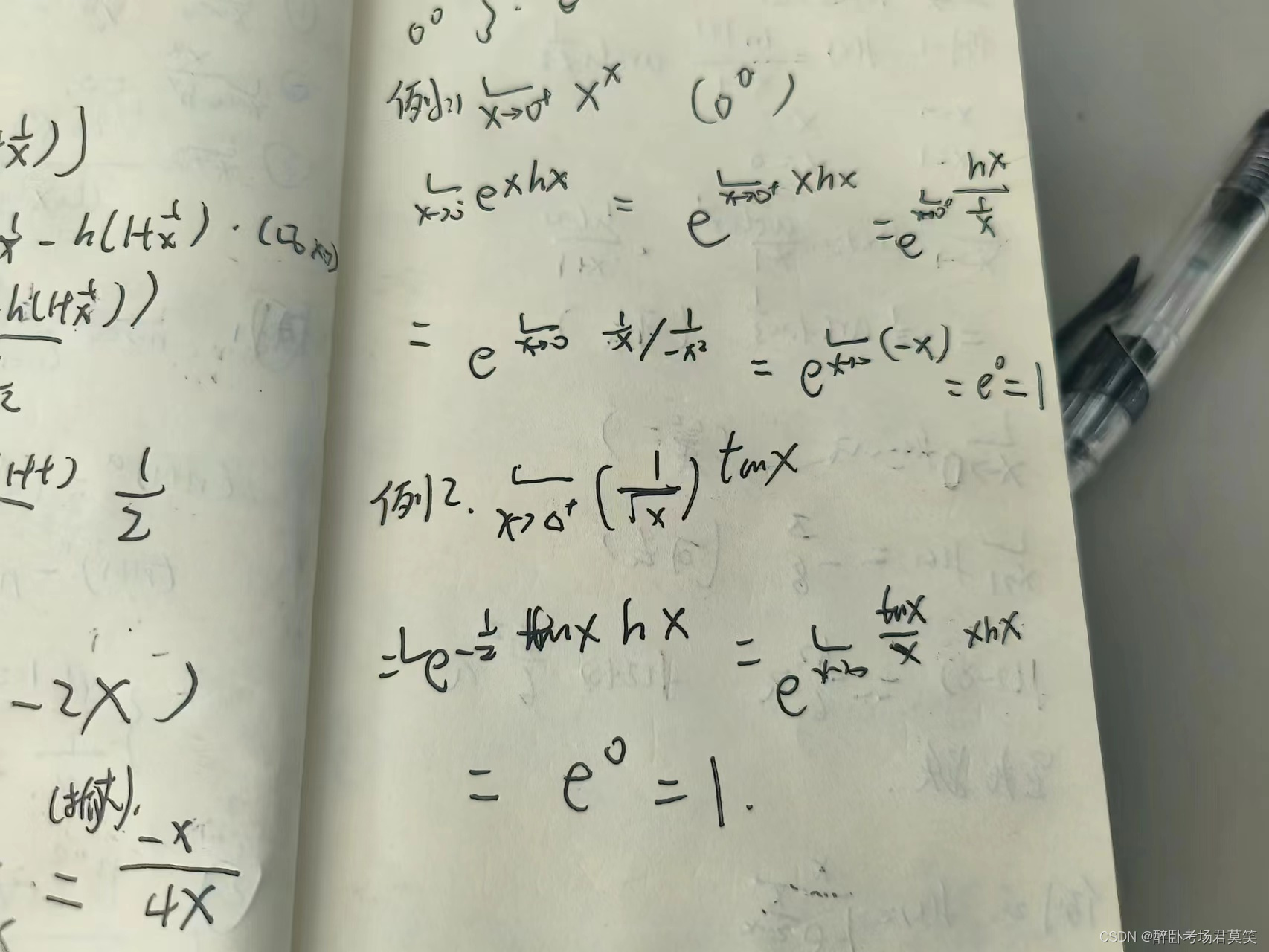
连续
间断点
- 找定义域中的间断点
- 左右极限相等就是可去
- 左右相等不相等就是跳跃
- 有无穷就是第二类

例题


介值定理
存在函数区间,和函数求和,证明值存在



