蒙特卡洛树搜索(MTCS)
一、目标
一种启发式的搜索算法,在搜索空间巨大的场景下比较有效
算法完成后得到一棵树,这棵树可以实现:给定一个游戏状态,直接选择最佳的下一步
二、算法四阶段
1、选择(Selection)
父节点选择UCB值最大的子节点作为当前节点
UCB=Vi‾+c2lnNniUCB=\overline{V_{i}} +c\sqrt{\frac{2lnN}{n_{i}}} UCB=Vi+cni2lnN
其中,c通常取2。
nin_{i}ni代表 iii 节点被选择的次数,NNN代表其父节点被选择的次数。
Vi‾\overline{V_{i}}Vi 代表 iii 节点的平均价值大小(例如 iii 节点 Vi=v,ni=3V_{i}=v,n_{i}=3Vi=v,ni=3,则Vi‾=v/3\overline{V_{i}}=v/3Vi=v/3)。
2、扩展(Expansion)
为当前节点创建一个或多个子节点(子节点代表当前节点下可采取的动作)
3、仿真(Simulation/Rollout)
在某一节点用随机策略进行模拟(rollout)
def Rollout(S_i): # S_i = 当前状态While True: # S_i达到终止条件/状态(下棋中某方获胜或平局)if S_i a terimal state: # 返回结果valuereturn value(S_i) # 还未终止,则# 随机选择一个当前状态下的可用动作A_i = random(available_action(S_i)) # 在当前状态下采取动作,得到新的状态S_i = simulate(A_i, S_i)
4、反向传播(Backpropagation)
得到模拟结果后不断反向更新父节点
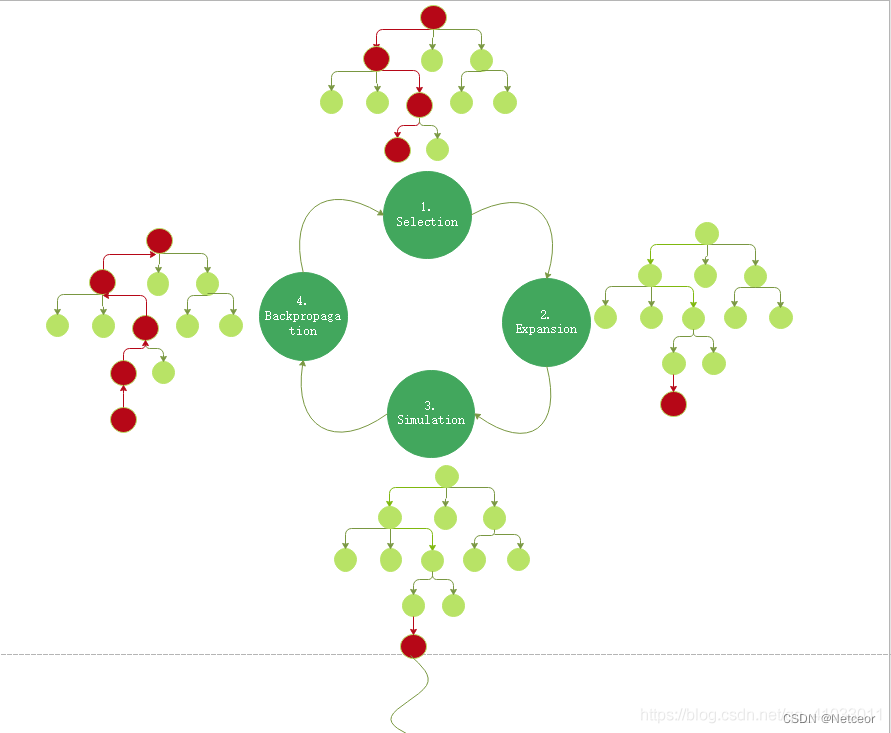
三、运行过程
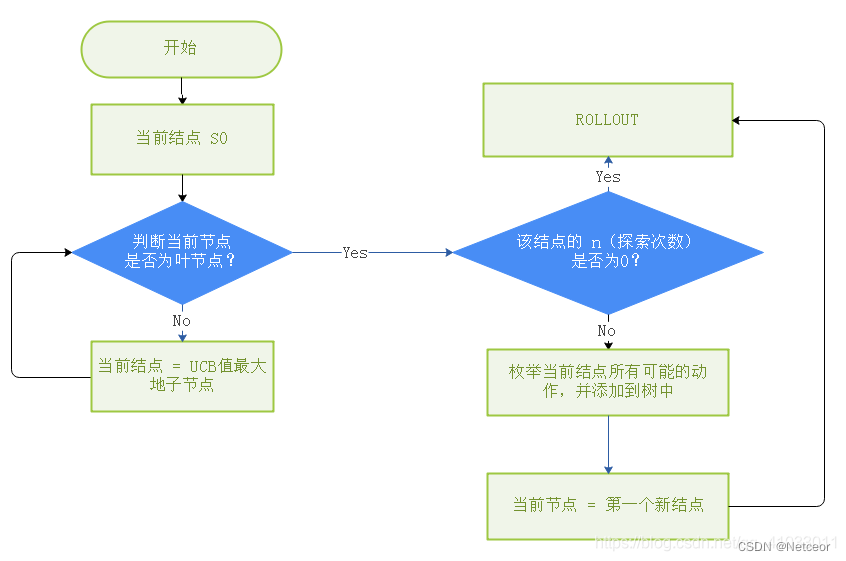
n代表当前节点被探索的次数。
则运行过程如下:
1、选择节点
- 当前节点是叶节点,则选择该节点
- 当前节点有孩子,孩子中UCB值最大的作为选择的节点
2、节点扩展 + 模拟
- 若选择的节点未模拟过(n=0),则进行模拟,得到结果后更新该节点 n=1 , value=结果数值。
- 若选择的节点模拟过(n≠0),则扩展节点。添加在该节点下所有可采取的动作,作为孩子
- 选择第一个孩子作为当前节点,进行模拟
def Rollout(S_i): # S_i = 当前状态While True: # S_i达到终止条件/状态(下棋中某方获胜或平局)if S_i a terimal state: # 返回结果valuereturn value(S_i) # 还未终止,则# 随机选择一个当前状态下的可用动作A_i = random(available_action(S_i)) # 在当前状态下采取动作,得到新的状态S_i = simulate(A_i, S_i)
3、反向传播
- 当孩子得到 Vc=v,nc+=1V_{c}=v,n_{c}+=1Vc=v,nc+=1,反向传播到父节点,父节点 Vp+=v,np+=1V_{p}+=v,n_{p}+=1Vp+=v,np+=1,直至传播到根节点。
三、实例
具体样例可参考博客蒙特卡洛树搜索(MCTS)详解、蒙特卡洛树搜索 MCTS 入门或b站视频AI如何下棋?直观了解蒙特卡洛树搜索MCTS!!!
