控制障碍函数(Control Barrier Function,CBF) 三、代码
三、代码实现
3.1、模型
这是一个QP问题,所以我们直接建模
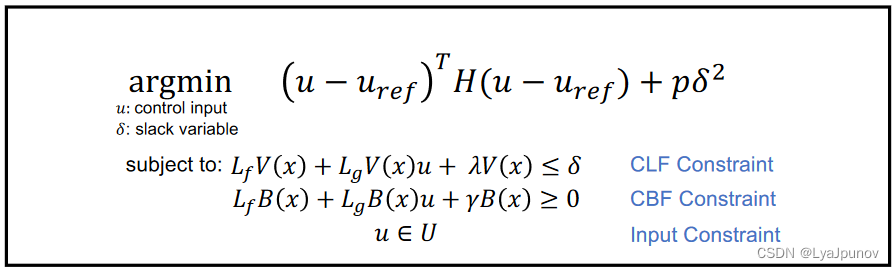
这其实还是之前的那张图,我们把这个大的框架带入到之前的那个小车追击的问题中去,得到以下的一些具体的约束条件
- CLF约束
L g V ( x ) u − δ ≤ − L f V ( x ) − λ V ( x ) L_g V(x) u - \delta \le - L_fV(x) - \lambda V(x) LgV(x)u−δ≤−LfV(x)−λV(x)
- CBF约束
− L g B ( x ) u ≤ L f B ( x ) + γ B ( x ) -L_g B(x) u \le L_fB(x) + \gamma B(x) −LgB(x)u≤LfB(x)+γB(x)
- 输入约束
u ≤ u m a x − u ≤ − u m i n \begin{aligned} u &\le u_{max} \\ -u &\le - u_{min} \end{aligned} u−u≤umax≤−umin
我们全部写成了这种小于等于的形式,便于下面的二次规划
3.2、实现
clc; clear; close all;dt = 0.02;
T = 30;
length = ceil(T ./ dt);sys.p = zeros(length,1); % 位置
sys.v = zeros(length,1); % 速度
sys.z = zeros(length,1); % 与前车距离
sys.u = zeros(length,1); % 控制量
sys.m = 1650; % 与系统相关参数
sys.g = 9.81;
sys.v0 = 14;
sys.vd = 24;
sys.f0 = 0.1;
sys.f1 = 5;
sys.f2 = 0.25;
sys.ca = 0.3;
sys.cd = 0.3;
sys.T = 1.8;
sys.u_max = sys.ca .* sys.m .* sys.g; % 控制量最大值
sys.u_min = - sys.cd .* sys.m .* sys.g; % 控制量最小值
sys.clf.rate = 5; % lambda
sys.cbf.rate = 5; % gamma
sys.wight.input = 2 ./ sys.m .^ 2; % 二次型矩阵H
sys.wight.slack = 2e-2; % 松弛变量系数 p% 状态初始化
sys.p(1,1) = 0;
sys.v(1,1) = 10;
sys.z(1,1) = 100;for i = 1:(length)t = i .* dt;p = sys.p(i,1);v = sys.v(i,1);z = sys.z(i,1);x = [p; v; z];F_r = sys.f0 + sys.f1.*v + sys.f2 .* v .* v;f = [v; - F_r ./ sys.m; sys.v0 - v];g = [0; 1./sys.m; 0];V = (v - sys.vd) .^ 2; % 李雅普诺夫函数dV = [0, 2 .* (v - sys.vd), 0]; % 李雅普诺夫函数的导LfV = dV * f; % 李导数LgV = dV * g;B = z - sys.T .* v - 0.5 .* (v - sys.v0) .^ 2 ./ (sys.cd .* sys.g); % 障碍函数dB = [0, - sys.T - (v - sys.v0) ./ sys.cd ./ sys.g, 0]; % 障碍函数的导LfB = dB * f; % 李导数LgB = dB * g;% 解控制量uA_ = [LgV, -1; -LgB, 0;1,0;-1,0];b_ = [-LfV - sys.clf.rate .* V; LfB + sys.cbf.rate .* B;sys.u_max;-sys.u_min;];H_ = [sys.wight.input, 0;0,sys.wight.slack];f_ = [- sys.wight.input * F_r; 0];u = quadprog(H_,f_,A_,b_);u = u(1); % 第二项是松弛变量,松弛变量这里也是一个待优化的值dx = f + g .* u;x_n = x + dx .* dt;% 保存数据sys.u(i,1) = u;sys.p(i+1,1) = x_n(1);sys.v(i+1,1) = x_n(2);sys.z(i+1,1) = x_n(3);
end% 绘图
figure(1);
subplot(4,1,1);
plot(dt:dt:T,sys.p(1:length,:));
ylabel('p')subplot(4,1,2);
plot(dt:dt:T,sys.v(1:length,:));
ylabel('v')subplot(4,1,3);
plot(dt:dt:T,sys.z(1:length,:));
ylabel('z')subplot(4,1,4);
plot(dt:dt:T,sys.u);
ylabel('u')
这里我们的二次规划求解器用到了Matlab中的函数quadprog,其文档地址为 https://ww2.mathworks.cn/help/optim/ug/quadprog.html
本文的结果为
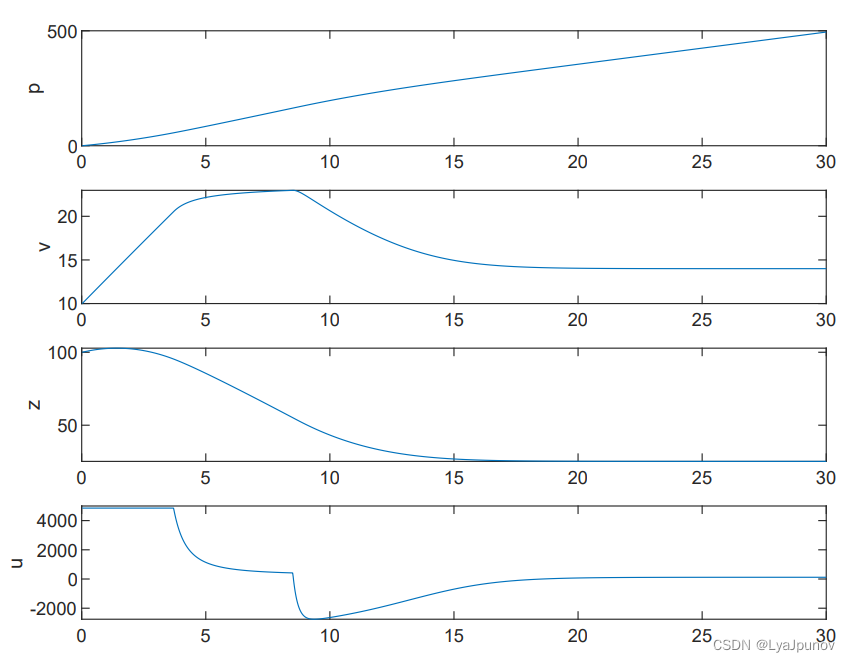
相较于作者给出的代码,本文的代码更加简单,适合初学者使用
