2702 高级打字机
因为Undo操作只能撤销Type操作,所以Undo x 实际上就是删除文章末尾x个字母。用一个栈即可解决(每个字母最多进出一次)。
这种情况下只需要设计一个合理的数据结构依次执行操作即可。
版本树:Undo x撤销最近的x次修改操作,实际上就是当前版本还原为x次操作前的版本,换句话说,版本i = 版本i-x-1。
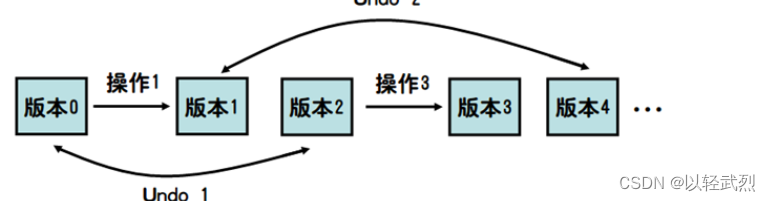
如图所示,所有版本呈树状排列,版本0为根。
读入所有操作并建树,对这颗版本树按欧拉序求出所有版本。上图中就是按0->1->4…4->1->0->2->3->2->0的顺序遍历,同样使用栈就能计算出所有的版本,然后在对应的版本上解决询问即可。
到此,就得到了时空复杂度均为O(n)的离线算法。
能解决这类题目的条件是:
1.允许使用离线算法,进而求出版本树,并允许把询问挂到树的节点上。
2.所有操作都是可逆的。只有所有操作都是可逆的,才能按欧拉序依次求出各版本。如本题的Type操作的逆操作就是弹出栈顶,Undo操作则根本不需要修改(Undo前后2个版本相同)。
#include<cstdio>
using namespace std;
const int R=1e5,N=(R+1)*20;
int n,m,now,sz,root[R+1],ls[N],rs[N],len[N];
char s[N];
inline int read(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}return x*f;
}
void insert(int &k,int last,int l,int r,int pos,int c){k=++sz;if(l==r){s[k]=c;return ;}ls[k]=ls[last];rs[k]=rs[last];int mid=l+r>>1;if(pos<=mid) insert(ls[k],ls[last],l,mid,pos,c);else insert(rs[k],rs[last],mid+1,r,pos,c);
}
void query(int &k,int last,int l,int r,int pos){if(l==r){putchar(s[k]);putchar('\n');return ;}int mid=l+r>>1;if(pos<=mid) query(ls[k],ls[last],l,mid,pos);else query(rs[k],rs[last],mid+1,r,pos);
}
int main(){n=read();for(int i=1,x;i<=n;i++){char op=0,ch=0;for(;op<'A'||op>'Z';op=getchar());if(op=='T'){for(;ch<'a'||ch>'z';ch=getchar());now++;len[now]=len[now-1]+1;insert(root[now],root[now-1],1,R,len[now],ch);}else if(op=='U'){x=read();now++;root[now]=root[now-x-1];len[now]=len[now-x-1];}else x=read(),query(root[now],root[now-1],1,R,x);}return 0;
}