最短路径(数据结构实训)(难度系数100)
最短路径
描述:
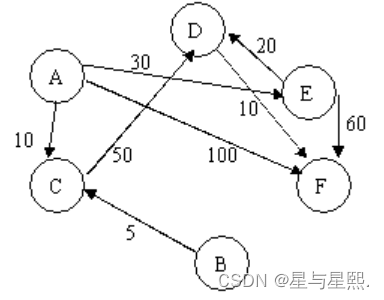
已知一个城市的交通路线,经常要求从某一点出发到各地方的最短路径。例如有如下交通图:
则从A出发到各点的最短路径分别为:
B:0
C:10
D:50
E:30
F:60输入:
输入只有一个用例,第一行包括若干个字符,分别表示各顶点的名称,接下来是一个非负的整数方阵,方阵维数等于顶点数,其中0表示没有路,正整数表示两点之间边的长度。可以假定该图为有向图。
最后一行为要求的出发点。输出:
输出从已知起点到各顶点的最短路径长度。输出格式是根据顶点输入顺序,依次输出其最智短路径长度。各顶点分别用一行输出,先输出目标顶点,然后一冒号加一个空格,最后是路径长度。0表示没有路。
样例输入:
ABCDEF
0 0 10 0 30 100
0 0 5 0 0 0
0 0 0 50 0 0
0 0 0 0 0 10
0 0 0 20 0 60
0 0 0 0 0 0
A
样例输出:
B: 0
C: 10
D: 50
E: 30
F: 60
方法一(Floyd算法):
import java.util.Scanner;public class Xingyuxingxi
{public static void main(String[] args){Scanner sc=new Scanner(System.in);String str=sc.next();int n=str.length();int [][]dt=new int[n][n];for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {dt[i][j]=sc.nextInt();if(dt[i][j]==0&&i!=j) {dt[i][j]=5000000;//因为题目数据范围有限,所以用5000000代替最大值,也可以用别的数代替}}}char a=sc.next().charAt(0);for(int k=0;k<n;k++){//floyd算法的简单之处,只需要三层循环,就能遍历出所有点到所有点的最短距离,如果范围过大就不要用floyd算法了for(int i=0;i<n;i++){for(int j=0;j<n;j++){dt[i][j]=Math.min(dt[i][j],dt[i][k]+dt[k][j]);//更新最短路径}}}int g=0;for(int i=0;i<n;i++) {if(str.charAt(i)==a) {//找到起始点的下标g=i;break;}}for (int i = 0; i < n; i++) {if(dt[g][i]==5000000)dt[g][i]=0;//如果为最大值表示没有路,题目要求用0表示没有路if(str.charAt(i)!=a)//如果不是起始点则输出最短距离System.out.printf("%c: %d\n",str.charAt(i),dt[g][i]);}}
}方法二(Dijkstra算法):
import java.util.Scanner;public class Xingyuxingxi
{public static void main(String[] args){Scanner sc=new Scanner(System.in);String str=sc.next();int n=str.length();int [][]dt=new int[n][n];int []dist=new int[n];//储存选定起点到其他点的距离boolean []st=new boolean[n];//储存该点是否遍历过到其他点的距离for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {dt[i][j]=sc.nextInt();if(dt[i][j]==0&&i!=j) {dt[i][j]=5000000;//用5000000代替最大值Integer.MAX_VALUE}}}char a=sc.next().charAt(0);for (int i = 0; i < n; i++) {dist[i]=5000000;}int g=0;for(int i=0;i<n;i++) {if(str.charAt(i)==a){//找到起点下标g=i;break;}}dist[g]=0;for (int i = 0; i < n; i++) {int t=-1;for(int j=0;j<n;j++) {if(!st[j]&&(t==-1||dist[t]>dist[j])){//找到每次更新路线后t到起点的最短距离的点t=j;}}st[t]=true;for(int j=0;j<n;j++){//更新距离,各个点到t的距离dist[j]=Math.min(dist[j],dist[t]+dt[t][j]);}}for (int i = 0; i < n; i++) {if(dist[i]==5000000)dist[i]=0;//如果为最大值表示没有路,题目要求用0代替没有通路if(i!=g)System.out.printf("%c: %d\n",str.charAt(i),dist[i]);}}
}关于为什么用5000000代替Integer.MAX_VALUE
因为题目中涉及到最大值的计算,如果使用Integer.MAX_VALUE加任意一个数的话就会变为负数,求最小值的话就会一直是Integer.MAX_VALUE+其他数的和,我自己写的时候每次加都会变成负数,所以就把最大值改小了,本题数据并不强,可以用一个足够大的数代替这个最大值即可,不一定非得是5000000