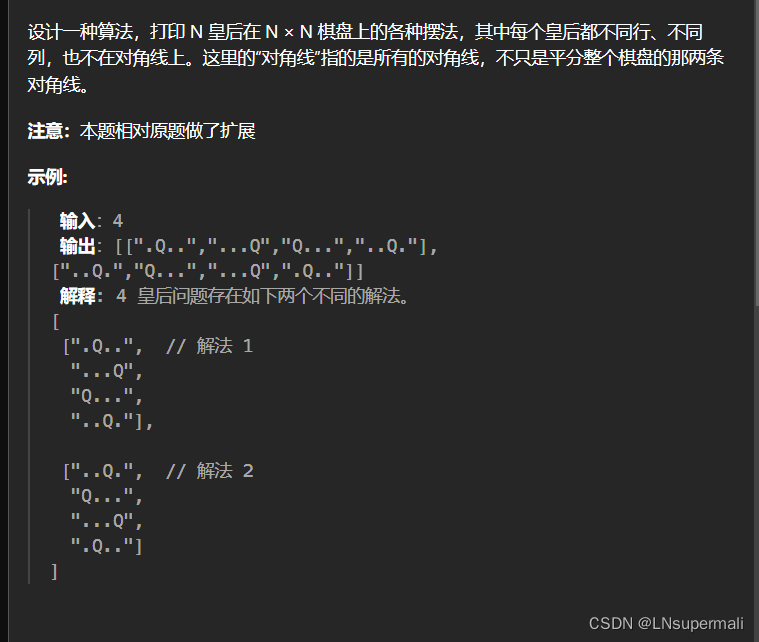
力扣面试题 08.12. 八皇后(java回溯解法)
Problem: 面试题 08.12. 八皇后
文章目录
- 题目描述
- 思路
- 解题方法
- 复杂度
- Code
题目描述
思路
八皇后问题的性质可以利用回溯来解决,将大问题具体分解成如下待解决问题:
1.以棋盘的每一行为回溯的决策阶段,判断当前棋盘位置能否放置棋子
2.如何判断当前棋盘位置是否可以放置棋子
解题方法
1.回溯函数:
1.1定义二维结果集result,char类型二维数组(作为棋盘)并初始化
1.2当决策阶段row等于n时,将当前的决策路径添加到result中(注意决策阶段应该等于n时才说明将棋盘判断完了,因为当决策阶段等于n时说明0 - n-1 已经判断处理完)
1.3由于在每一个决策阶段我们需要对棋盘的每一列棋格判断(穷举),所以以每一列为循环判断(调用判断当前位置是否可以添加棋子的函数),若可以则先将棋盘当前位置添上棋子,再回溯判断当前行的下一行,判断完当前行后还需恢复当前棋盘位置的状态
2.判断当前位置是否可以添加棋子函数
2.1依次利用循环判断当前位置的列,右上角,左上角是否存在棋子,存在则不可在当前位置添加棋子
复杂度
时间复杂度:
O ( n ! ) O(n!) O(n!)
空间复杂度:
O ( n ) O(n) O(n)
Code
class Solution {//Two-dimensional result setprivate List<List<String>> result = new ArrayList<>();/*** Get the solution to the Eight Queens problem** @param n The size of board* @return List<List < String>>*/public List<List<String>> solveNQueens(int n) {char[][] board = new char[n][n];for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {board[i][j] = '.';}}backtrack(0, board, n);return result;}/*** Find the solution of the eight queens problem by backtracking** @param board Board* @param row The row of board(The decision stage of backtracking)* @param n The size of board*/private void backtrack(int row, char[][] board, int n) {//End condition:A feasible solution is foundif (row == n) {List<String> snapshot = new ArrayList<>();for (int i = 0; i < n; ++i) {snapshot.add(new String(board[i]));}result.add(snapshot);return;}//Each has n ways to placefor (int col = 0; col < n; ++col) {if (isOk(board, n, row, col)) {//optional list//The chess board places pieces in row rows and col columnsboard[row][col] = 'Q';//Investigate the next rowbacktrack(row + 1, board, n);//Recover the selectionboard[row][col] = '.';}}}/*** Determines whether the current column can place chess pieces** @param board The board* @param n The row number and column number of board* @param row The row number of board* @param col The column number of board* @return boolean*/private boolean isOk(char[][] board, int n, int row, int col) {//Check whether columns conflictfor (int i = 0; i < n; ++i) {if (board[i][col] == 'Q') {return false;}}//Check whether top right corner conflictint i = row - 1;int j = col + 1;while (i >= 0 && j < n) {if (board[i][j] == 'Q') {return false;}i--;j++;}//Check whether top left corner conflicti = row - 1;j = col - 1;while (i >= 0 && j >= 0) {if (board[i][j] == 'Q') {return false;}i--;j--;}return true;}
}