通信原理板块——线性分组码之汉明码
微信公众号上线,搜索公众号小灰灰的FPGA,关注可获取相关源码,定期更新有关FPGA的项目以及开源项目源码,包括但不限于各类检测芯片驱动、低速接口驱动、高速接口驱动、数据信号处理、图像处理以及AXI总线等

1、汉明码
(1)常见概念
代数码,是指建立在代数学基础上的编码,常用的是线性码。
线性码,是指按照一组线性方程构成的编码,线性码中信息位和监督位是由一些线性代数方程联系着。
汉明码是一种能够纠正1位错码且编码效率较高的线性分组码。
(2)汉明码的构造原理
若码长为n,信息位数为k,则监督位数为n-k;如果希望用r个监督位构造出r个监督关系式来指示一位错码的n种可能位,则要求:
2^ r-1≥n或2^ r≥k+r+1
一位监督码a0和信息位an-1……a1一起构成偶数监督码的代数式
an-1⊕an-2⊕……⊕a0=0
在接收端解码时,需要根据监督关系式,计算校正子S
监督关系式:S=an-1⊕an-2⊕……⊕a0
因为校正子S只有一位,只能代表有错和无措两种信息
若S=0,则无错码;若S=1,则有错码
两位校正子即2个监督关系式,共四种组合00,01,10,11,可以表示四种不同的信息,可以指示一个错码的3种不同位置
故若r个校正子,即r个监督关系式,能指示一个错码的(2^r-1)个位置。
(3)构造监督关系式和汉明码
设分组码(n,k)中k=4,为了纠正一位错码,要求监督位数r≥3。
令r=3,则n=k+r=7,用a6,a5,a4,a3,a2,a1,a0表示这7个码元,用S1,S2,S3表示3个监督关系式中的校正子,规定S1,S2,S3的值与错码位置的关系如下表,
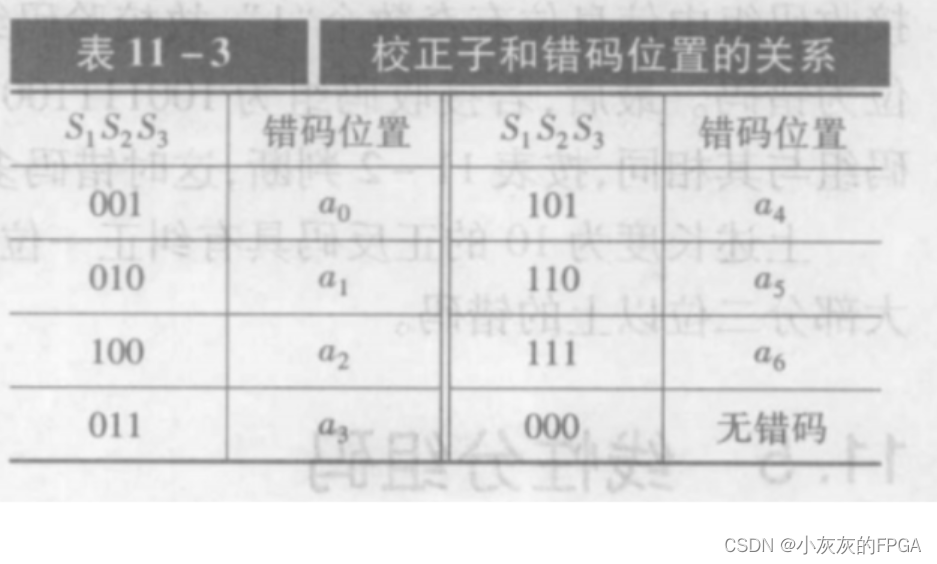
仅当错码位置在a6,a5,a4或a2时,S1=1,由此构成偶数监督关系:
S1=a6⊕a5⊕a4⊕a2
仅当错码位置在a6,a5,a3或a1时,S2=1,由此构成偶数监督关系:
S2=a6⊕a5⊕a3⊕a1
仅当错码位置在a6,a4,a3或a0时,S3=1,由此构成偶数监督关系:
S3=a6⊕a4⊕a3⊕a0
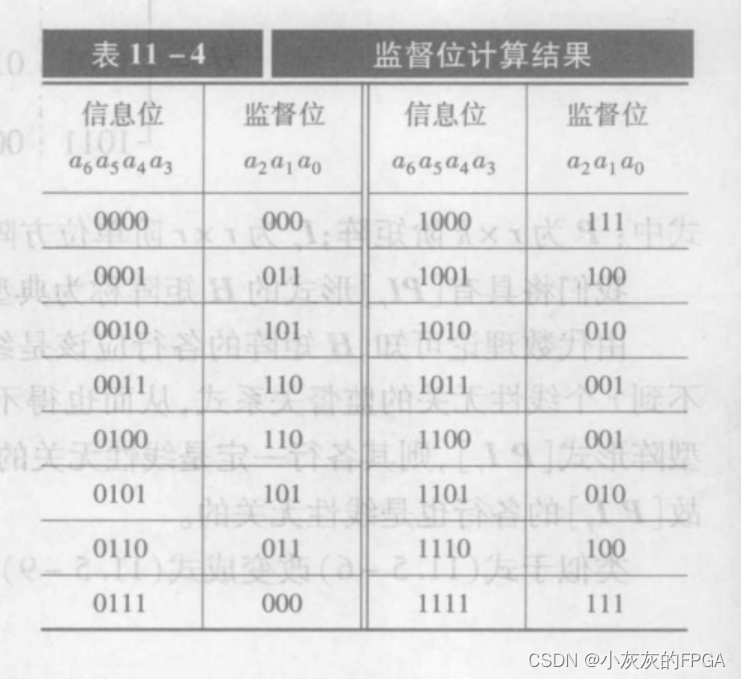
当发送端编码时,信息位a6,a5,a4,a3是随机输入的,而监督位a2,a1,a0根据信息位的取值,按照监督关系式来确定,要求编码中无错码则需要保持S1,S2,S3的值均为0,故:
a6⊕a5⊕a4⊕a2=0
a6⊕a5⊕a3⊕a1=0
a6⊕a4⊕a3⊕a0=0
由此可得出:
a2=a6⊕a5⊕a4
a1=a6⊕a5⊕a3
a0=a6⊕a4⊕a3
由此可构造出汉明码
2、线性分组码的原理证明
线性码时信息位和监督位满足一组线性代数方程式的码
取一组线性方程式
(1×a6)⊕(1×a5)⊕(1×a4)⊕(0×a3)⊕(1×a2)⊕(0×a1)⊕(0×a0)=0
(1×a6)⊕(1×a5)⊕(0×a4)⊕(1×a3)⊕(0×a2)⊕(1×a1)⊕(0×a0)=0
(1×a6)⊕(0×a5)⊕(1×a4)⊕(1×a3)⊕(0×a2)⊕(0×a1)⊕(1×a0)=0

H—监督矩阵(parity-check matrix)
若监督矩阵H确定,则编码时监督位和信息位的关系就完全确定。

具有[PIr]形式的H矩阵称为典型阵。

在信息位给定后,用信息位的行矩阵乘矩阵Q产生监督位。
在Q的左边加上k×k阶单位矩阵,构成矩阵G

具有[IkQ]形式的生成矩阵称为典型生成矩阵G
由典型生成矩阵得出的码组A中,信息位的位置不变,监督位附加于其后,这种形式的码称为系统码
