当前位置： 首页 > news >正文

【数据结构与算法】前缀树的实现

news 2025/7/9 0:24:53

🌠作者：@阿亮joy.
🎆专栏：《数据结构与算法要啸着学》
🎇座右铭：每个优秀的人都有一段沉默的时光，那段时光是付出了很多努力却得不到结果的日子，我们把它叫做扎根
在这里插入图片描述


目录

    • 👉前缀树的实现👈
      • 什么是前缀树
      • 节点的定义
      • 构造函数
      • 插入字符串
      • 查找字符串和前缀
      • 析构函数
      • 删除字符串
      • 打印前缀树
      • 完整代码
      • OJ题：实现前缀树
    • 👉总结👈

👉前缀树的实现👈

什么是前缀树

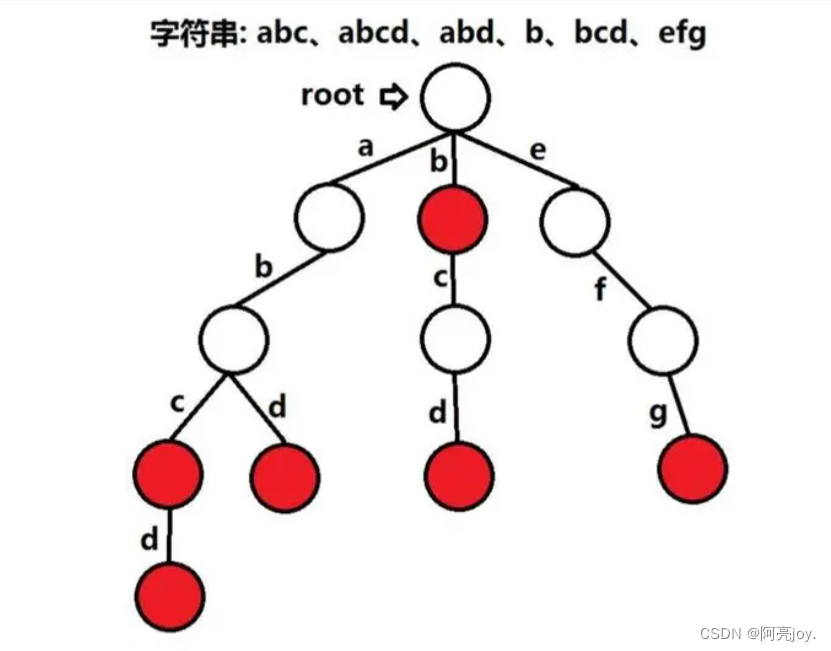
Trie（发音类似 “try”），被称为前缀树或字典树，是一种树形的数据结构，可用于高效地存储和检索字符串数据集中的键。这个数据结构有相当多的应用情景，例如自动补完和拼写检查。下图就是经典的前缀树，我们接下来要实现的前缀树的节点存储的数据比较丰富，以达到特定字符串在树中出现几次等类似的功能。

在这里插入图片描述

节点的定义

// 前缀树节点的定义
// 假设字符都是小写字母
struct TrieNode
{int pass = 0;	// 有几个字符串经过该节点(前缀包含这个字符的字符串数量)int end = 0;	// 以该节点为结尾的字符串的数量,如果不允许字符串重复插入,可以改成bool// next[0] == nullptr 表示没有走向'a'的路// next[0] != nullptr 表示有走向'a'的路// ...// next[25] != nullptr 表示有走向'z'的路TrieNode* next[26] = { nullptr };	// 26个空位,准备挂下一个节点'a'-'z',没有挂节点时为nullptr// 如果字符种类个数比较多,可以将数组换成哈希表或者set
};

构造函数

前缀树是用哨兵位头节点来管理整棵前缀树的，所以其构造函数需要 new 上一个哨兵位头节点。

class Trie
{typedef TrieNode Node;
public:Trie(){_root = new Node();}
private:Node* _root = nullptr;	// 哨兵位头节点,可以用来求前缀树中字符串的数量,也可以求空串的数量
};

注：哨兵位头节点的 pass 值可以表示前缀树含有的字符串数量，end 值可以表示前缀树含有空串的数量。因为任何字符串都会以空串作为前缀，都会经过哨兵位头节点。

插入字符串

我们从哨兵位头节点开始，插入字符串。对于当前字符对应的子节点，有以下两种情况：

  • 子节点存在：沿着指针移动到子节点，继续处理下一个字符。
  • 子节点不存在：创建一个新的子节点，记录在 next 指针数组的对应的位置上，然后沿着指针移动到子节点，继续处理下一个字符。
  • 插入字符串的同时，还需要更新沿途节点的 pass 值。

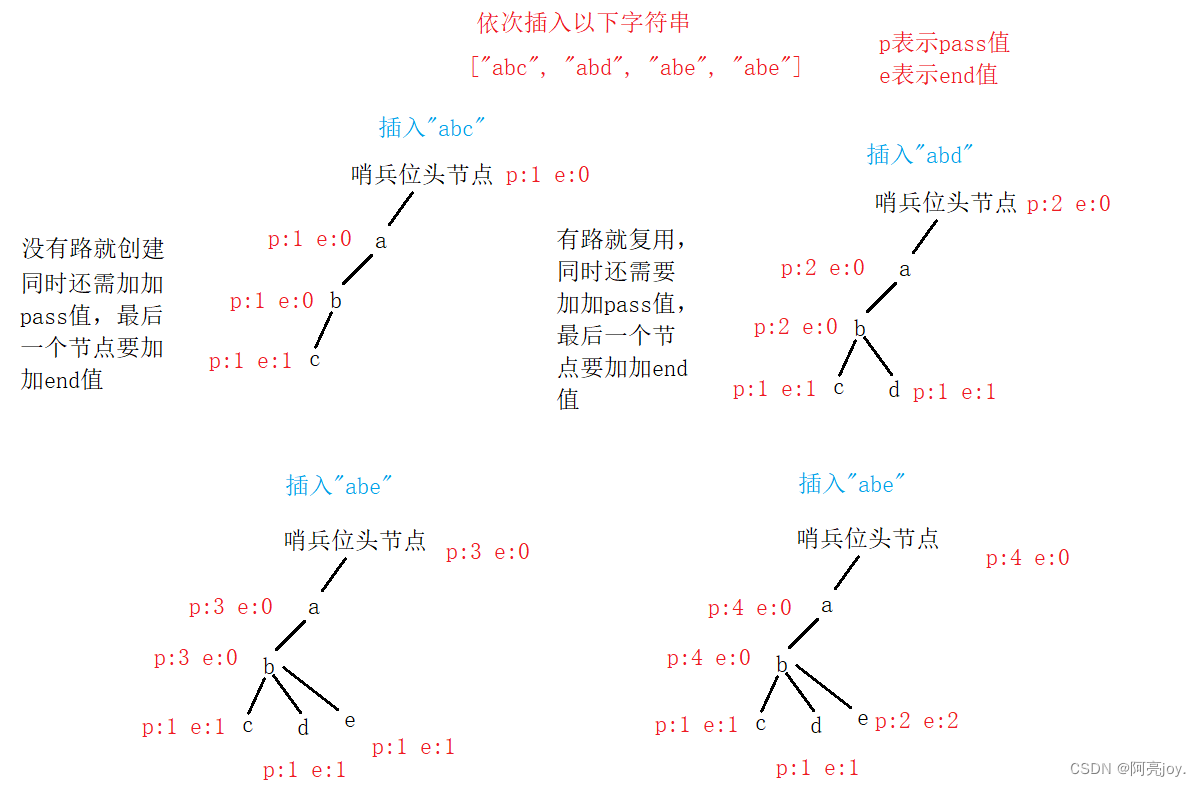
插入字符串图解：

在这里插入图片描述

class Trie
{
public:void Insert(const string& str){Node* cur = _root;++cur->pass;	// 任何一个字符串都需要经过哨兵位头节点for (size_t i = 0; i < str.size(); ++i){size_t index = str[i] - 'a';// 如果之前没有字符串经过该节点,则需要建出新节点if (cur->next[index] == nullptr){cur->next[index] = new Node();}cur = cur->next[index];++cur->pass;}// cur指向字符串的最后一个节点,++cur->end表示多了一个字符串以该节点结尾++cur->end;}
}

如果不需要插入重复字符串，可以将函数的返回值改成 bool 类型。

查找字符串和前缀

class Trie
{
public:// 查找前缀树中有多少个要查找的字符串size_t Search(const string& str) const{Node* cur = _root;for (auto ch : str){// 找的过程发现没路了,说明树中不存在要查找的字符串if (cur->next[ch - 'a'] == nullptr){return 0;}cur = cur->next[ch - 'a'];}// cur是str最后一个字符,cur->end表示树中有多少个strreturn cur->end;}// 查找树中有多少个字符串以前缀prefix为前缀size_t StartsWith(const std::string& prefix) const{Node* cur = _root;for (auto ch : prefix){// 找的过程中发现没有路,则说明没有字符串以prefix为前缀if (cur->next[ch - 'a'] == nullptr){return 0;}cur = cur->next[ch - 'a'];}// cur->pass表示有多少个字符串以prefix为前缀return cur->pass;}
}

注：查找的过程和插入的过程非常的相似，只是查找时发现没有路，就直接返回 0，表示树中没有该字符串或者树中的字符串不以 prefix 为前缀。注：如果树中有要查找的字符串 str，则 cur->end 表示树中有多少个 str；如果树有字符串以 prefix 为前缀，则 cur->pass 表示多少个字符串以 prefix 为前缀。

析构函数

class Trie
{typedef TrieNode Node;
public:~Trie(){Destroy(_root);}
private:void Destroy(Node* root){// 先销毁孩子节点,才能够销毁自己for (int i = 0; i < 26; ++i){// root->next[i]不为空,则说明有节点,需要递归释放节点if (root->next[i] != nullptr){Destroy(root->next[i]);}}delete root;}
}

前缀树析构时，需要先释放孩子节点，才能够释放哨兵位头节点。而孩子节点有可能会有孩子节点，所以我们可以采用递归去释放节点。

删除字符串

class Trie
{typedef TrieNode Node;
public:// 从树中删除字符串str,注：如果有多个str,只会删除一次void Erase(const string& str){// 树中没有str,无法删除if (Search(str) == 0)return;Node* cur = _root;--cur->pass;for (size_t i = 0; i < str.size(); ++i){size_t index = str[i] - 'a';// 如果发现str是唯一经过该节点的字符串// 那么就需要递归去释放当前节点及后续路径的节点if (--cur->next[index]->pass == 0){Destroy(cur->next[index]);	// 递归释放节点cur->next[index] = nullptr;	// next需要置为nullptrreturn;}cur = cur->next[index];}// 如果字符串的所有字符都删除了一遍,还有该路径,那么最后要// --cur->end,表明树中str的个数减少了一个--cur->end;}
}

删除字符串时，需要看树中是否有需要删除的字符串。如果没有，直接 return 即可。如果有，才进行删除。进行删除时，如果发现 str 是唯一经过该节点的字符串，那么就需要递归去释放当前节点及后续路径的节点。

打印前缀树

class Trie
{typedef TrieNode Node;
public:void Print() const{cout << "根节点:[" << "pass: " << _root->pass << " end: " << _root->end << "]" << endl;_Print(_root);}
private:void _Print(Node* root) const{if (root == nullptr)return;for (int i = 0; i < 26; ++i){if (root->next[i] == nullptr)continue;else{cout << "节点" << (char)('a' + i) << ":[pass: " << root->next[i]->pass << " end: " << root->next[i]->end << "]" << endl;_Print(root->next[i]);}}}
}

完整代码

#pragma once#include <vector>
#include <string>
#include <iostream>
using namespace std;// 前缀树节点的定义
// 假设字符都是小写字母
struct TrieNode
{int pass = 0;	// 有几个字符串经过该节点(前缀包含这个字符的字符串数量)int end = 0;	// 以该节点为结尾的字符串的数量,如果不允许重复插入,可以改成bool// next[0] == nullptr 表示没有走向'a'的路// next[0] != nullptr 表示有走向'a'的路// ...// next[25] != nullptr 表示有走向'z'的路TrieNode* next[26] = { nullptr };	// 26个空位,准备挂下一个节点'a'-'z',没有挂节点时为nullptr// 如果字符种类个数比较多,可以将数组换成哈希表或者set
};class Trie
{typedef TrieNode Node;
public:Trie(){_root = new Node();}~Trie(){Destroy(_root);}// 查找前缀树中有多少个要查找的字符串size_t Search(const string& str) const{Node* cur = _root;for (auto ch : str){// 找的过程发现没路了,说明树中不存在要查找的字符串if (cur->next[ch - 'a'] == nullptr){return 0;}cur = cur->next[ch - 'a'];}// cur是str最后一个字符,cur->end表示树中有多少个strreturn cur->end;}// 查找树中有多少个字符串以前缀prefix为前缀size_t StartsWith(const std::string& prefix) const{Node* cur = _root;for (auto ch : prefix){// 找的过程中发现没有路,则说明没有字符串以prefix为前缀if (cur->next[ch - 'a'] == nullptr){return 0;}cur = cur->next[ch - 'a'];}// cur->pass表示有多少个字符串以prefix为前缀return cur->pass;}// 插入字符串void Insert(const string& str){Node* cur = _root;++cur->pass;	// 任何一个字符串都需要经过哨兵位头节点for (size_t i = 0; i < str.size(); ++i){size_t index = str[i] - 'a';// 如果之前没有字符串经过该节点,则需要建出新节点if (cur->next[index] == nullptr){cur->next[index] = new Node();}cur = cur->next[index];++cur->pass;}// cur指向字符串的最后一个节点,++cur->end表示多了一个字符串以该节点结尾++cur->end;}// 从树中删除字符串str,注：如果有多个str,只会删除一次void Erase(const string& str){// 树中没有str,无法删除if (Search(str) == 0)return;Node* cur = _root;--cur->pass;for (size_t i = 0; i < str.size(); ++i){size_t index = str[i] - 'a';// 如果发现str是唯一经过该节点的字符串// 那么就需要递归去释放当前节点及后续路径的节点if (--cur->next[index]->pass == 0){Destroy(cur->next[index]);	// 递归释放节点cur->next[index] = nullptr;	// next需要置为nullptrreturn;}cur = cur->next[index];}// 如果字符串的所有字符都删除了一遍,还有该路径,那么最后要// --cur->end,表明树中str的个数减少了一个--cur->end;}void Print() const{cout << "根节点:[" << "pass: " << _root->pass << " end: " << _root->end << "]" << endl;_Print(_root);}private:void Destroy(Node* root){// 先销毁孩子节点,才能够销毁自己for (int i = 0; i < 26; ++i){if (root->next[i] != nullptr){Destroy(root->next[i]);}}delete root;}void _Print(Node* root) const{if (root == nullptr)return;for (int i = 0; i < 26; ++i){if (root->next[i] == nullptr)continue;else{cout << "节点" << (char)('a' + i) << ":[pass: " << root->next[i]->pass << " end: " << root->next[i]->end << "]" << endl;_Print(root->next[i]);}}}private:Node* _root = nullptr;	// 哨兵位头节点,可以用来求前缀树中字符串的数量,也可以求空串的数量
};

前缀树的测试

void TrieTest()
{Trie t;vector<string> v = { "abc","abd", "abe", "abe", "" ,"a" , "bc", "bd", "be" };for (string& str : v){t.Insert(str);}// 前缀树的打印t.Print();cout << "----------------------" << endl;// 输出空串的数量cout << "空串的数量: " << t.Search("") << endl;// 任意字符串均以空串为前缀/树中字符串的数量cout << "树中字符串的数量: " << t.StartsWith("") << endl;// 以"ab"为前缀的字符串个数cout << "以ab为前缀的字符串个数: " << t.StartsWith("ab") << endl;cout << "----------------------" << endl;// 测试删除for (string& str : v){t.Erase(str);}t.Print();
}

在这里插入图片描述

OJ题：实现前缀树

这里是引用

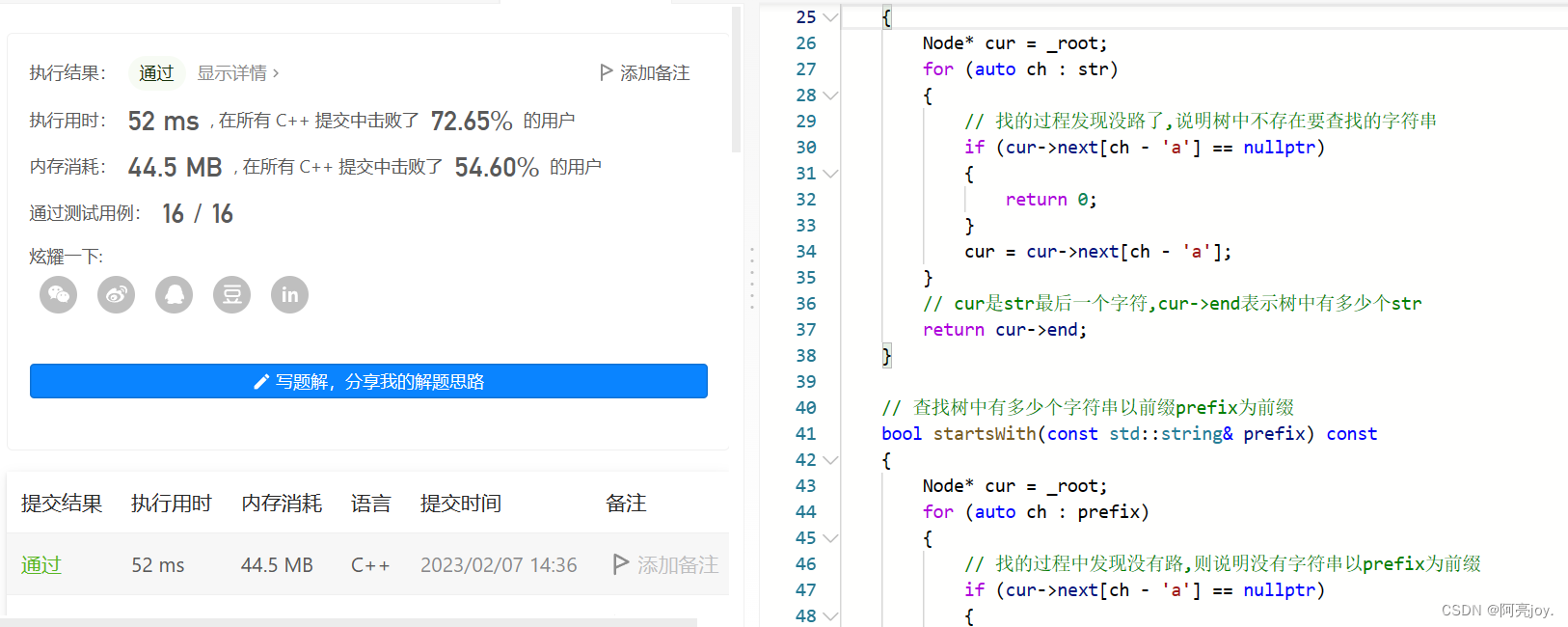
LeetCode 上的实现前缀树是比我们实现的前缀树是要难度低的，所以只需要将上面的代码拷贝过去，再将函数名和函数的返回值修改成题目要求的样子就可以通过了。

在这里插入图片描述

👉总结👈

本篇博客主要讲解了什么是前缀树以及前缀树的实现等。那么以上就是本篇博客的全部内容了，如果大家觉得有收获的话，可以点个三连支持一下！谢谢大家！💖💝❣️

http://www.lryc.cn/news/228.html

相关文章：

  • canvas 制作2048
  • playwright: 全局修改页面等待超时时间
  • C++类和对象（中）
  • Docker安装EalasticSearch、Kibana，安装Elasticvue插件
  • 算法训练营 day39 贪心算法 无重叠区间 划分字母区间 合并区间
  • c/c++开发，无可避免的文件访问开发案例
  • MySQL学习笔记
  • ccs导入工程失败的处理方法
  • 探针台常见的故障及解决方法
  • 域内资源探测
  • c# 将数据导出到EXCEL文件
  • 微服务 分片 运维管理
  • 批量占满TEMP表空间问题处理与排查
  • Pytorch中的tensor和variable
  • 暗月内网渗透实战——项目七
  • 【Java 面试合集】描述下Objec类中常用的方法（未完待续中...）
  • SQLSERVER 的 truncate 和 delete 有区别吗？
  • 【C++】CC++内存管理
  • 数据预处理之图像去空白
  • 真的麻了，别再为难软件测试员了......
  • 2月9日,30秒知全网,精选7个热点
  • 球面坐标系下的三重积分
  • 谷歌 Jason Wei | AI 研究的 4 项基本技能
  • excel数据整理：合并计算快速查看人员变动
  • vit-pytorch实现 MobileViT注意力可视化
  • Python将字典转换为csv
  • EasyX精准帧率控制打气球小游戏
  • 你知道 GO 中什么情况会变量逃逸吗？
  • 一篇文章学懂C++和指针与链表
  • TPGS-cisplatin顺铂修饰维生素E聚乙二醇1000琥珀酸酯