动态规划-背包问题
文章目录
- 一、背包问题
- 1. 背包问题简介
- 2. 背包问题解决方法
- 二、01 背包问题
- 1. 实现思路
- 2. 实现代码
- 三、完全背包问题
- 1. 实现思路
- 2. 实现代码
- 四、多重背包问题(一)
- 1. 实现思路
- 2. 实现代码
- 五、多重背包问题(二)
- 1. 实现思路
- 2. 实现代码
- 六、分组背包问题
- 1. 实现思路
- 2. 实现代码
一、背包问题
1. 背包问题简介
- 背包问题可以理解为,给定一个背包容量 target,再给定一个数组 nums(用以表示物品),能否按一定方式选取 nums 中的元素得到 target。
- 这里需要注意的有以下几点:
- (1) 背包容量 target 和物品 nums 的类型可能是数,也可能是字符串。
- (2) target 可能题目已经给出(显式),也可能是需要我们从题目的信息中挖掘出来(非显式)(常见的非显式 target 比如 sum/2 等)。
- (3) 选取方式有常见的一下几种:每个元素选一次/每个元素选多次/选元素进行排列组合 那么对应的背包问题就是下面我们要讲的背包分类。
- 背包问题主要可以分为四类,分别是:01 背包问题,完全背包问题,多重背包问题和分组背包问题。
- (1) 01 背包问题
- 01 背包问题是一种非常经典的背包问题。
- 01 背包问题主要是给定一个背包容量 VVV,再给定 NNN 件物品,每个物品有两种属性,分别是体积 viv_ivi 和价值(权重) wiw_iwi,每件物品最多可以使用一次(即不是 0 次就是 1 次两种选择)。
- 问题是要在背包能装下的情况下,所挑出的物品总价值最大。
- (2) 完全背包问题
- 完全背包问题每件物品有无限个,只要背包的体积够用,就可以无限装同一个物品。
- (3) 多重背包问题
- 每个物品最多有 sis_isi 个,包含一个朴素版和优化版。
- (4) 分组背包问题
- 有 NNN 组物品,每一组物品有若干个,每组物品当中只可以选一个,在此限制条件下求物品的最大价值。
- 上述的四种问题都是在背包体积足够的情况下,求解所能容纳物品的最大价值,这里需要注意的是,背包不一定非要装满。
2. 背包问题解决方法
- 对于上述问题,我们常使用动态规划解决此类问题。
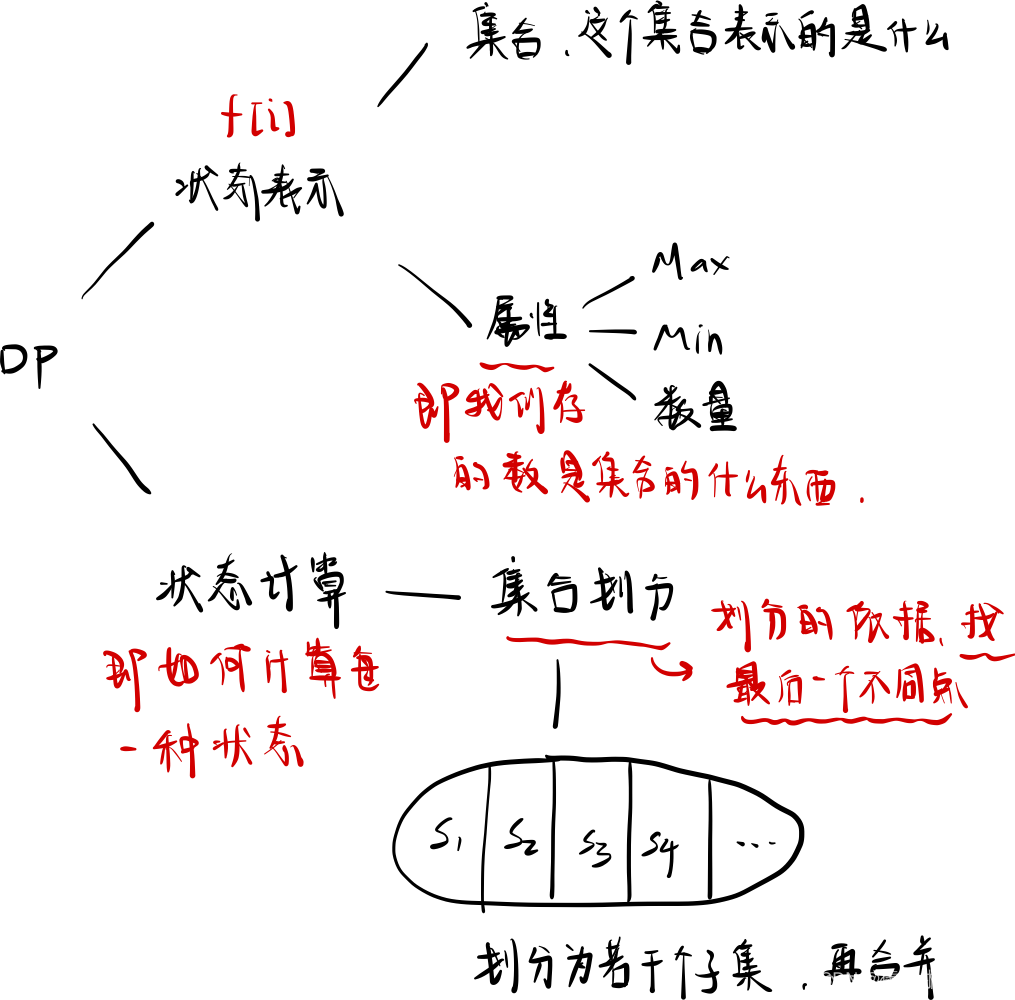
- 动态规划总共包括两大部分,分别是状态表示(判断是几维,两维就是 f(i,j)f(i,j)f(i,j),每一个状态的含义是什么)和状态计算(如何计算出每一个 f(i,j)f(i,j)f(i,j))。
- 动态规划的优化通常都是对代码或者计算方程进行等价变化。
- f(i,j)f(i,j)f(i,j) 表示的选择方法只指从前 iii 个物品中选和总体积不超过 jjj。
- 状态表示可分为集合(每一个状态表示的都是一个集合)和属性(包括最大值,最小值,元素的数量,我们的背包问题就是属性当中的最大值)。
- 状态计算对应的是集合的划分(每一个元素当前只会属于一个集合,每一个元素都存在),将 f(i,j)f(i,j)f(i,j) 划分为若干个子集和,每一个子集合都可以由更小的子集合表示。
二、01 背包问题
题目描述
有 NNN 件物品和一个容量是 VVV 的背包。每件物品只能使用一次。
第 iii 件物品的体积是 viv_ivi,价值是 wiw_iwi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,NNN,VVV,用空格隔开,分别表示物品数量和背包容积。
接下来有 NNN 行,每行两个整数 vi,wiv_i,w_ivi,wi,用空格隔开,分别表示第 iii 件物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤10000<N,V≤10000<N,V≤1000
0<vi,wi≤10000<v_i,w_i≤10000<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例
8
具体实现
1. 实现思路
- 01 背包问题的集合划分是一种非常经典的划分方法,可整体划分为两部分,不包含 iii 和包含 iii。
- 不包含 iii 可以理解为,从 1到i−11到i-11到i−1 当中选取物品,总体积不大于 jjj,该集合的最大值就是 f(i−1,j)f(i-1,j)f(i−1,j)。
- 包含 iii 可以理解为,从 1到i1到i1到i 当中选取物品,总体积不大于 jjj,该集合的最大值直接求取的困难很大,我们可以曲线救国,先将所有选法当中的第 iii 个物品去掉(最大的那部分是依旧是最大的),便转换为从 1到i−11到i-11到i−1 当中选取物品,总体积不大于 j−vij-v_ij−vi,此时所有选法的最大值就是 f(i−1,j−vi)f(i-1,j-v_i)f(i−1,j−vi),但由于我们去掉过第 iii 个物品,因此,原本的最大值就是 f(i−1,j−vi)+wif(i-1,j-v_i)+w_if(i−1,j−vi)+wi。
- 那么,最后所有的最大值就是 max(f(i−1,j),f(i−1,j−vi)+wi)max(f(i-1,j),f(i-1,j-v_i)+w_i)max(f(i−1,j),f(i−1,j−vi)+wi)。
- 上述采用的是二维实现方法,对此,可以使用滚动数组将二维降阶为一维。
2. 实现代码
#include <bits/stdc++.h>using namespace std;const int N = 1010;//n, m表示物品种数和背包体积
int n, m;
//v[N], w[N]表示物品的体积和价值
int v[N], w[N];
//f[N][N]表示总价值
int f[N][N];int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ){cin >> v[i] >> w[i];}//二维实现方法for (int i = 1; i <= n; i ++ ){for (int j = 0; j <= m; j ++ ){f[i][j] = f[i - 1][j];if (j >= v[i]) //如果可以装下当前第i个物品{f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);}}} cout << f[n][m] << endl;return 0;
}
三、完全背包问题
题目描述
有 NNN 种物品和一个容量是 VVV 的背包,每种物品都有无限件可用。
第 iii 种物品的体积是 viv_ivi,价值是 wiw_iwi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行两个整数,NNN,VVV,用空格隔开,分别表示物品种数和背包容积。
接下来有 NNN 行,每行两个整数 vi,wiv_i,w_ivi,wi,用空格隔开,分别表示第 iii 种物品的体积和价值。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤10000<N,V≤10000<N,V≤1000
0<vi,wi≤10000<v_i,w_i≤10000<vi,wi≤1000
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例
10
具体实现
1. 实现思路
- 完全背包问题和 01 背包问题的区别在于完全背包问题当中的物品可以被选择无数次。
- 完全背包问题可以选择使用一维或二维进行解决,如果直接使用与 01 背包问题相同的方法是三个 for 循环,此时会超时,就需要进行优化。
- 那么,f[i]f[i]f[i] 就表示体积是 iii 的情况下,最大价值是多少(状态表示)。
- f[0……m]f[0……m]f[0……m] 当中的最大值就是我们所求的结果。
2. 实现代码
#include <bits/stdc++.h>using namespace std;const int N = 1010;//n, m表示物品数量和背包体积
int n, m;
//v[N], w[N]表示物品的体积和价值
int v[N], w[N];
//f[N]表示总价值
int f[N];int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ){cin >> v[i] >> w[i];}for (int i = 1; i <= n; i ++ ){for (int j = v[i]; j <= m; j ++ ){f[j] = max(f[j], f[j - v[i]] + w[i]);}}cout << f[m] << endl;return 0;
}
四、多重背包问题(一)
题目描述
有 NNN 种物品和一个容量是 VVV 的背包。
第 iii 种物品最多有 sis_isi 件,每件体积是 viv_ivi,价值是 wiw_iwi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,NNN,VVV,用空格隔开,分别表示物品种数和背包容积。
接下来有 NNN 行,每行三个整数 vi,wi,siv_i,w_i,s_ivi,wi,si,用空格隔开,分别表示第 iii 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000<N,V≤1000<N,V≤100
0<vi,wi,si≤1000<v_{i},w_{i},s_{i}≤1000<vi,wi,si≤100
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例
10
具体实现
1. 实现思路
- 多重背包问题与上述两种背包问题的区别在于每个物品最多有 sis_isi 个。
- 此题与 01 背包问题基本相同。
2. 实现代码
#include <bits/stdc++.h>using namespace std;const int N = 110;//n, m表示物品种数和背包体积
int n, m;
//v[N], w[N],s[N]表示物品的体积,价值,数量
int v[N], w[N], s[N];
//f[N][N]表示价值
int f[N][N];int main()
{cin >> n >> m;for (int i = 1; i <= n; i ++ ){cin >> v[i] >> w[i] >> s[i];}for (int i = 1; i <= n; i ++ ){for (int j = 0; j <= m; j ++ ){for (int k = 0; k <= s[i] && k * v[i] <= j; k ++ ){f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);}}}cout << f[n][m] << endl;return 0;
}
五、多重背包问题(二)
题目描述
有 NNN 种物品和一个容量是 VVV 的背包。
第 iii 种物品最多有 sis_isi 件,每件体积是 viv_ivi,价值是 wiw_iwi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
输入格式
第一行两个整数,NNN,VVV,用空格隔开,分别表示物品种数和背包容积。
接下来有 NNN 行,每行三个整数 vi,wi,siv_i,w_i,s_ivi,wi,si,用空格隔开,分别表示第 iii 种物品的体积、价值和数量。
输出格式
输出一个整数,表示最大价值。
数据范围
0<N≤10000<N≤10000<N≤1000
0<V≤20000<V≤20000<V≤2000
0<vi,wi,si≤20000<v_{i},w_{i},s_{i}≤20000<vi,wi,si≤2000
输入样例
4 5
1 2 3
2 4 1
3 4 3
4 5 2
输出样例
10
具体实现
1. 实现思路
- 多重背包问题(二)与多重背包问题(一)的区别在于(二)的数据范围进行了扩大,如果直接暴力做法会导致超时,因此,需要进行优化。
- 由于(一)当中的做法与 01 背包问题基本相同,所以,我们只需要对与 01 背包问题相同的那一段进行优化。
- 这里引入二进制优化方法(用二进制表示十进制)。
- 举例说明,如果我们要从 0 枚举到 1023,十进制的做法需要我们枚举 1023 次,如果采用二进制做法,我们需要将 1023 分成十组,分别是 1,2,4,8,16,32,64,128,256 和 512,我们在这十组数字当中,每组任意取出一个数字,组合起来就可以得到 0 到1023 当中的任何数字,此时,我们只需要枚举 10 次即可。
2. 实现代码
#include <bits/stdc++.h>using namespace std;const int N = 12010, M = 2010;//n,m表示物品种数和背包容积
int n, m;
//v[N], w[N]表示每组物品的总体积和总价值
int v[N], w[N];
//f[M]表示价值
int f[M];int main()
{cin >> n >> m;//二进制枚举int cnt = 0;//将物品重新分组后的顺序for (int i = 1; i <= n; i ++ ){//a, b, s表示是每种物品的体积、价值和数量。int a, b, s;cin >> a >> b >> s;int k = 1; //二进制拆分,打包时每组中有 k 个同种物品while (k <= s) //最后一组的物品个数 < 2^(n+1) 1 2 4 8 16 ... 2^n 2^(n+1){cnt ++ ;v[cnt] = a * k;// 每组的体积w[cnt] = b * k;// 每组的价值s -= k; //得到剩余的物品数量k *= 2;// 注意是 k * 2,每次增长一倍,不是k * k}if (s > 0)// 二进制拆分完之后 剩下的物品个数分为新的一组{cnt ++ ;v[cnt] = a * s;w[cnt] = b * s;}}n = cnt; //将所得组数赋值给物品种数for (int i = 1; i <= n; i ++ ){for (int j = m; j >= v[i]; j -- ){f[j] = max(f[j], f[j - v[i]] + w[i]);}}cout << f[m] << endl;return 0;
}
六、分组背包问题
题目描述
有 NNN 组物品和一个容量是 VVV 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 vijv_{ij}vij,价值是 wijw_{ij}wij,其中 iii 是组号,jjj 是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式
第一行有两个整数 NNN,VVV,用空格隔开,分别表示物品组数和背包容量。
接下来有 NNN 组数据:
- 每组数据第一行有一个整数 SiS_iSi,表示第 iii 个物品组的物品数量;
- 每组数据接下来有 SiS_iSi 行,每行有两个整数 vij,wijv_{ij},w_{ij}vij,wij,用空格隔开,分别表示第 iii 个物品组的第 jjj 个物品的体积和价值;
输出格式
输出一个整数,表示最大价值。
数据范围
0<N,V≤1000<N,V≤1000<N,V≤100
0<Si≤1000<Si≤1000<Si≤100
0<vij,wij≤1000<v_{ij},w_{ij}≤1000<vij,wij≤100
输入样例
3 5
2
1 2
2 4
1
3 4
1
4 5
输出样例
8
具体实现
1. 实现思路
- 分组背包问题是指我们有 NNN 组物品,每组物品当中有若干个物品,每个物品的体积和价值各有不同,每组物品当中最多只能选一个(可以不选)。
2. 实现代码
#include <bits/stdc++.h>using namespace std;const int N = 110;//n,m表示物品组数和背包容积
int n, m;
//v[N][N], w[N][N], s[N]表示物品的体积,价值和数量
int v[N][N], w[N][N], s[N];
//f[N]表示总价值
int f[N];int main()
{cin >> n >> m;//每组物品的数据进行读入for (int i = 1; i <= n; i ++ ){cin >> s[i];for (int j = 1; j < s[i]; j ++ ){cin >> v[i][j] >> w[i][j];}}for (int i = 1; i <= n; i ++ ){for (int j = m; j >= 0; j -- ){for (int k = 0; k < s[i]; k ++ ){if (v[i][k] <= j){f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);}}}}cout << f[m] << endl;return 0;
}
