动态规划背包问题
背包问题的分类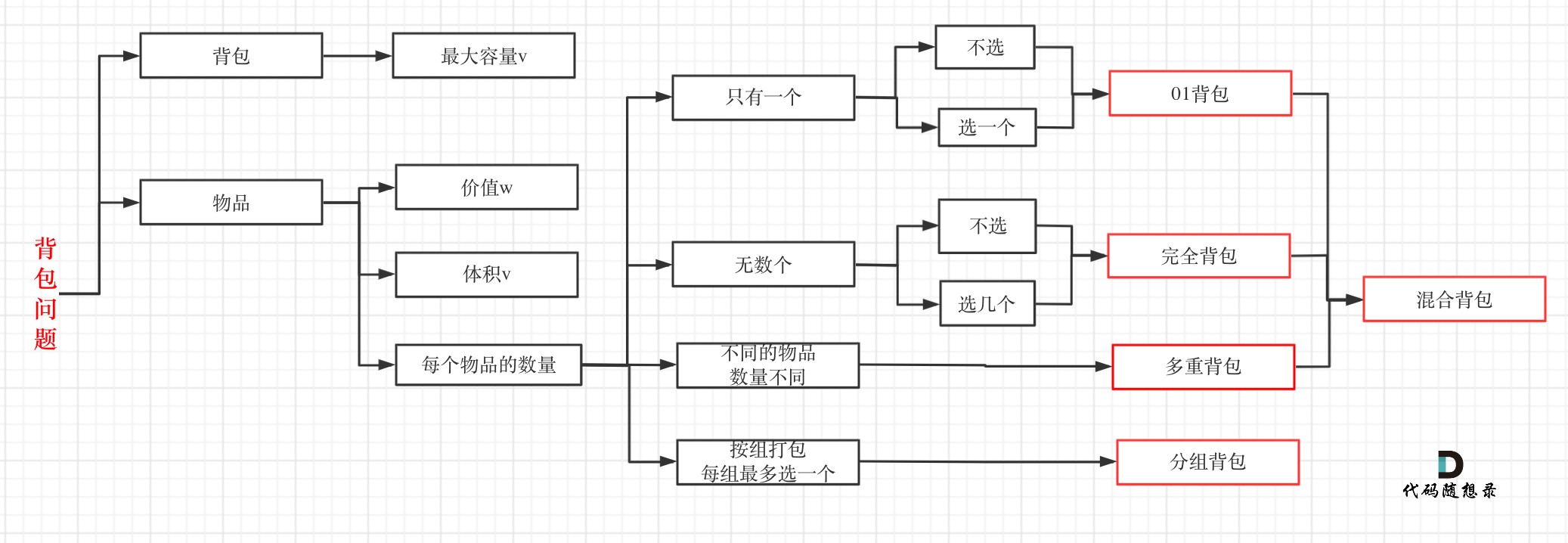
拿到背包问题,最重要的是会归类到哪一种背包问题中,常见的考题里主要是01背包和完全背包,leetcode上连多重背包的题目都没有。实际完全背包问题就是01背包的一种。
对一和零这道题,很多人容易把m看成一个背包,n看成另一个背包,从而当做多重背包。然而这不对,背包有两个维度,一个是m 一个是n,而不同长度的字符串就是不同大小的待装物品。
dp[i][j] 可以由前一个strs里的字符串推导出来,strs里的字符串有zeroNum个0,oneNum个1。
dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。所以递推公式:dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);对0-1背包,常用二维dp数组:dp[i][j]表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少
背包问题会怎么提问
- 问能否能装满背包(或者最多装多少):dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ,对应题目如下:
