796. 子矩阵的和（二维前缀和）

题目：

796. 子矩阵的和 - AcWing题库

思路： 

1.暴力搜索（搜索时间复杂度为O(n2)，很多时候会超时）

2. 前缀和（左上角（二维）前缀和）：本题特殊在不是直接求前n个数的和，而是求矩阵中某个元素左上角所以数的和（包括该元素自己），利用左上角前缀和的运算求子矩阵和。

3.在求左上角前缀和以及由左上角前缀和求子矩阵的过程中都需要运用到容斥原理！！！

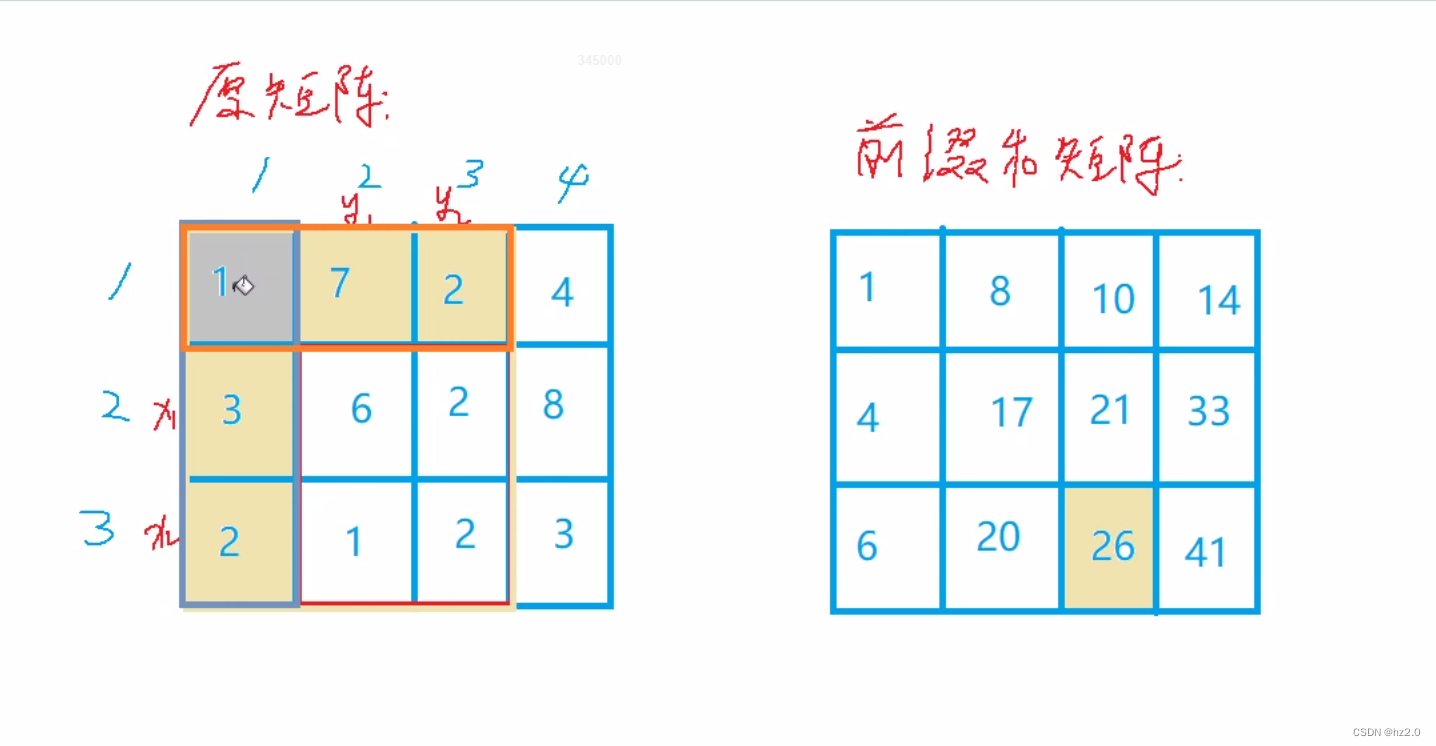
代码：

#include<iostream>
#include<cstdio>
using namespace std;
typedef unsigned long long ull;
const int N = 1010;
int n, m, q;
ull a[N][N], s[N][N];//a存储数据，s存储左上前缀和
int main()
{cin >> n >> m >> q;for (int i = 1; i <= n; i++)//入读数据for (int j = 1; j <= m; j++)scanf("%d", &a[i][j]);for (int i = 1; i <= n; i++)//求左上前缀和for (int j = 1; j <= m; j++)s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];//容斥原理while (q--) {ull x1, y1, x2, y2;scanf("%llu%llu%llu%llu", &x1, &y1, &x2, &y2);printf("%lld\n", s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]);//容斥原理}
}