当前位置：首页 > news >正文

数据结构与算法之打家劫舍(一)动态规划思想

news 2025/8/9 12:32:12

动态规划里面一部题目打家劫舍是一类经典的算法题目之一，他有各种各样的变式，这一篇文章和大家分享一下打家劫舍最基础的一道题目，掌握这一道题目，为下一道题目打下基础。我们直接进入正题。

一.题目

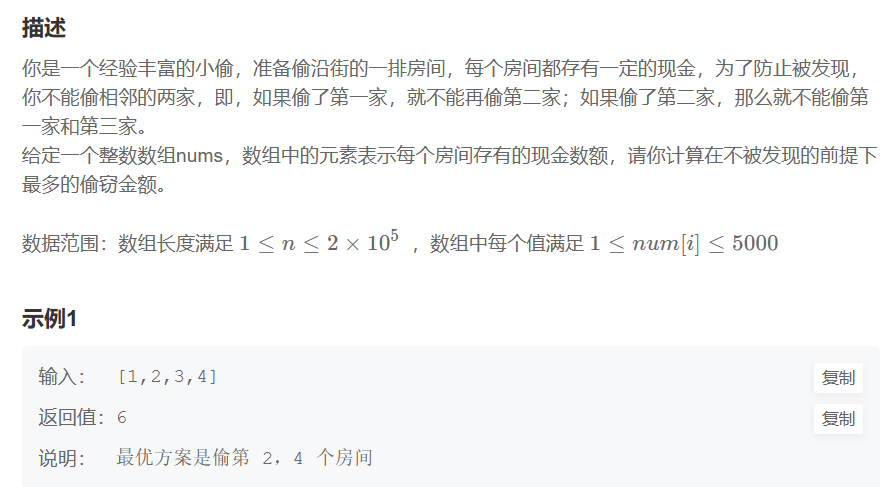
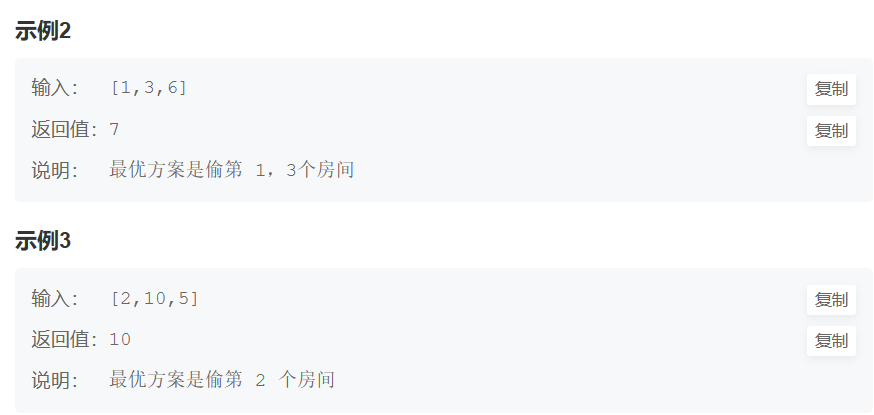
大家如果刚接触这样的题目，会有点困惑，当前的状态我是偷还是不偷呢？

仔细一想，当前房屋偷与不偷取决于前一个房屋和前两个房屋是否被偷了。

所以这里就更感觉到，当前状态和前面状态会有一种依赖关系，那么这种依赖关系都是动规的递推公式。

当然以上是大概思路，打家劫舍是dp解决的经典问题，接下来我们来动规五部曲分析如下：

二.动态规划五部曲

确定dp数组（dp table）以及下标的含义

dp[i]：考虑下标i（包括i）以内的房屋，最多可以偷窃的金额为dp[i]。

2.确定递推公式

决定dp[i]的因素就是第i房间偷还是不偷。

如果偷第i房间，那么dp[i] = dp[i - 2] + nums[i] ，即：第i-1房一定是不考虑的，找出下标i-2（包括i-2）以内的房屋，最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。

如果不偷第i房间，那么dp[i] = dp[i - 1]，即考虑i-1房，（注意这里是考虑，并不是一定要偷i-1房，这是很多人容易混淆的点）

然后dp[i]取最大值，即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);

3.dp数组如何初始化

从递推公式dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);可以看出，递推公式的基础就是dp[0] 和 dp[1]

从dp[i]的定义上来讲，dp[0] 一定是 nums[0]，dp[1]就是nums[0]和nums[1]的最大值即：dp[1] = max(nums[0], nums[1]);

代码如下：

vector<int> dp(nums.size());
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);

4.确定遍历顺序

dp[i] 是根据dp[i - 2] 和 dp[i - 1] 推导出来的，那么一定是从前到后遍历！

代码如下：

for (int i = 2; i < nums.size(); i++) {dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}

5.举例推导dp数组

以示例二，输入[2,7,9,3,1]为例。

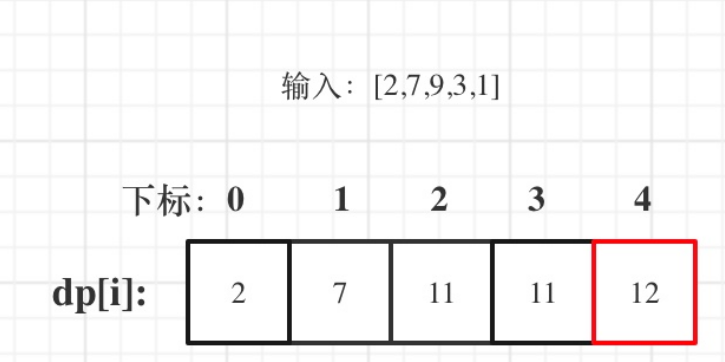
红框dp[nums.size() - 1]为结果。

以上分析完毕，C++代码如下：

class Solution {
public:int rob(vector<int>& nums) {if (nums.size() == 0) return 0;if (nums.size() == 1) return nums[0];vector<int> dp(nums.size());dp[0] = nums[0];dp[1] = max(nums[0], nums[1]);for (int i = 2; i < nums.size(); i++) {dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);}return dp[nums.size() - 1];}
};

Java代码如下：

// 动态规划
class Solution {public int rob(int[] nums) {if (nums == null || nums.length == 0) return 0;if (nums.length == 1) return nums[0];int[] dp = new int[nums.length];dp[0] = nums[0];dp[1] = Math.max(dp[0], nums[1]);for (int i = 2; i < nums.length; i++) {dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);}return dp[nums.length - 1];}
}