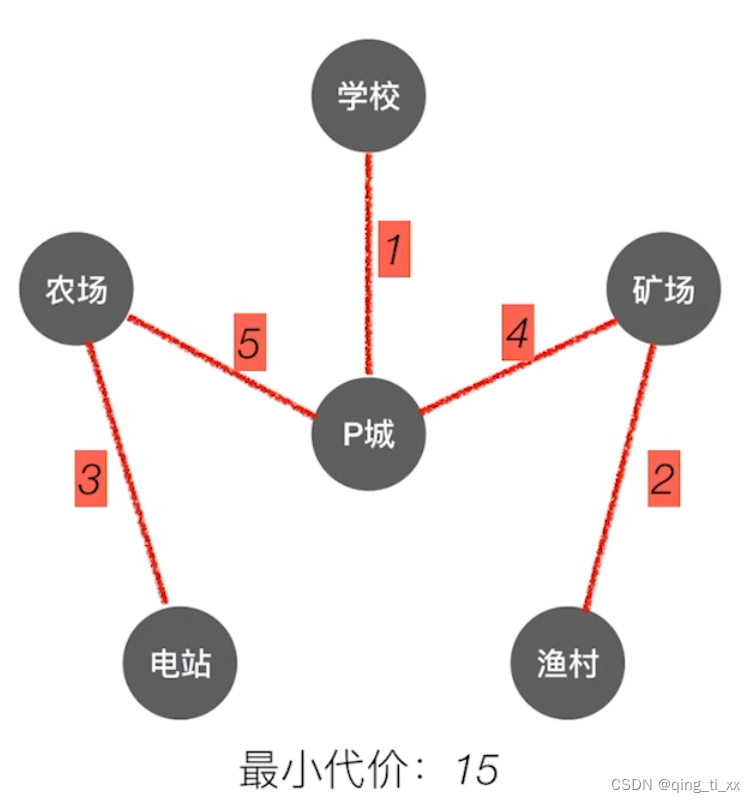
第六章 图 六、最小生成树(Prim算法、Kruskal算法)
一、定义
对于一个带权连通无向图G=(V,E),生成树不同,每棵树的权(即树中所有边上的权值之和)也可能不同。设R为G的所有生成树的集合,若T为R中边的权值之和最小的生成树,则T称为G的最小生成树(Minimum-Spanning-Tree, MST)。


二、手动实现算法
(1)Prim算法
介绍:从某一个顶点开始构建生成树;每次将代价最小的新顶点纳入生成树,直到所有顶点都纳入为止。
时间复杂度:O(),适合用于边稠密图
例子1:
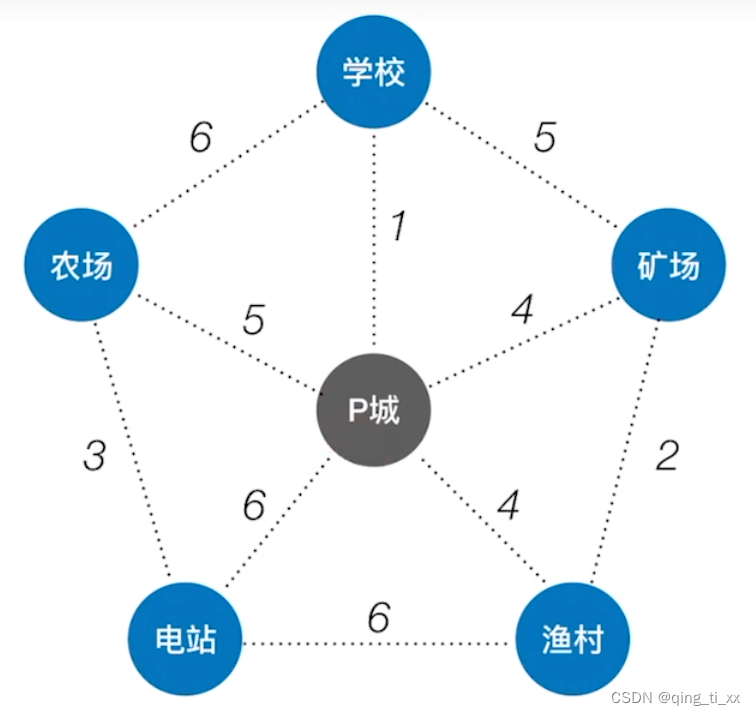
1、我们从P城开始,找到权最小的路径,并构建出新的树。此时最小为1
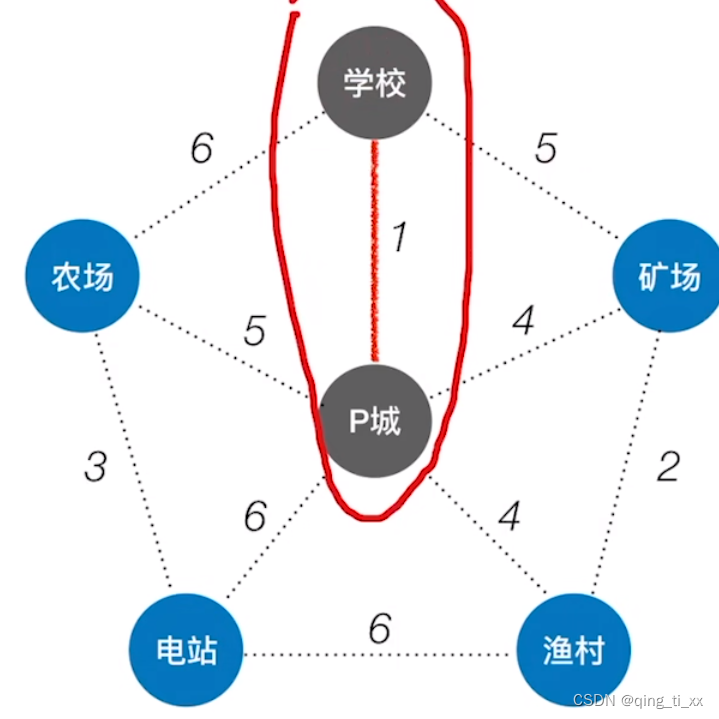
2、再次寻找权最短的路径,为P城到矿场。
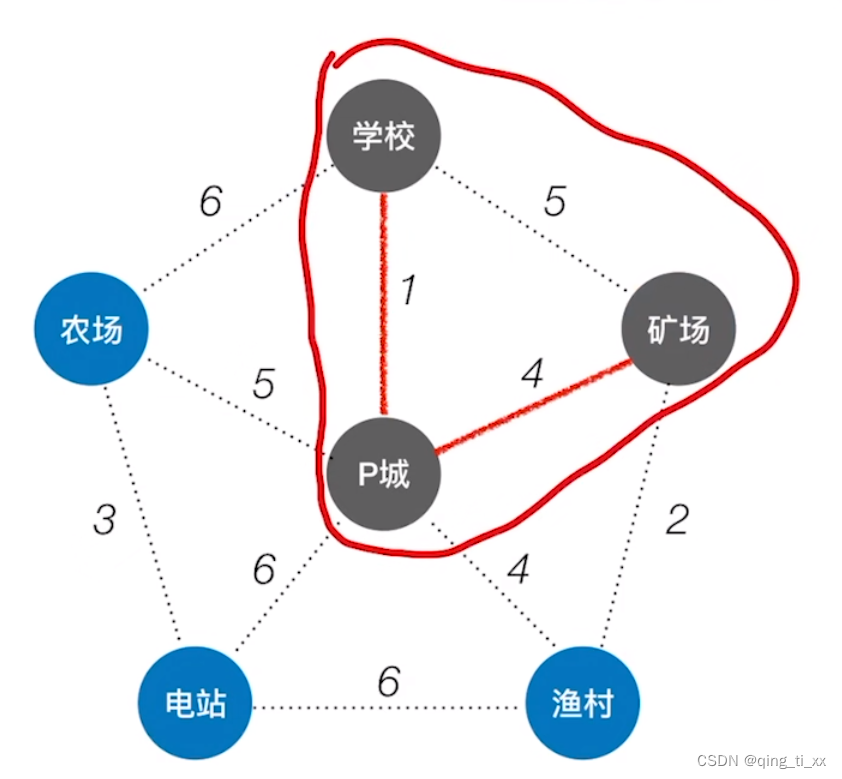
3、如此反复,得到最终结果。
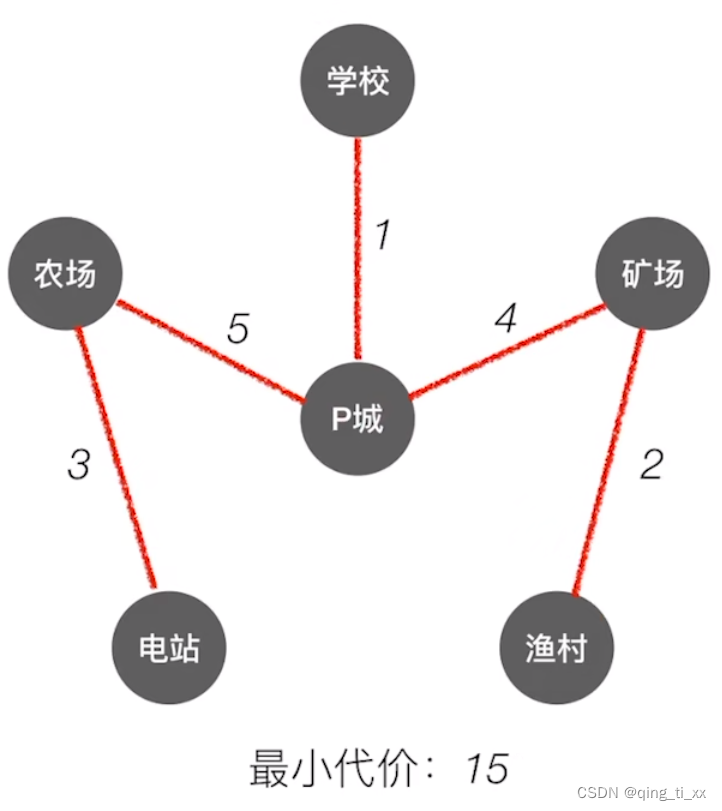
(2)Kruskal算法
介绍:每次选择一条权值最小的边,使这条边的两头连通(原本已经连通的就不选),直到所有结点都连通。
时间复杂度:O(|E|*log2|E|),适合用于边稀疏图
例子2:
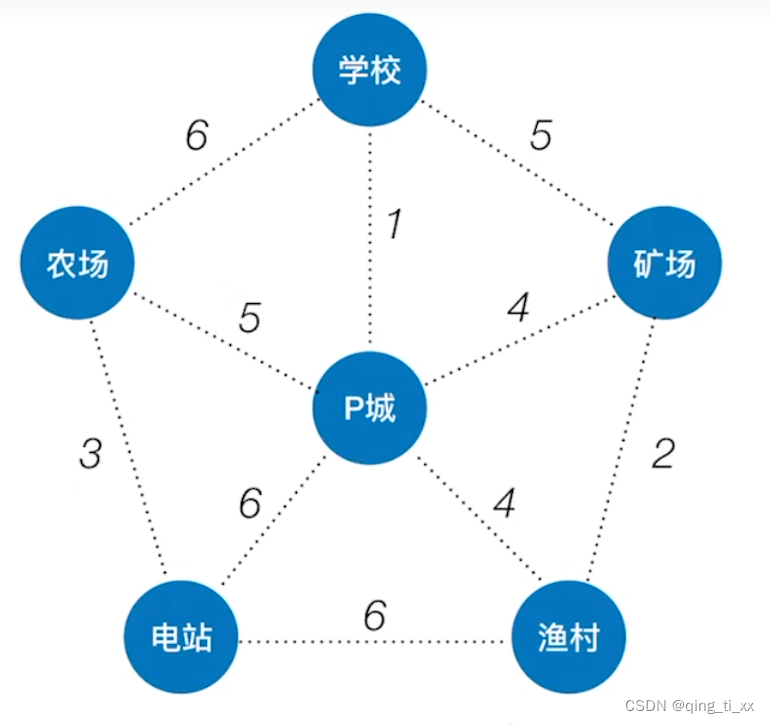
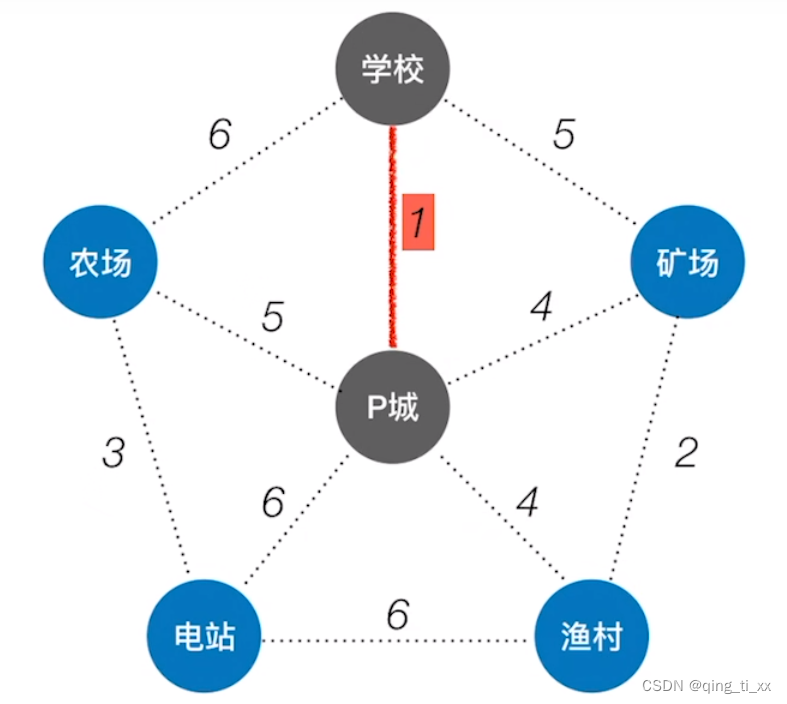
1、我们从P城出发,找一条权值最小的边,我们找到学校到P城的路径为1(最短),于是连通它们。
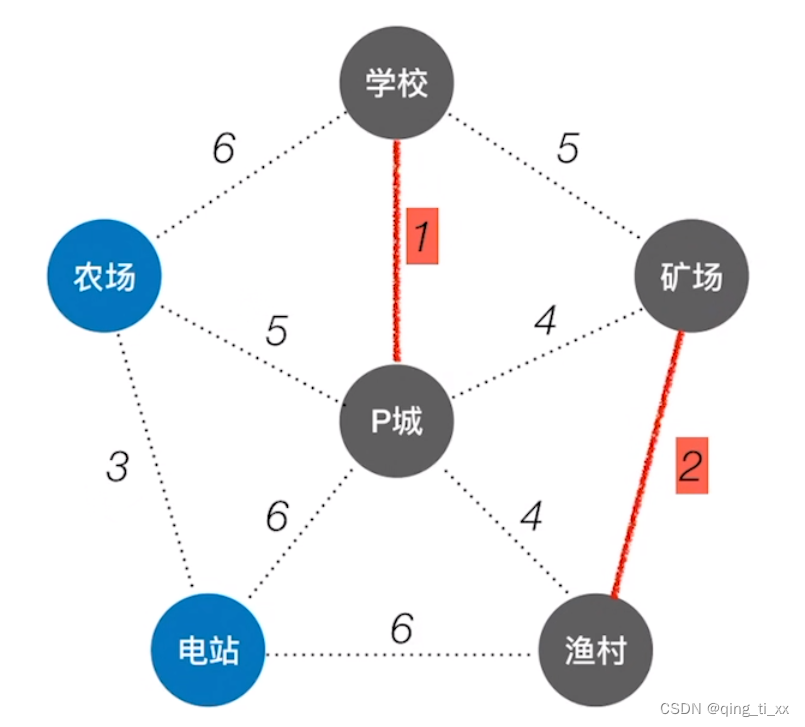
2、再次找最短,找到2,连通它们。
3、反复执行这个操作,直到所有的结点都连通。