算法 数据结构 递归插入排序 java插入排序 递归求解插入排序算法 如何用递归写插入排序 插入排序动图 插入排序优化 数据结构（十）

1. 插入排序（insertion-sort）：

                                          是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入

    算法稳定性:

                        对于两个相同的数，经过排序后，他们依旧保持之前的顺序，二者次序没有发生变化。插入排序是算法稳定的

   时间复杂度：

        最优情况

                      在插入排序中，当待排序数组是有序时，是最优的情况，只需当前数跟前一个数比较一下就可以了，这时一共需要比较N- 1次，时间复杂度为O(n)

        最坏情况

                          最坏的情况是待排序数组是逆序的，此时需要比较次数最多，总次数记为：1+2+3+…+N-1，所以，插入排序最坏情况下的时间复杂度为O() 

     动态图：

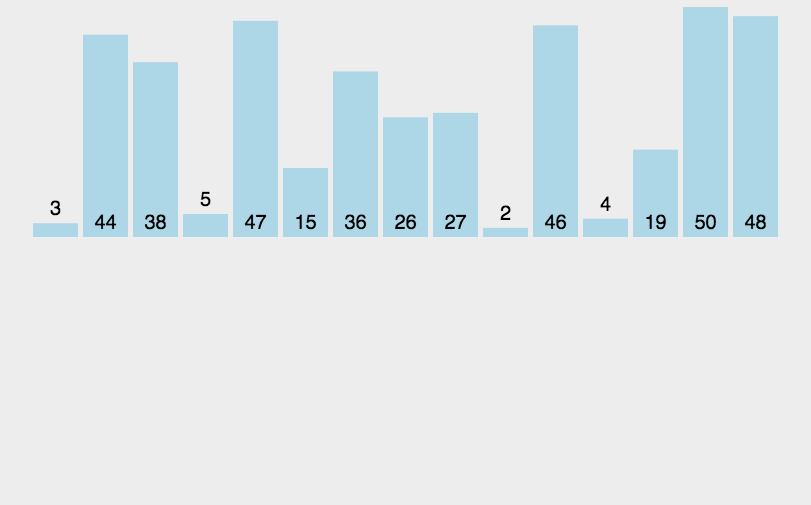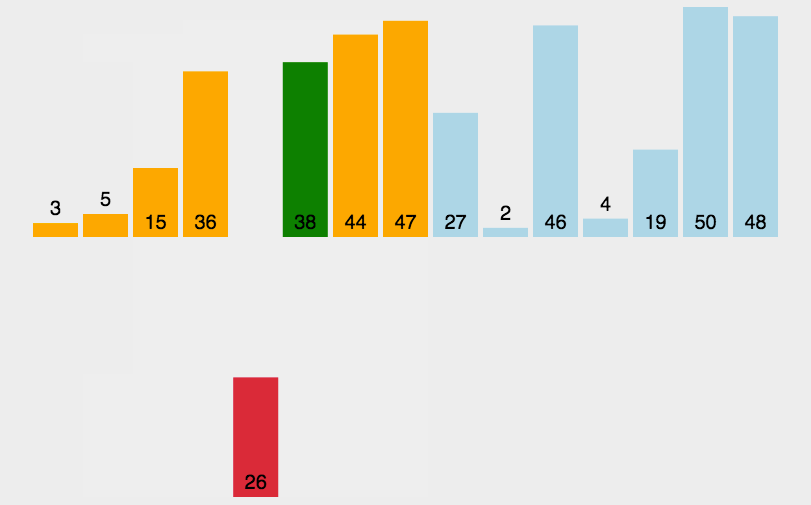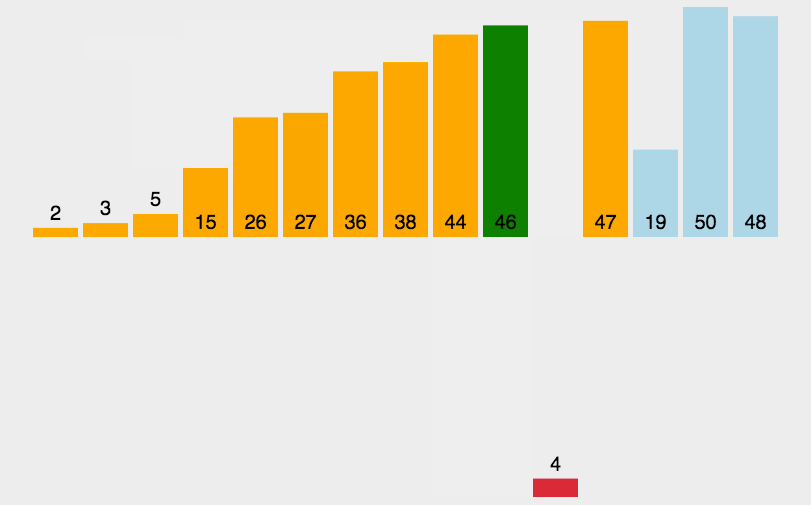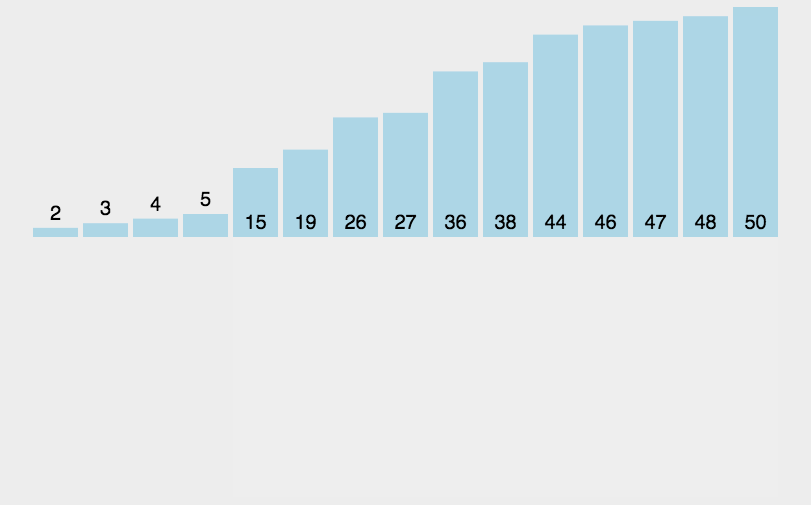
  递归代码：

package com.nami.algorithm.study.day06;import java.util.Arrays;/*** beyond u self and trust u self.** @Author: lbc* @Date: 2023-09-05 15:36* @email: 594599620@qq.com* @Description: keep coding*/
public class InsertionSort {/*** 插入排序：* 从右向左找** @param target*/public static void sort(int[] target) {insertion(target, 1);}/*** 递归 缩小结果集** @param target* @param lowIndex*/private static void insertion(int[] target, int lowIndex) {if (lowIndex == target.length) {return;}int t = target[lowIndex];// 已排序区域指针int i = lowIndex - 1;// 没有找到插入位置while (i >= 0 && target[i] > t) {target[i + 1] = target[i];i--;// 如果到达数组0时候 依旧没有找到，则退出循环// 抽出，合并到while内
//            if(i < 0) {
//                break;
//            }}//插入位置找到了// 优化减少不必要的赋值动作，// 需要替换的数组值，正好是大于i, i+1索引的值不需要动，这个赋值动作就不必要了if (i + 1 != lowIndex) {target[i + 1] = t;}insertion(target, lowIndex + 1);}/*** 两种写法，这种赋值次数更多* 时间复杂度相同* 但是 效率没有上面的高，消耗在更多的赋值操作上了** @param target* @param lowIndex*/private static void insertion0(int[] target, int lowIndex) {if (lowIndex == target.length) {return;}// 已排序区域指针int i = lowIndex - 1;// 没有找到插入位置while (i >= 0 && target[i] > target[i + 1]) {int temp = target[i];target[i] = target[i + 1];target[i + 1] = temp;i--;}insertion(target, lowIndex + 1);}public static void main(String[] args) {int[] test = new int[]{1, 54, 234, 675, 32432, 23, 78, 459, 354, 9, 344, 22, 46, 85, 236, 3278, 245, 83, 154, 2, 1, 34, 73, 23};int[] test2 = new int[]{2, 4, 7, 3, 2, 1};
//        sort(test, test.length);sort(test);System.out.println(Arrays.toString(test));}}