二叉树的递归遍历和非递归遍历
目录
一.二叉树的递归遍历
1.先序遍历二叉树
2.中序遍历二叉树
3.后序遍历二叉树
二.非递归遍历(栈)
1.先序遍历
2.中序遍历
3.后序遍历
一.二叉树的递归遍历
定义二叉树
#其中TElemType可以是int或者是char,根据要求自定
typedef struct BiNode{TElemType data;struct BiNode, *lchild,*rchild;}BiNode,*BiTree;void visit(TElemType data) {printf("%d ", data);
}1.先序遍历二叉树
void PreOrderTraverse(BiTree T)
{if(T==NULL)return ok;//空二叉树else{visit(T);//访问根节点PreOrderTraverse(T->lchild);//递归遍历左子树PreOrderTraverse(T->rchild);//递归遍历右子树}
}2.中序遍历二叉树
void InOrderTraverse(BiTree T)
{if(T==NULL)return ok;//空二叉树else{InOrderTraverse(T->lchild);//递归遍历左子树visit(T);//访问根节点InOrderTraverse(T->rchild);//递归遍历右子树}
}3.后序遍历二叉树
void PostOrderTraverse(BiTree T)
{if(T==NULL)return ok;//空二叉树else{PostOrderTraverse(T->lchild);//递归遍历左子树PostOrderTraverse(T->rchild);//递归遍历右子树visit(T);//访问根节点}
}遍历的规则,以先序遍历为例:
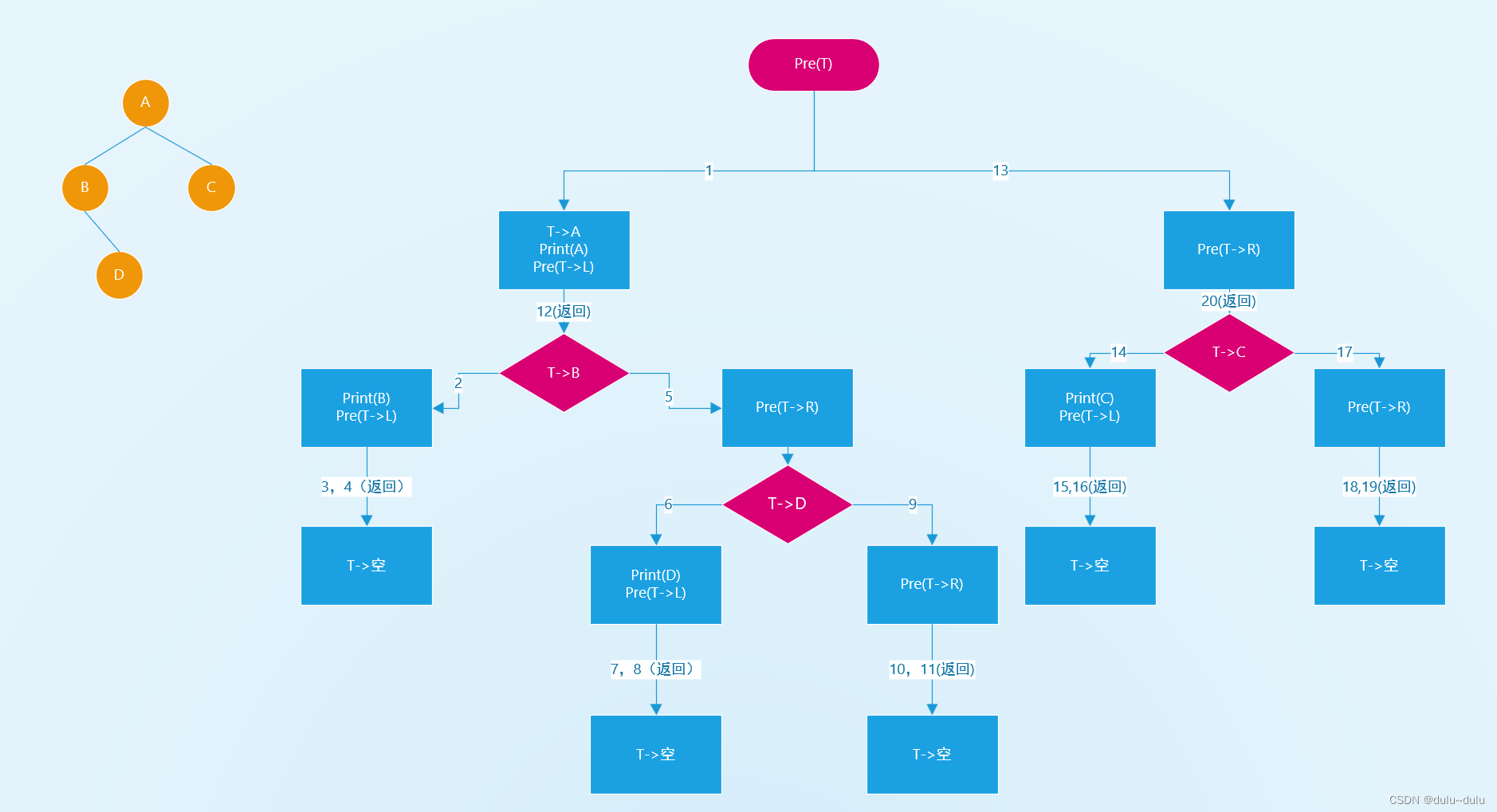
如果去掉输出语句,从递归角度,三种算法是完全相同的,三种算法访问路径是相同的,只是访问时机不同
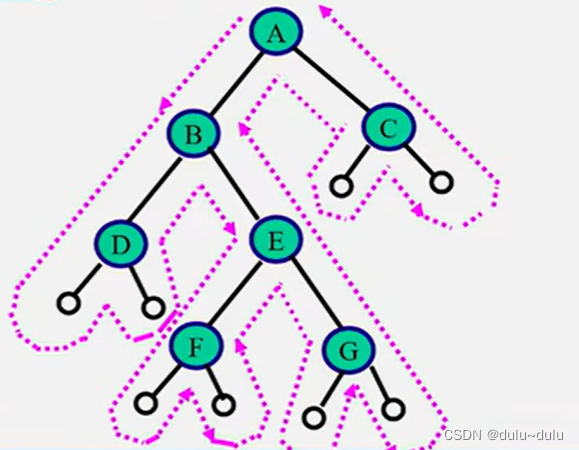
第一次经过时访问=先序遍历
第二次经过时访问=中序遍历
第三次经过时访问=后序遍历
二.非递归遍历(栈)
typedef struct BiTNode {char data;struct BiTNode *lchild, *rchild;
} BiTNode, *BiTree;typedef struct {BiTree data[MAX_SIZE];int top;
} Stack;void InitStack(Stack** S) {*S = (Stack*)malloc(sizeof(Stack));(*S)->top = -1;
}int StackEmpty(Stack* S) {return (S->top == -1);
}int StackFull(Stack* S) {return (S->top == MAX_SIZE - 1);
}void push(Stack* S, BiTree elem) {if (StackFull(S)) {printf("Stack is full. Cannot push element.\n");return;}S->top++;S->data[S->top] = elem;
}void pop(Stack* S, BiTree* elem) {if (StackEmpty(S)) {printf("Stack is empty. Cannot pop element.\n");return;}*elem = S->data[S->top];S->top--;
}int GetTop(Stack* S, BiTree* elem) {if (StackEmpty(S)) {printf("Stack is empty. Cannot get top element.\n");return 0;}*elem = S->data[S->top];return 1;
}
1.先序遍历
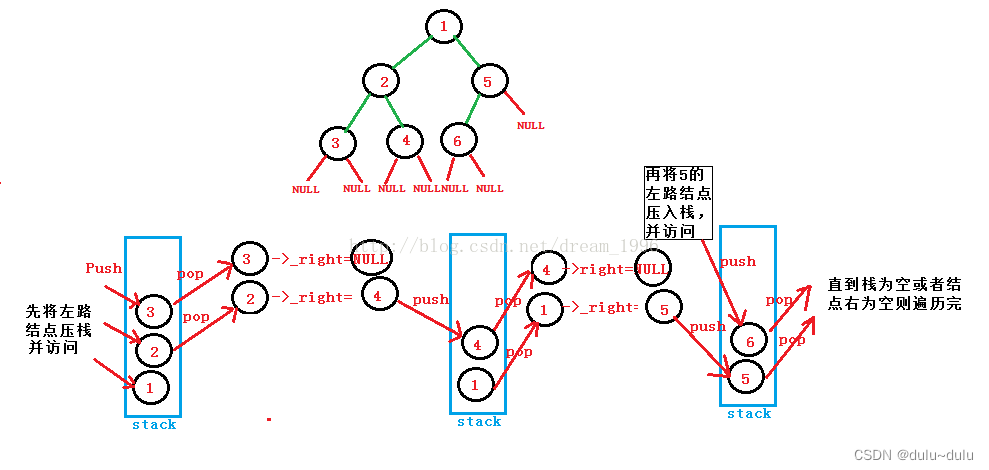
(1)从根结点开始先压左路结点,并访问结点,直到把根结点和左路结点全部压入栈。
(2)若左子树和为空,说明左路和根结点已经全部压栈并且已经访问过了,开始取栈顶元素来访问上一层父节点的右子树。把右子树看成子问题继续进行(1)
(3)依次进行上述(1)和(2)压栈访问和出栈操作,直到栈为空或者右子树为空这说明遍历完毕
void PreOrderTraverse(BiTree T)
{Stack* S;BiTree p, q;InitStack(&S);p = T;while (p || !StackEmpty(S)){if (p){printf("%c", p->data);push(S, p); // 将节点 p 入栈p = p->lchild;}else{pop(S, &q);p = q->rchild;}}free(S); // 释放 Stack 结构体内存
}
2.中序遍历
中序遍历和先序遍历思路类似,区别在于,先序遍历先访问根,在访问左,中序遍历先访问左,在访问根,最后都再访问右
void InOrderTraverse(BiTree T)
{Stack* S;BiTree p, q;InitStack(&S);p = T;while (p || !StackEmpty(S)){if (p){push(S, p);p = p->lchild;}else{pop(S, &q);printf("%c", q->data);p = q->rchild;}}free(S); // 释放 Stack 结构体内存
}
3.后序遍历
后续遍历必须访问完左右子树之后才可以访问父亲结点,所以访问完左子树时,现在得去访问右子树,通过栈找到父亲结点(这是第一次top父亲结点),然后找到父亲结点的右子树进行访问,当把右子树访问完成后,再通过栈找到父亲结点进行访问(这是第二次top父亲结点A)。那么怎么才知道这时是第一次top和第二次top呢?如果不做处理的话这里就会一直认为是第一次top父亲节点,不出栈,就会造成死循环,所以怎样解决呢?
这里创建一个prev结点,用来记录上一次出栈的结点,若上一次出栈的结点为右子树,这说明可以访问根结点了,说明是已经第二次top父亲结点
void PostOrderTraverse(BiTree T)
{Stack* S;BiTree p = T;InitStack(&S);BiTree prev = NULL;while (p || !StackEmpty(S)){while (p){push(S, p);p = p->lchild;}BiTree q;if (GetTop(S, &q) && (q->rchild == NULL || q->rchild == prev)){printf("%c ", q->data);prev = q;//更新q结点pop(S, &p);p = NULL;}else if (q->rchild != NULL){p = q->rchild;}}free(S);
}