数据结构之二叉树
🎈一.二叉树相关概念
1.树
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合,树结构通常用来存储逻辑关系为 "一对多" 的数据。例如:
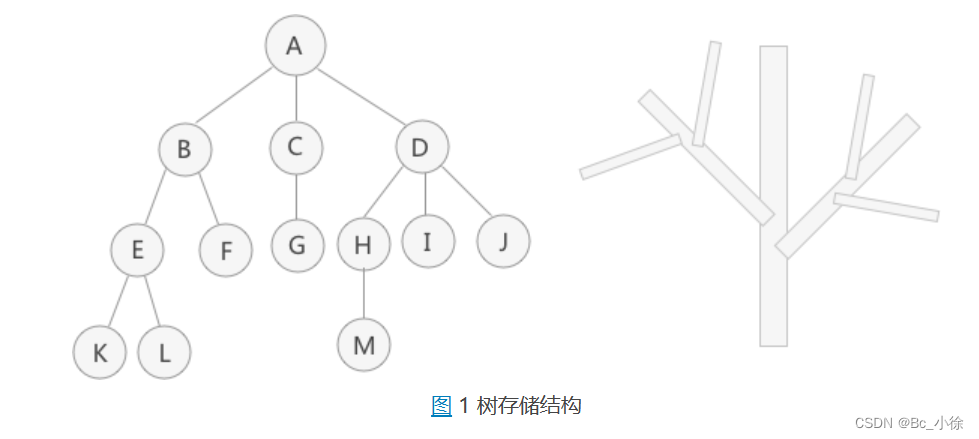
关于树的几个重要概念:
1)树的度:一棵树中,所有结点度的最大值称为树的度,如上图,这棵树的度为3;
2)节点的度:一个结点含有子树的个数称为该结点的度,如上图,A节点的度为3;
3)根节点:一棵树中,没有双亲结点的结点,如上图,A就是根节点;
4)叶子节点:简单来说,度为0的就是叶子节点,如上图,K,L,F,M等都是叶子节点;
5)树的高度或深度:树中结点的最大层次,如上图,树的高度为4;
那么什么是二叉树呢?
简单地理解,满足以下两个条件的树就是二叉树:
- 本身是有序树;
- 树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
如图:
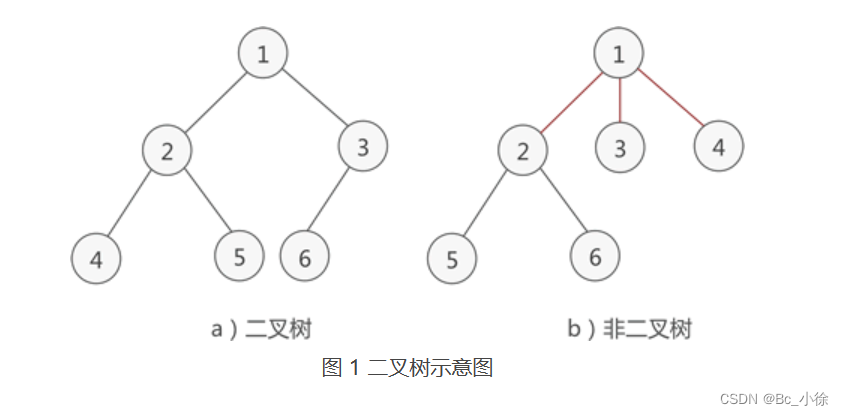
🎈二.二叉树的性质
1.若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有 2^i-1(i>0)个结点;
2.若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是2^k-1 (k>=0);
3. 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1;
✅关于此结论的推导:
对于任意一棵二叉树,一棵有N个节点的树就有N-1条边
假设度为0的节点为n0,度为1的节点为n1,度为2的节点为n2,度为0的节点没有边,度为1的节点有1条边,度为2的节点有2条边,由此可得:
N-1=n1*1+n2*2 ----------------产生的边的关系
N=n0+n1+n2 ----------------产生节点的关系
联立就可以得出这个结论:n0=n2+1
4.具有n个结点的完全二叉树的深度k为 log2(n+1)上取整;
✅习题:
1) 在具有 2n 个结点的完全二叉树中,叶子结点个数为(A);
A .n B. n+1 C. n-1 D. n/2
解析: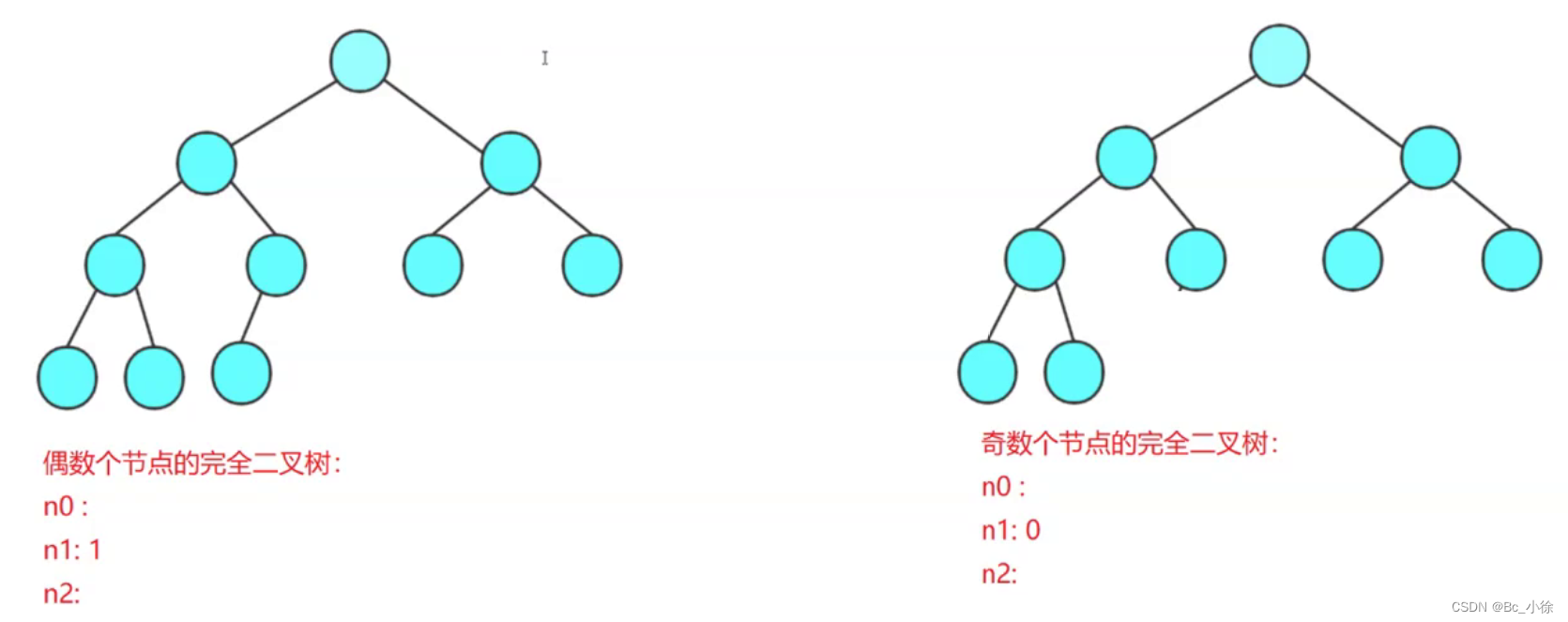
完全二叉树分奇偶数俩种情况,如上图,本题有2n个节点,是偶数,那么度为1的节点数只有1个,所以可知:
2n=n0+n1+n2;
n0=n2+1;
代入可求:n0=n;
2)一个具有767个节点的完全二叉树,其叶子节点个数为(B);
A. 383 B. 384 C. 385 D. 386
解析:因为它是一棵完全二叉树,节点数为奇数,说明它是一棵满二叉树,所以没有度为1的节点,由此可知:
767=n0+n2;
n0=n2+1;
联立上式可以求出答案
🎈三.构造二叉树
二叉树的存储结构分为:顺序存储和类似于链表的链式存储。
构造一个类,里面存放左子树,右子树,数据域;
public static class TreeNode {public char val;//数据域public TreeNode left;//左节点public TreeNode right;//右节点public TreeNode(char val) {this.val = val;}}//构造树public TreeNode createTree() {TreeNode node1 = new TreeNode('A');TreeNode node2 = new TreeNode('B');TreeNode node3 = new TreeNode('C');TreeNode node4 = new TreeNode('D');TreeNode node5 = new TreeNode('E');TreeNode node6 = new TreeNode('F');TreeNode node7 = new TreeNode('G');node1.left = node2;node1.right = node3;node2.left = node4;node2.right = node5;node3.left = node6;node3.right = node7;return node1;}
}🎈四.二叉树的相关操作
1.前序遍历
前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点--->根的左子树--->根的右子树。
//前序遍历public void preOrder(TreeNode root) {if (root == null) {return;}System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);}2.中序遍历
中序遍历(Inorder Traversal)——根的左子树--->根节点--->根的右子树。
//中序遍历public void inOrder(TreeNode root) {if (root == null) {return;}inOrder(root.left);System.out.print(root.val + " ");inOrder(root.right);}3.后序遍历
后序遍历(Postorder Traversal)——根的左子树--->根的右子树--->根节点。
//后序遍历public void postOrder(TreeNode root) {if (root == null) {return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val + " ");}4.获取书中节点的个数
// 获取树中节点的个数public int size(TreeNode root) {if (root == null) {return 0;}int leftSize = size(root.left);int rightSize = size(root.right);return leftSize + rightSize + 1;//个数=左树的节点树+右树的节点树+1}5.获取叶子节点数
// 获取叶子节点的个数public int getLeafNodeCount(TreeNode root) {if (root == null) {return 0;}if (root.left == null && root.right == null) {return 1;//如果左右两边都为空,那么一定是叶子节点}int leftSize = getLeafNodeCount(root.left);int rightSize = getLeafNodeCount(root.right);return leftSize + rightSize;}6.获取第k层的节点数
// 获取第K层节点的个数public int getKLevelNodeCount(TreeNode root, int k) {if (root == null) {return 0;}if (k == 1) {return 1;}int leftSize = getKLevelNodeCount(root.left, k - 1);int rightSize = getKLevelNodeCount(root.right, k - 1);return leftSize + rightSize;}7.获取二叉树的高度
// 获取二叉树的高度public int getHeight(TreeNode root) {if (root == null) {return 0;}int leftHeight = getHeight(root.left);int rightHeight = getHeight(root.right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}8.查找value值是否存在树中
// 检测值为value的元素是否存在public TreeNode find(TreeNode root, int val) {if (root == null) {return null;}if (val == root.val) {return root;}TreeNode leftTree = find(root.left, val);if (leftTree != null) {return leftTree;}TreeNode rightTree = find(root.right, val);if (rightTree != null) {return rightTree;}return null;}