(AcWing) 任务安排(I,II,III)
任务安排I:
有 N 个任务排成一个序列在一台机器上等待执行,它们的顺序不得改变。
机器会把这 N 个任务分成若干批,每一批包含连续的若干个任务。
从时刻 0 开始,任务被分批加工,执行第 i 个任务所需的时间是 Ti。
另外,在每批任务开始前,机器需要 S 的启动时间,故执行一批任务所需的时间是启动时间 S 加上每个任务所需时间之和。
一个任务执行后,将在机器中稍作等待,直至该批任务全部执行完毕。
也就是说,同一批任务将在同一时刻完成。
每个任务的费用是它的完成时刻乘以一个费用系数 Ci。
请为机器规划一个分组方案,使得总费用最小。
输入格式
第一行包含整数 N。
第二行包含整数 S。
接下来 N 行每行有一对整数,分别为 Ti 和 Ci,表示第 i 个任务单独完成所需的时间 Ti 及其费用系数 Ci。
输出格式
输出一个整数,表示最小总费用。
数据范围
1≤N≤5000,
0≤S≤50,
1≤Ti,Ci≤100
输入样例:
5
1
1 3
3 2
4 3
2 3
1 4
输出样例:
153#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
const int N = 5010;
ll sumt[N],sumc[N],f[N];
//sumt[N]时间前缀和
//sumc[N]费用前缀和
//f[N]是将前i个任务处理完的所有方案的集合
ll n,s;int main()
{cin>>n>>s;for(int i=1;i<=n;i++){int t,c;cin>>t>>c;sumt[i] = t + sumt[i-1];sumc[i] = c + sumc[i-1];}memset(f,0x3f,sizeof f);//预防下面求最小值出错,先初始化为无穷大f[0] = 0;//前0个任务处理完的方案数自然为0for(int i=1;i<=n;i++){for(int j=0;j<i;j++){f[i] = min(f[i],f[j]+sumt[i]*(sumc[i]-sumc[j])+s*(sumc[n]-sumc[j]));}}cout<<f[n]<<endl;return 0;
} 
AcWing 300. 任务安排1【线性DP+费用提前计算思想】 - AcWing
任务安排II:斜率优化DP
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;typedef long long ll;
const int N = 300010;
int n,s;
ll c[N],t[N],f[N],q[N];int main()
{cin>>n>>s;//读入数据计算时间和代价的前缀和for(int i=1;i<=n;i++){int a,b;cin>>a>>b;c[i] = c[i-1]+b;t[i] = t[i-1]+a;}int hh=0,tt=0; //hh是队头,tt的队尾q[0] = 0; //数组q表示的是队列,队列一开始存在(0,0)点for(int i=1;i<=n;i++){//将小于等于目标斜率的点全部删掉 (删除的是组成斜率的两个点中的第一个点)while(hh<tt&&(f[q[hh+1]]-f[q[hh]])<=(t[i]+s)*(c[q[hh+1]]-c[q[hh]])) hh++;//对头的元素就是我们所求的f[i]最小的点int j = q[hh];//代入公式f[i] = f[j] - (t[i]+s)*c[j]+t[i]*c[i] + s*c[n];//计算完后插入新的点,插入前应该将队尾所有不在凸包上的点均删掉while(hh<tt&&(f[q[tt]]-f[q[tt-1]])*(c[i]-c[q[tt]])>=(f[i]-f[q[tt]])*(c[q[tt]]-c[q[tt-1]])) tt--;q[++tt] = i;}cout<<f[n]<<endl;
}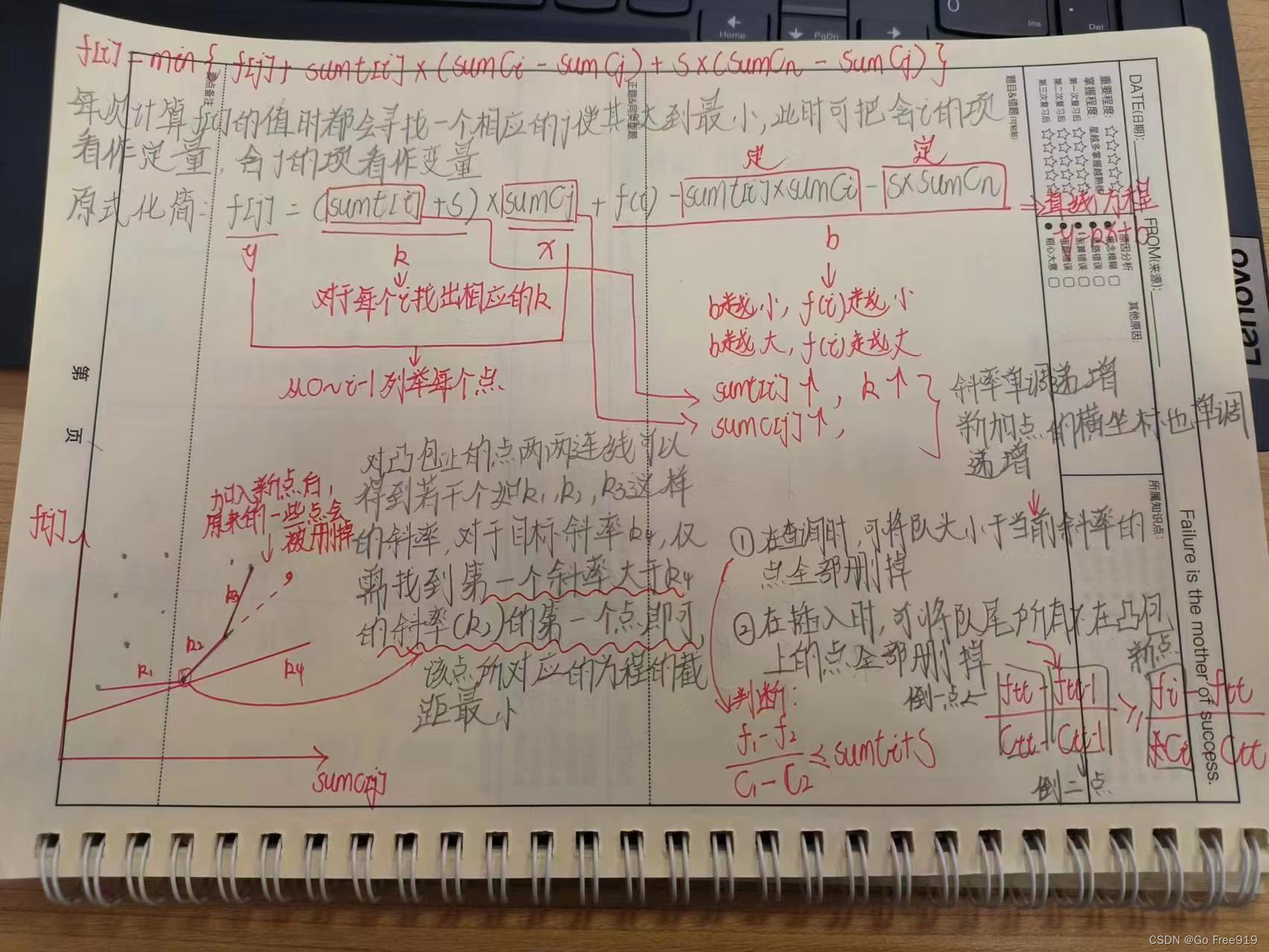
AcWing 301. 任务安排2【斜率优化DP模板】 - AcWing
