python中的matplotlib画散点图(数据分析与可视化)
python中的matplotlib画散点图(数据分析与可视化)
import numpy as np
import pandas as pd
import matplotlib.pyplot as pltpd.set_option("max_columns",None)
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False#任务三、堆积图
# x=np.arange(5)
# phone=pd.read_csv("D:\培训资料\matplotlib模块\任务驱动\素材\手机年销量.txt")
# phoneName=phone["品牌"]
# month6=phone["6月"]
# month7=phone["7月"]
# month8=phone["8月"]
# month9=phone["9月"]
# plt.stackplot(x,month6,month7,month8,month9,labels=["6月","7月","8月","9月"])
# plt.xticks(x,phoneName)
# plt.xlabel("品牌")
# plt.ylabel("销量")
# plt.legend(loc="upper right")
# plt.show()df1=pd.DataFrame({"names":["student"+str(i) for i in range(1,201) ],"sex":["男"]*200,"height":np.random.randint(160,199,200),"weight":np.random.randint(50,100,200)
})df2=pd.DataFrame({"names":["student"+str(i) for i in range(1,201) ],"sex":["女"]*200,"height":np.random.randint(150,175,200),"weight":np.random.randint(35,75,200)
})
data=pd.concat([df1,df2])
data=data.sample(frac=0.8)
print(data)
data1=data.query("sex=='男'")
data2=data.query("sex=='女'")
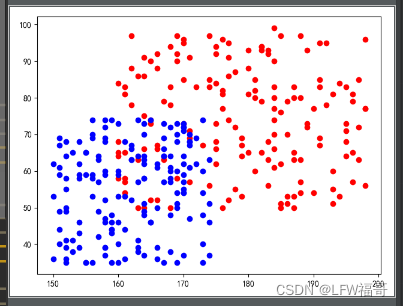
plt.scatter(data1["height"],data1["weight"],color="red")
plt.scatter(data2["height"],data2["weight"],color="blue")
plt.show()
效果图:
结束,再见
