【GUI】基于开关李雅普诺夫函数的非线性系统稳定(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
摘要:
如果李雅普诺夫函数已知,则可以稳定动态系统。然而,计算李雅普诺夫函数通常具有挑战性。本文采用了一种新的方法;它假设一个基本的类似李雅普诺夫的函数,然后试图在数值上减少李雅普诺夫值。如果控制工作在任何迭代中都没有效果,则切换类似李雅普诺夫的函数以尝试重新获得控制权。该方法在四个模拟系统上进行了测试,以对其有用性和局限性提供一些看法。高度耦合的三阶系统证明了该方法的一般适用性,最后考虑了机器人应用中3个电机的协调控制。
最初,Lyapunov理论被用于检验非线性系统的稳定性[1]。1983年,Artstein[2]开始使用Lyapunov理论进行控制器综合。他证明了Lyapunov函数存在当且仅当系统是可稳定的。
找到合适的李雅普诺夫函数可能很困难,但如果能找到,那么就可以用一个简单的公式计算出稳定控制的努力。除了Artstein的原始方法之外,当Lyapunov函数已知时,还有其他几种方法[3,4]来计算稳定控制努力。
许多研究者提出了寻找Lyapunov函数的创造性方法,包括[3-6]。然而,这些李亚普诺夫函数*处理了操作系统仅适用于本地,或者它们仅限于系统的一个子集。
一般来说,如何找到Lyapunov函数的问题仍然没有解决[4]。
Peleties[7]开创了分段动态系统的多个“Lyapunov”函数的概念,当整个感兴趣区域的单个Lyapunov函数未知或会导致过度保守的控制策略时,这是有用的。2013年,Sassano[8]提出了时变Lyapunov函数的概念。他的技术可以生成一个李雅普诺夫函数,而不需要解李雅普诺夫偏微分不等式,尽管它需要解另一个偏微分方程。所提出的方法在概念上类似于[7,8],因为它涉及一个动态的李雅普诺夫函数。它涉及到在默认值失去控制时在两个详尽的lyapunov类函数之间切换。与[8]一样,本文提出的方法不需要明确了解Lyapunov函数。与[7]相比,所提出的方法的优点是它不局限于特定形式的系统。与[8]相比,优点是该技术是全局适用的,并且不需要解偏微分方程。
📚2 运行结果
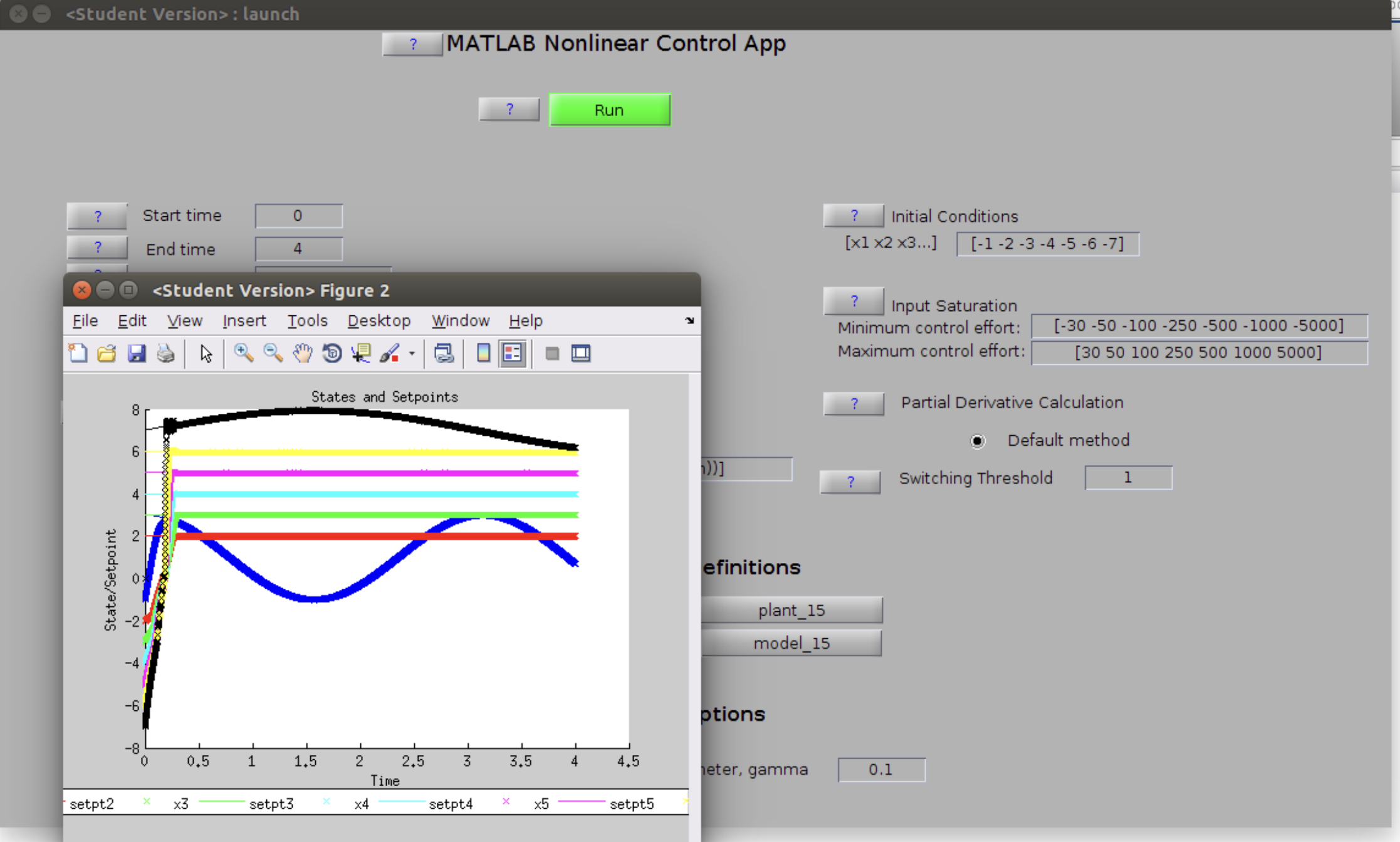
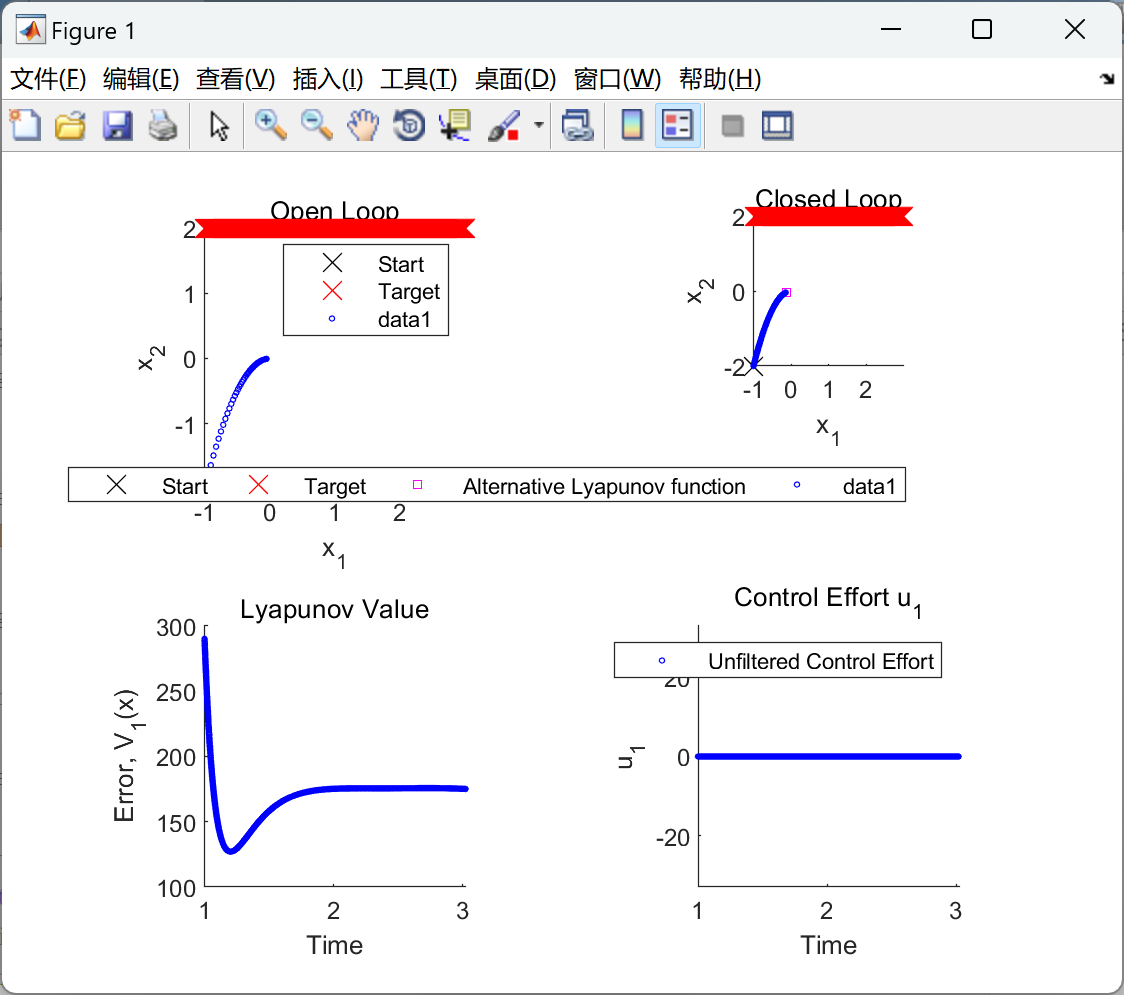
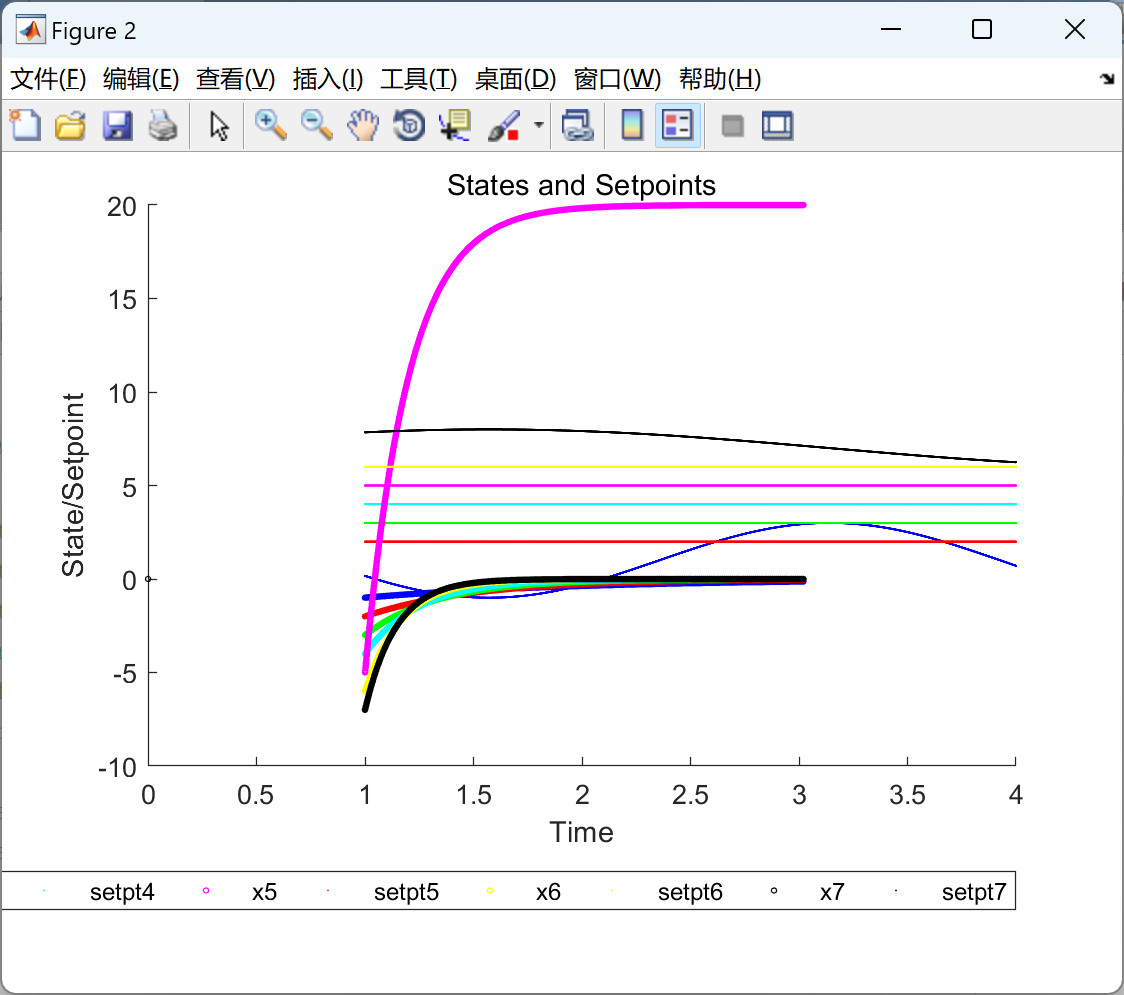
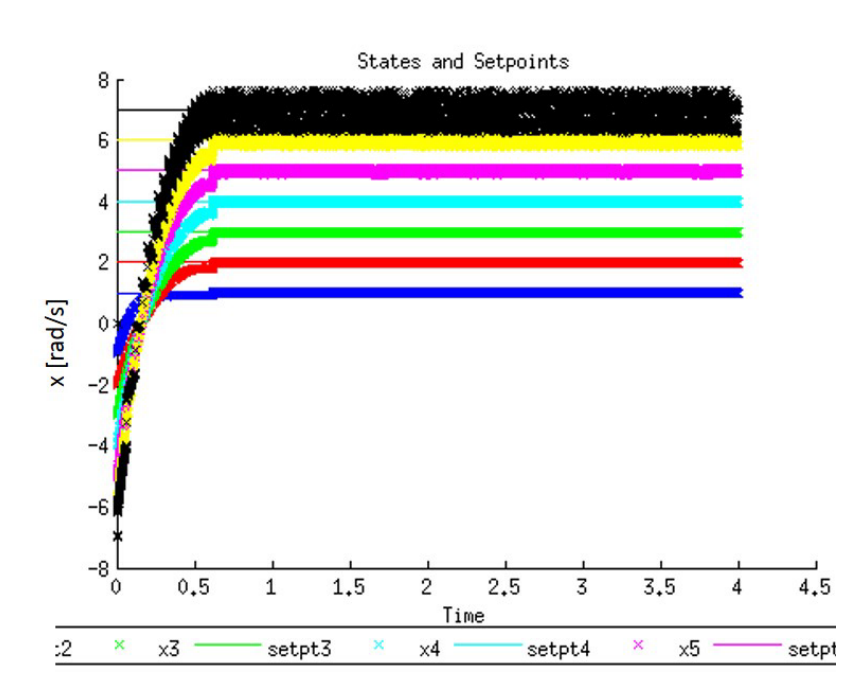
部分代码:
% Begin initialization code - DO NOT EDIT
gui_Singleton = 1;
gui_State = struct('gui_Name', mfilename, ...
'gui_Singleton', gui_Singleton, ...
'gui_OpeningFcn', @launch_OpeningFcn, ...
'gui_OutputFcn', @launch_OutputFcn, ...
'gui_LayoutFcn', [] , ...
'gui_Callback', []);
if nargin && ischar(varargin{1})
gui_State.gui_Callback = str2func(varargin{1});
end
if nargout
[varargout{1:nargout}] = gui_mainfcn(gui_State, varargin{:});
else
gui_mainfcn(gui_State, varargin{:});
end
% End initialization code - DO NOT EDIT
addpath(genpath(pwd))
% --- Executes just before launch is made visible.
function launch_OpeningFcn(hObject, eventdata, handles, varargin)
% This function has no output args, see OutputFcn.
% hObject handle to figure
% eventdata reserved - to be defined in a future version of MATLAB
% handles structure with handles and user data (see GUIDATA)
% varargin command line arguments to launch (see VARARGIN)
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。


