169. 多数元素(摩尔投票法) 题解
题目描述:169. 多数元素 - 力扣(LeetCode)
给定一个大小为
n的数组nums,返回其中的多数元素。多数元素是指在数组中出现次数 大于⌊ n/2 ⌋的元素。你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 :
输入:nums = [2,2,1,1,1,2,2] 输出:2
可以使用摩尔投票算法(Boyer-Moore Voting Algorithm)来解决这个问题,它是解决这种类型问题的一种高效算法。它的基本思想是通过不断消除不同元素对的投票来找到出现次数最多的元素。
-
摩尔投票算法
对于数组来说,数组中的每一个元素代表一个候选人,该数字出现的次数就是这个候选人的得票数,当候选人的投票数超过总票数的一半时,该候选人就能当选,也就找到了出现次数超过一半的数字:

算法思想:
因为各个候选人的关系是相互对立的,所以对于相互对立的得票可以相互抵消:
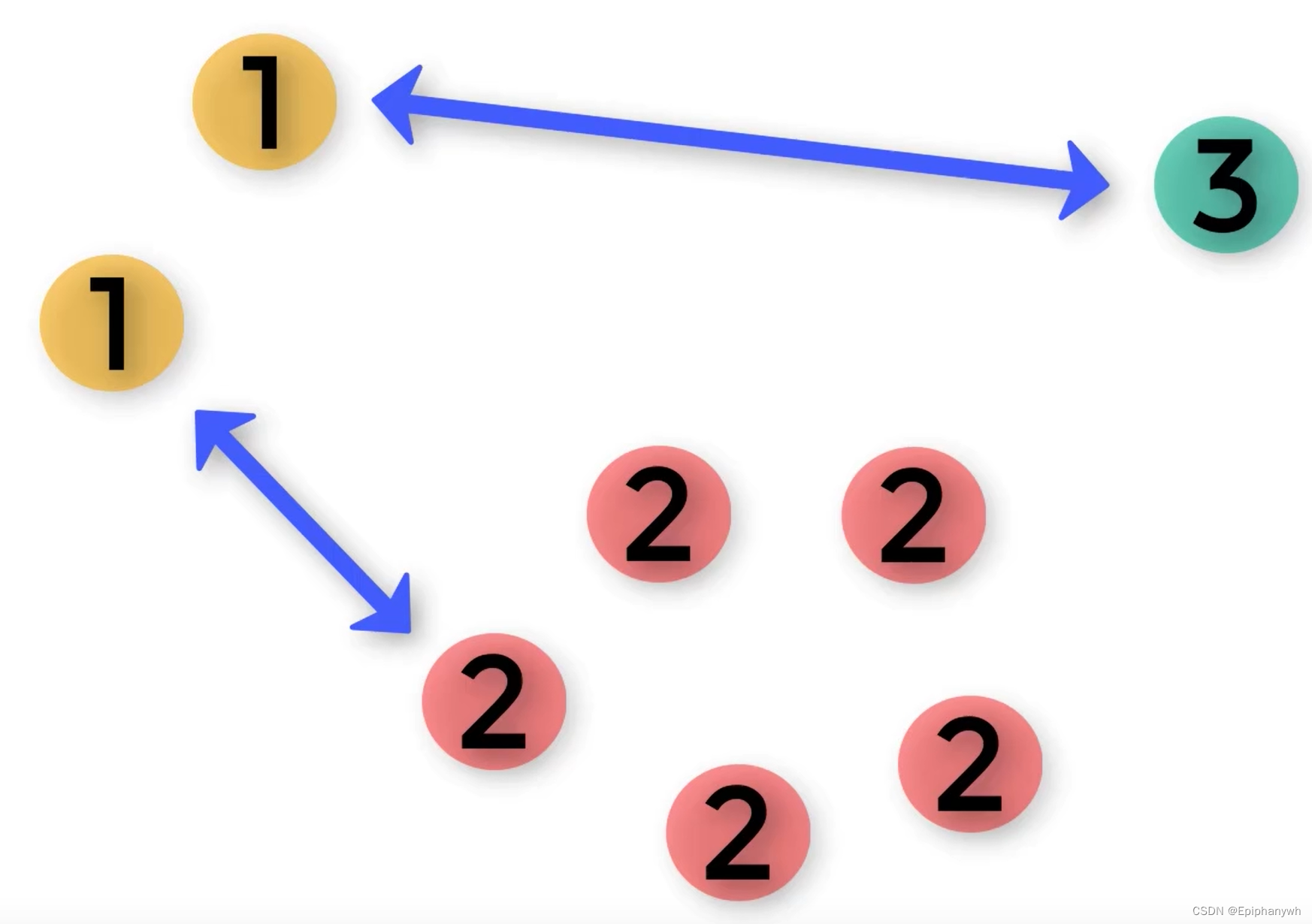

抵消到最后,还有票数的候选人就是当选人了。
当然,对立情况可能不是上面的那种情况:


显然,在这种情况下,也可以找到当选人,所以这个算法是合理的。
但是如果只是这样做,只能找到出现次数最多的数字,而这个数字出现的次数不一定超过一半,所以找到出现次数最多的数字后,还要再进行遍历判断出现次数是否超过一半。
让我通过一个实例来解释这个情况。假设数组为:
[3, 1, 3, 1, 2, 1, 2]。使用摩尔投票算法进行步骤演示:
- 初始化候选元素
candidate = 3,计数count = 1。- 遍历到元素
1,与候选元素不同,计数减1,count = 0。- 更新候选元素为
1,计数为1。- 遍历到元素
3,与候选元素不同,计数减1,count = 0。- 更新候选元素为
3,计数为1。- 遍历到元素
1,与候选元素不同,计数减1,count = 0。- 更新候选元素为
1,计数为1。- 遍历到元素
2,与候选元素不同,计数减1,count = 0。- 更新候选元素为
2,计数为1。在这个例子中,最后剩下的候选元素是
2,但是它并不是出现次数超过一半的元素。实际上,数组中没有出现次数超过一半的元素,因此摩尔投票算法无法在这种情况下找到多数元素。这正是为什么要在算法的最后一步进行验证的原因。通过验证候选元素的实际出现次数,我们可以确保它是否真的是多数元素。如果验证通过,那么候选元素就是多数元素;如果验证不通过,说明数组中没有多数元素。
在摩尔投票算法的应用中,验证是确保算法正确性的重要一步,尤其是在出现没有多数元素的情况下。
实现摩尔投票算法的具体步骤如下:
-
初始化候选元素和计数: 首先,初始化两个变量,一个用来存储候选元素(
candidate),另一个用来存储候选元素的计数(count)。初始时,将候选元素设为数组的第一个元素,将计数设为1。 -
遍历数组: 从数组的第二个元素开始,遍历整个数组。
- 如果当前元素与候选元素相同,将计数加1。
- 如果当前元素与候选元素不同,将计数减1。
-
更新候选元素: 在每次计数减到0时,说明之前的候选元素和其他元素抵消掉了,需要选择新的候选元素。此时,将当前元素作为新的候选元素,将计数重新设为1。
-
验证候选元素: 遍历完数组后,得到的候选元素可能是多数元素,但也可能不是。为了验证候选元素是否确实是多数元素,再次遍历整个数组,统计候选元素的实际出现次数。
-
确定多数元素: 如果候选元素的实际出现次数大于数组长度的一半(即超过 ⌊ n/2 ⌋ 次),则该候选元素可以被确认为多数元素;否则,说明没有多数元素存在。
用C语言实现的代码如下:
int majorityElement(int* nums, int numsSize) {int candidate = 0;int count = 0;for (int i = 0; i < numsSize; i++) {if (count == 0) {candidate = nums[i];count = 1;} else if (nums[i] == candidate) {count++;} else {count--;}}// 验证候选元素是否为多数元素count = 0;for (int i = 0; i < numsSize; i++) {if (nums[i] == candidate) {count++;}}if (count > numsSize / 2) {return candidate;}// 实际上,题目保证了一定存在多数元素,所以不会执行到这里return -1;
}注:摩尔算法不仅可以用来找到目标数字,如果目标元素是字符也是可以用该算法解题的。
本次内容到此结束了!如果你觉得这篇博客对你有帮助的话 ,希望你能够给我点个赞,鼓励一下我。感谢感谢……
参考资料:
【【算法】摩尔投票法】https://www.bilibili.com/video/BV1Co4y1y7LL?vd_source=564abed1c36a31978eb9de7cdc6668d2
