动态规划(基础)
一,背包问题
老规矩,上链接(http://t.csdn.cn/hEwvu)
(1)01背包问题
给定一个承重量为C的背包,n个重量分别为w1,w2,...,wn的物品,物品i放入背包能产生pi(>0)的价值(i=1,2,...,n)。每个物品要么整个放入背包,要么不放。要求找出最大价值的装包方案。
输入格式:
输入的第一行包含两个正整数n和C(1≤n≤20),第二行含n个正整数分别表示n个物品的重量,第三行含n个正整数分别表示n个物品放入背包能产生的价值。
输出格式:
在一行内输出结果,包括最大价值装包方案的价值、具体装包方案,用空格隔开。具体装包方案是n个物品的一个子集,用长度为n的0、1串表示(1表示对应物品被选中,0表示没有被选中)。如果这样的0、1串不唯一,取字典序最大的那个串。
输入样例:
4 9
2 3 4 5
3 4 5 7
输出样例:
12 1110
(注:1110 和0011都是价值最大的装包方案,取字典序最大的结果即为1110)
思想:最最经典的dp问题,画个图就明白了。
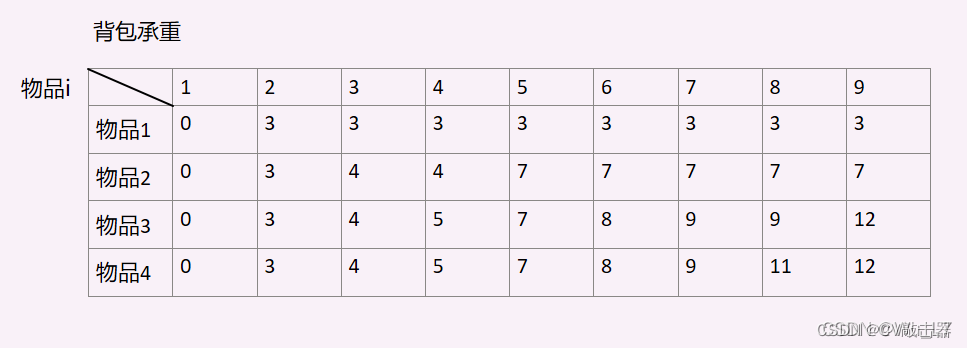
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N = 100;
int dp[N][N], w[N], val[N];int main()
{int n, m;cin >> n >> m;for (int i = 1; i <= n; i++) cin >> w[i];//重量for (int i = 1; i <= n; i++) cin >> val[i];//价值//求最大价值for (int i = 1; i <= n; i++) {for (int j = 0; j <= m; j++) {if (j >= w[i]) dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + val[i]);else dp[i][j] = dp[i - 1][j];}}cout << dp[n][m] << endl;//打印字典序for (int i = 1; i <= n; i++) {if (dp[i][m] - dp[i - 1][m] == 0) cout << "0";else cout << "1";}return 0;
}利用滚动数组优化,将二维数组降为一维数组
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int dp[N], t[N], val[N];int main()
{int time, n;cin >> time >> n;for (int i = 1; i <= n; i++) cin >> t[i] >> val[i];for (int i = 1; i <= n; i++) {//时间为j时的最大价值for (int j = time; j >= t[i]; j--) {//这里j倒序是为了防止重复拿同一件物品dp[j] = max(dp[j], dp[j - t[i]] + val[i]);}}cout << dp[time] << endl;return 0;
}(2)完全背包问题
有一个容积为 V 的背包,同时有 n 种物品,每种物品均有各自的体积 w 和价值 v,每种物品的数量均为无限个,求使用该背包最多能装的物品价值总和。
疯狂的采药 - 洛谷
思路:我们此时在多家一重循环表示同一种物品的数量就可以了,那么我们的递推式就变为
dp[i][j] = max( dp[i-1][j] , dp[i-1][ j - k*w[i] ] + k*v[i] )
AC代码
#include<iostream>
using namespace std;const int N=1005;
const int M=105;
int n,m,maxValue,temp;
int dp[M][N],t[M],v[M];int main()
{cin>>n>>m;for(int i=1;i<=m;i++) cin>>t[i]>>v[i];for(int i=1;i<=m;i++)for(int j=1;j<=n;j++){maxValue=0;for(int k=0;k*t[i]<=j;k++){temp=dp[i-1][j-k*t[i]]+k*v[i];if(temp>maxValue) maxValue=temp;}dp[i][j]=maxValue;}cout<<dp[m][n]<<endl;return 0;
}
这段代码是不能通过测试的,因为本题的数据比较大,而且我们用了三重循环,时间复杂度比较高,所以此方法不行。
同样的,我们使用滚动数组进行优化。
#include<bits/stdc++.h>
using namespace std;
const int N = 1e7 + 5;
long long dp[N], t[N], val[N];//数据过大,开长整型int main()
{int time, n;cin >> time >> n;for (int i = 1; i <= n; i++) cin >> t[i] >> val[i];for (int i = 1; i <= n; i++) {for (int j = t[i]; j <=time; j++) {dp[j] = max(dp[j], dp[j - t[i]] + val[i]);}}cout << dp[time] << endl;return 0;
}(3)
