【动态规划】回文串问题
文章目录
- 动态规划(回文串问题)
- 1. 回文子串
- 2. 最长回文子串
- 3. 回文串分割 IV
- 4. 分割回文串 ||
- 5. 最长回文子序列
- 6. 让字符串成为回文串的最小插入次数
动态规划(回文串问题)
1. 回文子串
题目链接
-
状态表示
f[i][j]表示 i 到 j 的子串当中是否是回文 -
状态转移方程

-
初始化
最初所有的内容都是0即可
-
填表
因为 i j 需要用 i + 1 来初始化,所以这个时候需要从下往上填表
-
返回值
返回整个dp 表里true 的数目就可以
AC代码:
class Solution
{
public:int countSubstrings(string s) {int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n));int ret = 0;for (int i = n - 1; i >= 0; i--){for (int j = i; j < n; j++){if (s[i] == s[j]){dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;}if (dp[i][j]) ret++;}}return ret;}
};
2. 最长回文子串
题目链接
如果需要求一个字符串当中的最长的回文子串,需要将所有的回文子串找到,然后再所有的回文子串里面找打一个最长的就可以了
可以参考上一个题目回文子串
AC代码:
class Solution
{
public:string longestPalindrome(string s) {// 找到所有的回文子串int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n));int begin = 0, len = 1;for (int i = n - 1; i >= 0; i--){for (int j = i; j < n; j++){if (s[i] == s[j]){dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;}if (dp[i][j] && j - i + 1 > len){begin = i;len = j - i + 1;}}}return s.substr(begin, len);}
};
3. 回文串分割 IV
题目链接
分析:如果暴力解题的话,i 和 j 可以把整个字符串分为3份,只需要遍历所有可能分为3份的情况直接判断是否都是回文串不就可以了。但是判断回文串需要花费时间,可以使用上面两道题的方法来判断是不是回文串
AC代码:
class Solution
{
public:bool checkPartitioning(string s) {int n = s.size();vector<vector<bool>> dp(n, vector<bool>(n));for (int i = n - 1; i >= 0; i--){for (int j = i; j < n; j++){if (s[i] == s[j]) dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : true;}}for (int i = 1; i < n - 1; i++){for (int j = i; j < n - 1; j++){if (dp[0][i - 1] && dp[i][j] && dp[j + 1][n - 1]) return true;}}return false;}
};
4. 分割回文串 ||
题目链接
-
状态表示
dp[i]表示0 到 i 之间,可以把所有子串都分割为回文串的最小次数 -
状态转移方程

-
初始化
所需初始位最大即可
-
填表
从左到右
-
返回值
AC代码:
class Solution
{
public:int minCut(string s) {int n = s.size();vector<vector<bool>> isPal(n, vector<bool>(n));for (int i = n - 1; i >= 0; i--){for (int j = i; j < n; j++){if (s[i] == s[j]) isPal[i][j] = i + 1 < j ? isPal[i + 1][j - 1] : true;}}vector<int> dp(n, INT_MAX);for (int i = 0; i < n; i++){if (isPal[0][i]) dp[i] = 0;else {for (int j = 1; j <= i; j++){if (isPal[j][i]) dp[i] = min(dp[i], dp[j - 1] + 1);}}}return dp[n - 1];}
};
5. 最长回文子序列
题目链接
-
状态表示
之前以某个位置为结尾来分析状态表示,如果dp[i]表示到i位置的最长回文子序列的长度来推导状态转移方程,只有长度是分析不出来状态转移方程。
dp[i][j]表示i j 这个区间内,最长的回文子序列的长度 -
状态转移方程
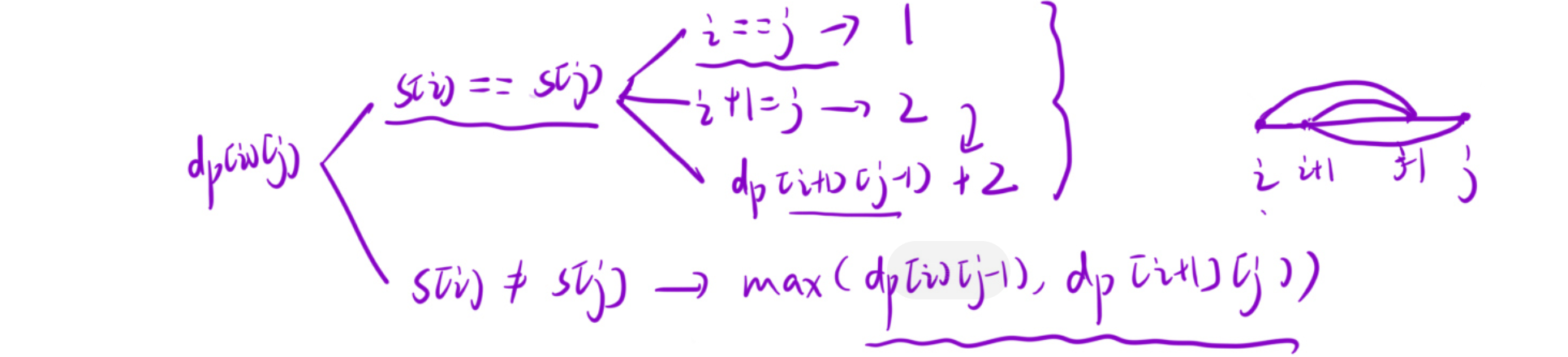
-
初始化
无需初始化
-
填表
因为需要用到 后面的值,所以填表需要从下到上,从左到右
-
返回值
AC代码:
class Solution
{
public:int longestPalindromeSubseq(string s) {int n = s.size();vector<vector<int>> dp(n, vector<int>(n));for (int i = n - 1; i >= 0; i--){for (int j = i; j < n; j++){if (s[i] == s[j]){dp[i][j] = i ==j ? 1 : dp[i + 1][j - 1] + 2;}else dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);}}return dp[0][n - 1];}
};
6. 让字符串成为回文串的最小插入次数
题目链接
-
状态表示
dp[i][j]表示:i 到 j 这个区间内,成为回文串的最小插入次数 -
状态转移方程
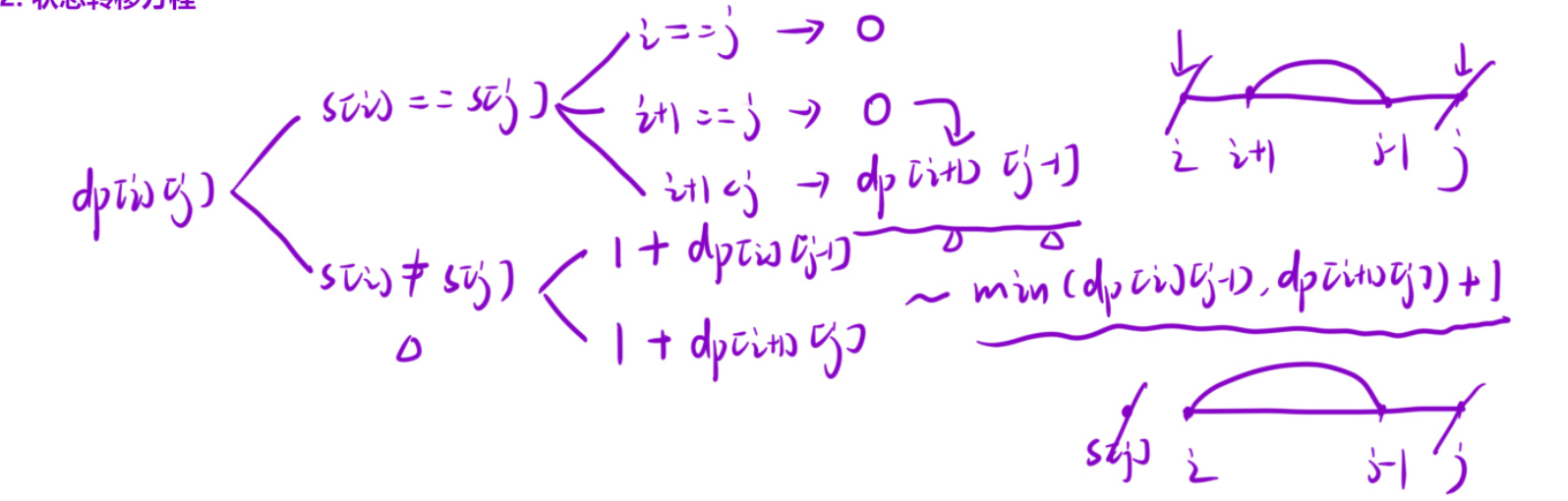
-
初始化
-
填表
从下往上,从左到右
-
返回值
AC代码:
class Solution
{
public:int minInsertions(string s) {int n = s.size();vector<vector<int>> dp(n, vector<int>(n));for (int i = n - 1; i >= 0; i--){for (int j = i; j < n; j++){if (s[i] == s[j]) dp[i][j] = i + 1 < j ? dp[i + 1][j - 1] : 0;else dp[i][j] = min(dp[i + 1][j], dp[i][j - 1]) + 1;}}return dp[0][n - 1];}
};
