第三章 图论 No.9有向图的强连通与半连通分量
文章目录
- 定义
- Tarjan求SCC
- 1174. 受欢迎的牛
- 367. 学校网络
- 1175. 最大半连通子图
- 368. 银河
定义
连通分量是无向图的概念,yxc说错了,不要被误导
强连通分量:在一个有向图中,对于分量中的任意两点u,v,一定能从u走到v,且能从v走到u。强连通分量是一些点的集合,若加入其他点,强连通分量中的任意两点就不能互相递达
半连通分量:在一个有向图中,对于分量中的任意两点u,v,一定存在从u走到v或者从v的路径
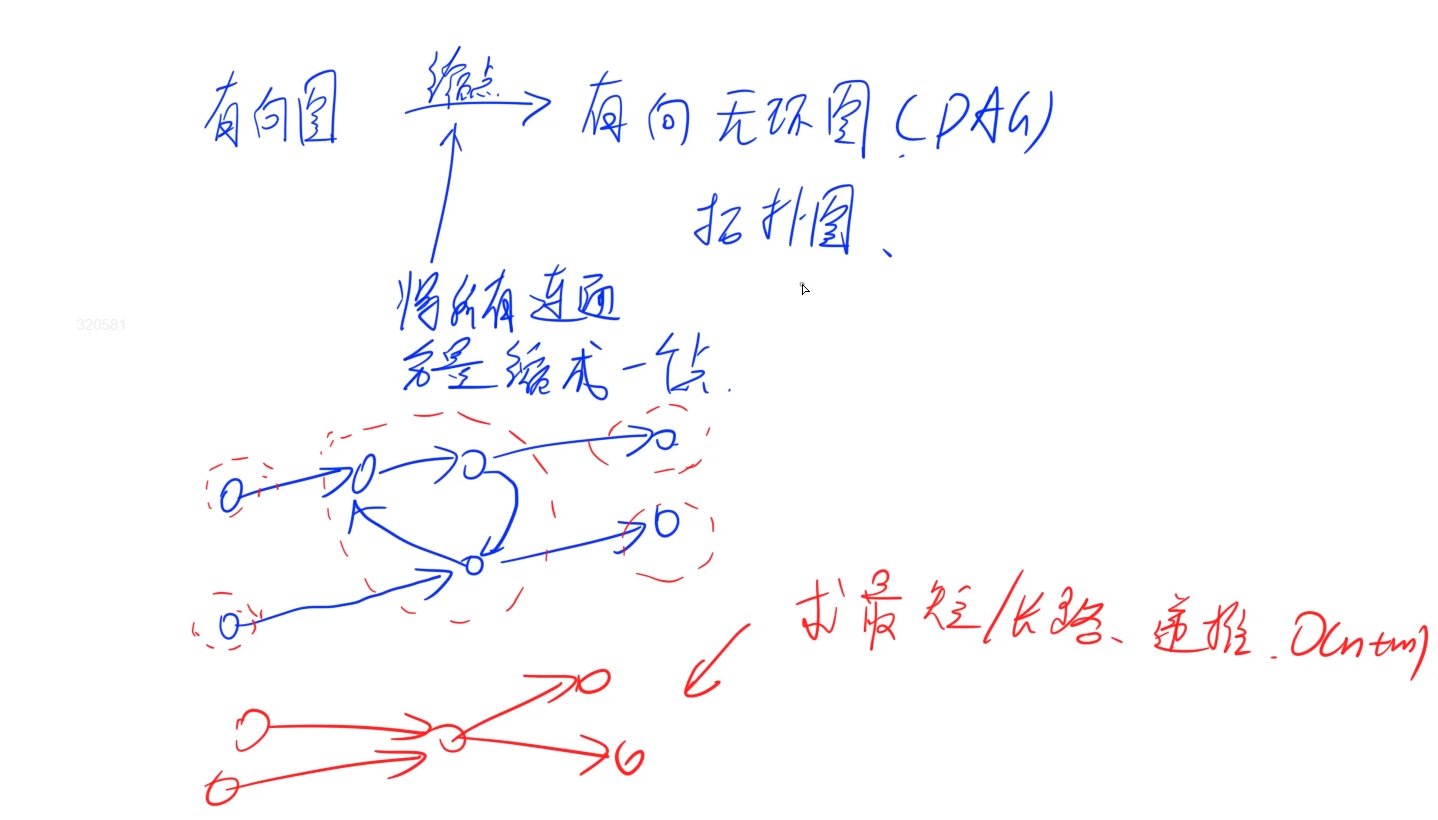
应用:通过缩点(将所有强连通分量缩成一个点)的方式,那么一个有向图就转换成了一个有向无环图DAG(拓扑图)
对于拓扑图,可以直接用bfs求最短路问题
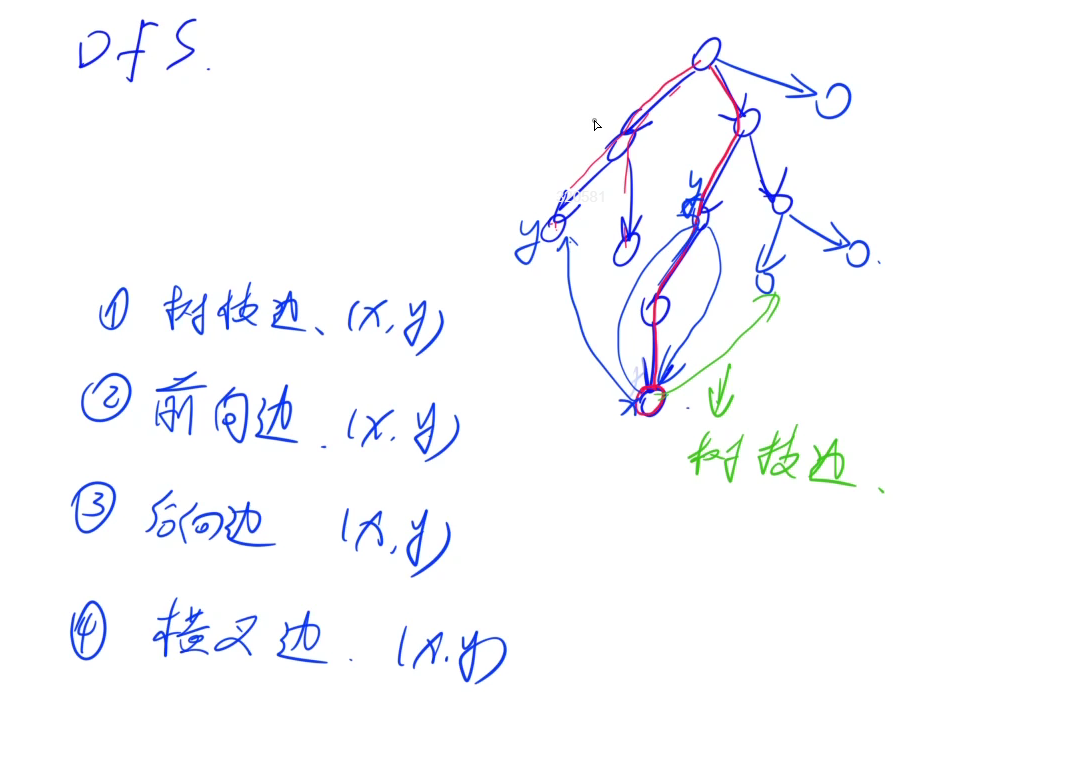
- 树枝边(x和y直接相连)
- 前向边(y是x的祖先节点)
- 后向边(前向边的反)
- 横叉边(指向已经遍历过的其他分支上的点)
树枝边是一种特殊的前向边
强连通分量简称scc,如何判断当前点是否在scc中?
- 存在一条后向边,指向祖先节点
- 先走横叉边,横叉边连接了后向边
无论如何,其一定能走到已经遍历过的祖先节点上
点可能存在自环,也是强连通分量(书上说自环不是强连通分量,但是为了算法的实现,将自环认为是强连通分量)
Tarjan求SCC
给定时间戳的概念,从小到大的时间为dfs的顺序
那树枝边的y一定比x大1,前向边的y一定大于等于x+1
后向边的y一定小于x,横叉边也是
对每个点定义两个时间戳:
dfs[u]表示遍历到u的时间
low[u]表示从u开始走,能遍历到的最小时间戳
若u是强连通分量的最高点,那么dfn[u] == low[u],即该点无法再往上走到其他点
板子中使用了两个栈,一个是系统函数栈,用来深搜。一个是自定义的栈,保存当前正在遍历的强连通分量中的所有点
板子 O ( n + m ) O(n + m) O(n+m):
void tarjan(int x)
{dfn[x] = low[x] = ++ tp;stk[ ++ tt] = x, st[x] = true;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!dfn[y]){tarjan(y);low[x] = min(low[x], low[y]);}else if (st[y]) low[x] = min(low[x], dfn[y]);}if (low[x] = dfn[x]){int y;++ cnt;do{y = stk[tt -- ], st[y] =false;id[y] = cnt;} while (y != x)}
}
缩点:遍历所有点,再遍历其所有邻点,若两点不在同一强连通分量中,将这两点之间添加一条边
强连通分量编号递减的顺序一定是拓扑序,求拓扑序一般使用bfs,除此之外还能使用dfs
遍历所有点,从入边为0的点开始,dfs其所有邻点,完成后将该点的编号加入序列中,序列的逆序就是拓扑序。因为每次进入序列的点一定无后继(或者后继节点已经进入序列的点)
不过,若图中存在多个入边为0的点,选择其一进行dfs即可,后续要在拓扑序开头加上这几个入边为0的点
1174. 受欢迎的牛
1174. 受欢迎的牛 - AcWing题库
反向建图,遍历所有点,用bfs判断当前点是否能递达其他所有点,时间复杂度为 O ( n 2 ) O(n^2) O(n2)
如果不反向建图,就要判断图中有几个出边为0的点,若有1个,那么这个点就是最受欢迎的,若有>1个,那么不存在最受欢迎的点,若有0个,说明图中一定存在环(强连通分量),环中的节点数量为受欢迎的点的数量
将所有的强连通分量(环)缩成一个点,此时图中出边为0的点的数量不可能为0
只要判断数量是否为1即可
若出边为的点的数量为1,说明该强连通分量中的所有点都是受欢迎的,统计环中节点的数量即可
#include <iostream>
#include <cstring>
using namespace std;const int N = 1e4 + 10, M = 5e4 + 10;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], tp, cnt;
int stk[N], tt; bool st[N];
int dout[N], id[N], sz[N]; // 每个强连通分量中的节点数量
int n, m;void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}void tarjan(int x)
{stk[ ++ tt] = x, st[x] = true;dfn[x] = low[x] = ++ tp;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!dfn[y]){tarjan(y);low[x] = min(low[x], low[y]);}else if (st[y]) low[x] = min(low[x], dfn[y]);}if (dfn[x] == low[x]){int y;cnt ++ ;do {y = stk[tt -- ], st[y] = false;id[y] = cnt;sz[cnt] ++ ;} while (y != x);}
}int main()
{memset(h, -1, sizeof(h));scanf("%d%d", &n, &m);int x, y;for (int i = 0; i < m; ++ i ){scanf("%d%d", &x, &y);add(x, y);}for (int i = 1; i <= n; ++ i )if (!dfn[i]) tarjan(i);for (int x = 1; x <= n; ++ x ) for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];int a = id[x], b = id[y]; if (a != b) dout[a] ++ ;}int ans = 0, t = 0;for (int i = 1; i <= cnt; ++ i )if (!dout[i]){t ++ ;ans = sz[i];if (t > 1){ans = 0;break;}}printf("%d\n", ans);return 0;
}
debug到死的一道题:
首先tp要前置++,虽然tp是时间戳的概念,但是在数组中作为下标还对应着节点编号
最后检查dout数组中,循环从1到cnt,不是从1到n,也不是从1到cnt - 1,因为cnt不是后置++,而是++完再使用
else if (st[y]) low[x] = min(low[x], dfn[y]);写歪了,写成
else if (st[y]) low[x] = min(low[x], dfn[x]);
367. 学校网络
367. 学校网络 - AcWing题库
将所有强连通分量缩点后,图中入度为0的点为第一问的答案
第二问是:任何一个有向无环图,需要加几条边才能使之成为一个强连通分量
结论:假设有向无环图有P个入度为0的点,Q个出度为0的点,需要加max(P, Q)个点
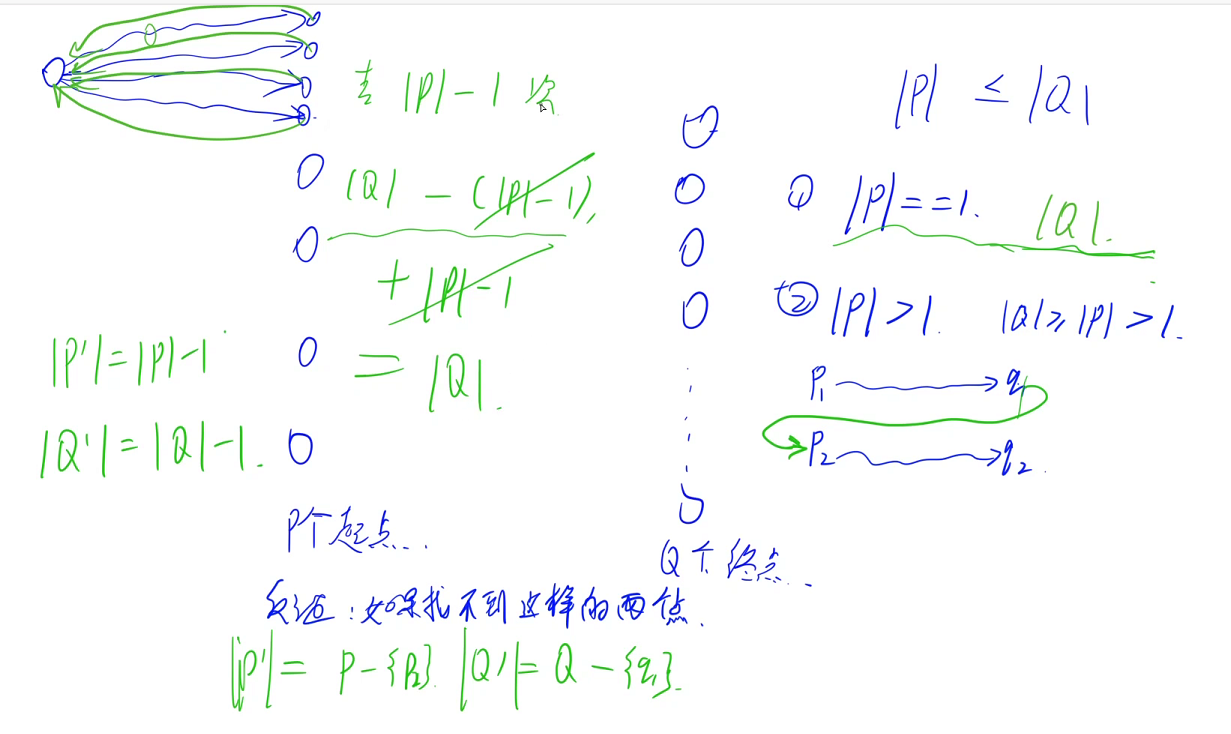
设起点的集合为P,终点的集合为Q
假设 ∣ P ∣ < = ∣ Q ∣ |P| <= |Q| ∣P∣<=∣Q∣,若 ∣ P ∣ > ∣ Q ∣ |P| > |Q| ∣P∣>∣Q∣,建个反图即可
考虑两种情况, ∣ P ∣ = 1 |P| = 1 ∣P∣=1,此时将所有的终点向起点连一条边,即 Q Q Q条边。此时从起点一定能走到所有点,从中间点一定能走到终点,而终点一定能走到起点,从而走完所有点。所以此时图中任意一点能走完图中所有点
∣ P ∣ > 1 |P| > 1 ∣P∣>1时,在终点与起点之间连一条边(尽可能与无法到达该终点的起点连线),直到起点的数量为1(每次连完边后,起点数量与终点数量都减一),此时的情况为 ∣ P ∣ = 1 |P|=1 ∣P∣=1的情况 ∣ Q ∣ − ( ∣ P ∣ − 1 ) |Q|-(|P|-1) ∣Q∣−(∣P∣−1)条边即可,由于已经连了 ∣ P ∣ − 1 |P|-1 ∣P∣−1条边,所以总共需要连的边数为 ∣ Q ∣ |Q| ∣Q∣
#include <iostream>
#include <cstring>
using namespace std;const int N = 110, M = N * N;
int h[N], e[M], ne[M], idx;
int dfn[N], low[N], tp, cnt;
int id[N], stk[N], tt;
bool st[N];
int din[N], dout[N];
int n, t;void add(int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}void tarjan(int x)
{st[x] = true, stk[ ++ tt] = x;dfn[x] = low[x] = ++ tp;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!dfn[y]){tarjan(y);low[x] = min(low[x], low[y]);}else if (st[y]) low[x] = min(low[x], dfn[y]);}if (dfn[x] == low[x]){int y;cnt ++ ;do {y = stk[tt -- ], st[y] = false;id[y] = cnt;} while (x != y);}
}int main()
{memset(h, -1, sizeof(h));scanf("%d", &n);int y;for (int x = 1; x <= n; ++ x )while (scanf("%d", &y), y)add(x, y);for (int i = 1; i <= n; ++ i )if (!dfn[i])tarjan(i);int u = 0;for (int x = 1; x <= n; ++ x)for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];int a = id[x], b = id[y];if (a != b) din[b] ++, dout[a] ++ ;}int in = 0, out = 0;for (int i = 1; i <= cnt; ++ i ){if (!din[i]) in ++ ;if (!dout[i]) out ++ ;}if (cnt == 1) printf("%d\n%d\n", in, 0);else printf("%d\n%d\n", in, max(in, out));return 0;
}
debug:dfs的次数与缩点后入度为0的点的数量不一定相同
缩点后的图中可能存在入度和出度都为0的点,所以判断要用两个if
最后要注意,缩点后的图只有一个连通分量时,需要特判输出
1175. 最大半连通子图
1175. 最大半连通子图 - AcWing题库
首先,强连通分量一定是半连通分量,所以可以先找出图中所有强连通分量
用tarjan将图缩点,得到由强连通分量组成的有向无环图,此时再找出极大半连通分量(有向图中点最多的一条路径),可以按照拓扑序递推,找一条最长路
由于每个点都是强连通分量,计算最长路的节点数量时,需要累加所有“节点”(强连通分量)中的节点数量,只能在按照拓扑序递推最长路时,将边权设置为分量中的点数
若缩点后的两点之间存在多条边,因为导出子图一定会将和点有关的所有边选择,所以边数不同不能算不同的半连通子图,半连通分量中不存在只选择两点之间一部分边的情况,因此点数不同才算不同的半连通子图
由于我们找最长路时,需要使用边的权重,重边将影响最长路的求解,所以在建立缩点后的图时要注意给边判重
边的权重是分量中点的数量,与这些两点之间的重边没有关系,因此只需要在两点之间建立一条边
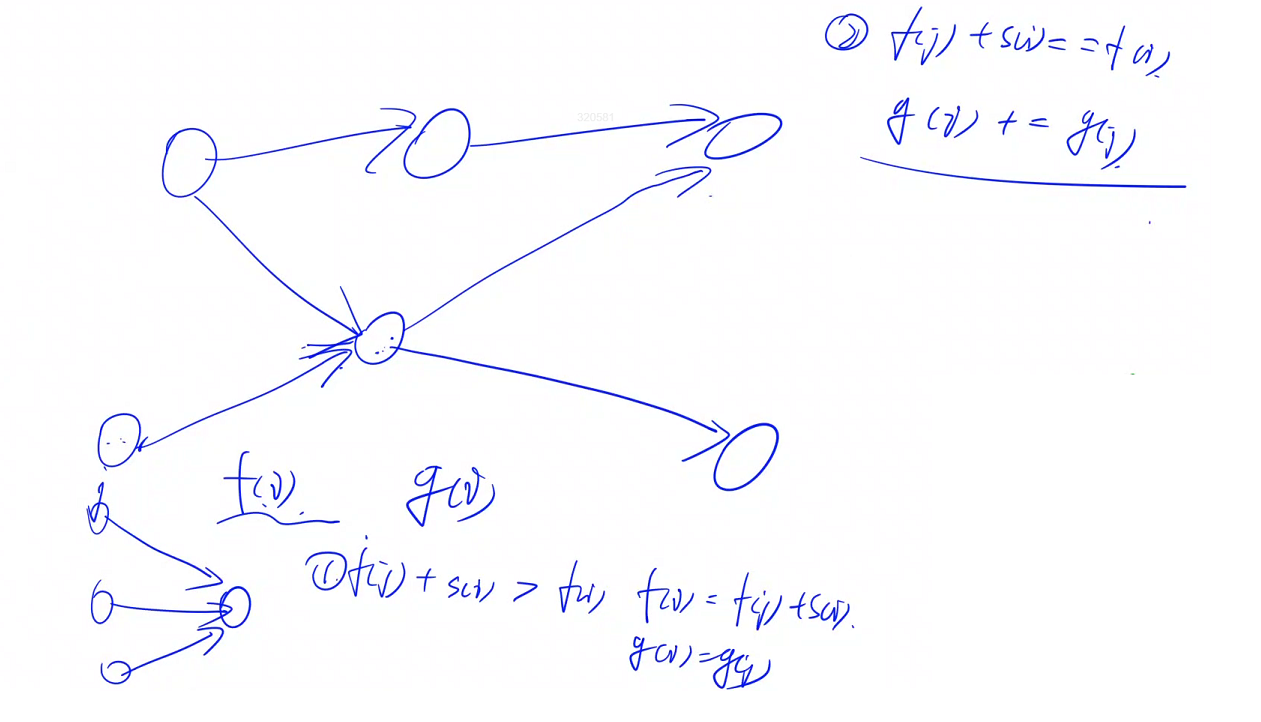
缩点建图完成后,就是递推求最长路。由于缩点的递归顺序是拓扑序的逆序,所以我们逆着遍历缩点的顺序,按照拓扑序递推求最长路即可。注意不仅要记录最长路的权值还要记录最长路的数量,分别对应最大半连通子图中点的数量以及最大半连通子图的数量
#include <iostream>
#include <cstring>
#include <unordered_set>
using namespace std;typedef long long LL;
const int N = 1e5 + 10, M = 2e6 + 10;
int h[N], hs[N], e[M], ne[M], idx;
int dfn[N], low[N], cnt, tp;
int stk[N], tt; bool st[N];
unordered_set<LL> s;
int sz[N], id[N];
int f[N], g[N];
int n, m, X;void add(int h[], int x, int y)
{e[idx] = y, ne[idx] = h[x], h[x] = idx ++ ;
}void tarjan(int x)
{dfn[x] = low[x] = ++ tp;st[x] = true, stk[ ++ tt] = x;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!dfn[y]){tarjan(y);low[x] = min(low[x], low[y]);}else if (st[y]) low[x] = min(low[x], dfn[y]);}if (dfn[x] == low[x]){int y;cnt ++ ;do {y = stk[tt -- ], st[y] = false;id[y] = cnt;sz[cnt] ++ ;} while (x != y);}
}int main()
{memset(h, -1, sizeof(h));memset(hs, -1, sizeof(hs));scanf("%d%d%d", &n, &m, &X);int x, y;for (int i = 0; i < m; ++ i ){scanf("%d%d", &x, &y);add(h, x, y);}for (int i = 1; i <= n; ++ i )if (!dfn[i]) tarjan(i);for (int x = 1; x <= n; ++ x )for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];int a = id[x], b = id[y];if (a != b){LL t = a * 100000ll + b;if (!s.count(t)) {add(hs, a, b);s.insert(t);}}}for (int x = cnt; x; -- x ){if (!f[x]) f[x] = sz[x], g[x] = 1;for (int i = hs[x]; i != -1; i = ne[i]){int y = e[i];if (f[y] < f[x] + sz[y]){f[y] = f[x] + sz[y];g[y] = g[x];}else if (f[y] == f[x] + sz[y]) g[y] = (g[x] + g[y]) % X;}}int maxf = 0, sum = 0;for (int i = 1; i <= cnt; ++ i ){if (f[i] > maxf){maxf = f[i];sum = g[i];}else if (f[i] == maxf) sum = (sum + g[i]) % X;}printf("%d\n%d\n", maxf, sum);return 0;
}
debug:unordered_set比set快很多,当然,也比unordered_map快
最后的最长路递推没有按照拓扑序(cnt的逆序)
没有去重,递推时要遍历缩点后的图
递推时:
if (f[y] < f[x] + sz[y])
{f[y] = f[x] + sz[y];g[y] = g[x];
}
写成了g[y] = f[x],手滑了,但是这种错误真的超难debug
368. 银河
368. 银河 - AcWing题库
很直接的不等式关系,一眼差分约束,首先转换不等式关系,由于题目要求最小值,所以要用最短路,所有不等式要转换成>=的形式
- A >= B, B >= A
- B >= A + 1
- A >= B
- A >= B + 1
- B >= A
并且题目提供了一个边界, x i > = 1 x_i >= 1 xi>=1,转换成 x i > = x 0 + 1 x_i >= x_0 + 1 xi>=x0+1
那么 x 0 x_0 x0为虚拟源点,与所有点有一条边权为1的边,从 x 0 x_0 x0开始遍历,一定能遍历所有的点,也一定能遍历所有的边
所以从 x 0 x_0 x0为源点,用spfa求最长路,并且判断负环(无解)即可
这题和1169. 糖果一样,解法一样,数据一样,但是时间限制卡的很死。用sfpa求最长路与正环会超时
正解是:用线性时间复杂度的tarjan求强连通分量,判断每个强连通分量是否是正环。由于图中只有权值为0和1的边,环中权值为0是个零环,只要有一条边的权值为1,那么该强连通分量就是正环,返回无解
接着按照拓扑序求最长路即可
#include <iostream>
#include <cstring>
using namespace std;typedef long long LL;
const int N = 1e5 + 10, M = 4e5 + 10;
int h[N], hs[N], e[M], ne[M], w[M], idx;
int dfn[N], low[N], cnt, tp;
int stk[N], tt; bool st[N];
int id[N], dis[N], sz[N];
int n, m;void add(int h[], int x, int y, int d)
{e[idx] = y, ne[idx] = h[x], w[idx] = d, h[x] = idx ++ ;
}void tarjan(int x)
{dfn[x] = low[x] = ++ tp;st[x] = true, stk[ ++ tt] = x;for (int i = h[x]; i != -1; i = ne[i]){int y = e[i];if (!dfn[y]){tarjan(y);low[x] = min(low[x], low[y]);}else if (st[y]) low[x] = min(low[x], dfn[y]);}if (dfn[x] == low[x]) {int y;++ cnt;do {y = stk[tt -- ], st[y] = false;id[y] = cnt;sz[cnt] ++ ;} while (x != y);}
}int main()
{memset(h, -1, sizeof(h));memset(hs, -1, sizeof(hs));scanf("%d%d", &n, &m);int t, x, y;for (int i = 0; i < m; ++ i ){scanf("%d%d%d", &t, &x, &y);if (t == 1) add(h, x, y, 0), add(h, y, x, 0);else if (t == 2) add(h, x, y, 1);else if (t == 3) add(h, y, x, 0);else if (t == 4) add(h, y, x, 1);else add(h, x, y, 0);}for (int i = 1; i <= n; ++ i ) add(h, 0, i, 1);for (int i = 0; i <= n; ++ i ) if (!dfn[i]) tarjan(i);for (int x = 0; x <= n; ++ x )for (int i = h[x]; i != -1; i = ne[i]){int y= e[i];int a = id[x], b = id[y];if (a == b && w[i] == 1){puts("-1");return 0;}else if (a != b) add(hs, a, b, w[i]);}for (int x = cnt; x; -- x ){for (int i = hs[x]; i != -1; i = ne[i] ){int y = e[i];dis[y] = max(dis[y], dis[x] + w[i]);}}LL sum = 0;for (int i = 1; i <= cnt; ++ i ) sum += (LL)sz[i] * dis[i];printf("%lld\n", sum);return 0;
}
debug:递推时又是没有遍历hs,缩点后的图
虚拟源点的边没有提前建,之前做sfpa时习惯在spfa里直接将所有边入队了
同时,tarjan需要遍历的点为0n之间的所有点,不是1n
最后计算总和时,连通分量乘以距离才是正解
