第十三次CCF计算机软件能力认证
第一题:跳一跳
近来,跳一跳这款小游戏风靡全国,受到不少玩家的喜爱。
简化后的跳一跳规则如下:玩家每次从当前方块跳到下一个方块,如果没有跳到下一个方块上则游戏结束。
如果跳到了方块上,但没有跳到方块的中心则获得 1 分;跳到方块中心时,若上一次的得分为 1 分或这是本局游戏的第一次跳跃则此次得分为 2 分,否则此次得分比上一次得分多两分(即连续跳到方块中心时,总得分将 +2,+4,+6,+8…)。
现在给出一个人跳一跳的全过程,请你求出他本局游戏的得分(按照题目描述的规则)。
输入格式
输入包含多个数字,用空格分隔,每个数字都是 1,2,0 之一,1 表示此次跳跃跳到了方块上但是没有跳到中心,2 表示此次跳跃跳到了方块上并且跳到了方块中心,0 表示此次跳跃没有跳到方块上(此时游戏结束)。
输出格式
输出一个整数,为本局游戏的得分(在本题的规则下)。
数据范围
对于所有评测用例,输入的数字不超过 30 个,保证 0 正好出现一次且为最后一个数字。
输入样例:
1 1 2 2 2 1 1 2 2 0输出样例:
22
解题思路:
直接模拟
#include<iostream>using namespace std;int main()
{int last = 1;int n;int res = 0;while(cin >> n){if(n == 0) break;if(n == 1) res ++ , last = 1;else {if(last == -1 || last == 1) res += 2 , last = 2;else res += (last + 2) , last += 2;}}cout << res << endl;return 0;
}第二题:碰撞的小球
数轴上有一条长度为 L(L 为偶数)的线段,左端点在原点,右端点在坐标 L 处。
有 n 个不计体积的小球在线段上,开始时所有的小球都处在偶数坐标上,速度方向向右,速度大小为 1 单位长度每秒。
当小球到达线段的端点(左端点或右端点)的时候,会立即向相反的方向移动,速度大小仍然为原来大小。
当两个小球撞到一起的时候,两个小球会分别向与自己原来移动的方向相反的方向,以原来的速度大小继续移动。
现在,告诉你线段的长度 L,小球数量 n ,以及 n 个小球的初始位置,请你计算 t 秒之后,各个小球的位置。
提示
因为所有小球的初始位置都为偶数,而且线段的长度为偶数,可以证明,不会有三个小球同时相撞,小球到达线段端点以及小球之间的碰撞时刻均为整数。
同时也可以证明两个小球发生碰撞的位置一定是整数(但不一定是偶数)。
输入格式
输入的第一行包含三个整数 n,L,t,用空格分隔,分别表示小球的个数、线段长度和你需要计算 t 秒之后小球的位置。
第二行包含 n 个整数 a1,a2,…,an,用空格分隔,表示初始时刻 n 个小球的位置。
输出格式
输出一行包含 n 个整数,用空格分隔,第 i 个整数代表初始时刻位于 ai 的小球,在 t 秒之后的位置。
数据范围
对于所有评测用例,1≤n≤100,1≤t≤100,2≤L≤1000,0<ai<L。L 为偶数。
保证所有小球的初始位置互不相同且均为偶数。
输入样例1:
3 10 5 4 6 8输出样例1:
7 9 9样例1解释
初始时,三个小球的位置分别为 4,6,8。
一秒后,三个小球的位置分别为 5,7,9。
两秒后,第三个小球碰到墙壁,速度反向,三个小球位置分别为 6,8,10。
三秒后,第二个小球与第三个小球在位置 9 发生碰撞,速度反向(注意碰撞位置不一定为偶数),三个小球位置分别为 7,9,9。
四秒后,第一个小球与第二个小球在位置8发生碰撞,速度反向,第三个小球碰到墙壁,速度反向,三个小球位置分别为 8,8,10。
五秒后,三个小球的位置分别为 7,9,9。
输入样例2:
10 22 30 14 12 16 6 10 2 8 20 18 4输出样例2:
6 6 8 2 4 0 4 12 10 2
解题思路:
使用结构体存储小球当前的状态 +1 表示向右 , -1表示向左
第一种情况,到边界的时候将方向置反即可
第二种情况,正常运动时
(1)下一秒的时候没有遇到球,当前位置加上方向信息
(2)下一秒的时候遇到球的时候,将两个球反向
#include<iostream>
#include<cstring>using namespace std;const int N = 110;
int n , l , t;
struct node
{int idx , dir; // +1 表示向右 , -1表示向左
}a[N];void change()
{int cnt[10 * N];memset(cnt , -1 , sizeof cnt);for(int i = 0;i < n;i ++){if(a[i].idx == 0 || a[i].idx == l) a[i].dir = -a[i].dir;if(cnt[a[i].idx] != -1){a[i].dir = -a[i].dir;a[cnt[a[i].idx]].dir = -a[cnt[a[i].idx]].dir;}else cnt[a[i].idx] = i;}for(int i = 0;i < n;i ++)a[i].idx += a[i].dir;
}int main()
{cin >> n >> l >> t;for(int i = 0;i < n;i ++){int x;cin >> x;a[i] = {x , 1};}while(t --){change();}for(int i = 0;i < n;i ++)cout << a[i].idx << " ";return 0;
}第三题:URL映射
题目略
解题思路:
其中三个重要的函数
(1)get_number函数:获取字符串中的数字并且返回该数的字符串
(2)get函数:将每一条URL映射解析
- 如果匹配,那么返回一个vector存储的是对应URL请求的解析后的结果
- 如果不匹配, 那么返回一个空的vector
(3)work函数:尽心处理每一条URL请求
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>using namespace std;const int N = 110;int n, m;
struct Url
{string path, name;
}url[N];string get_number(string& str)
{string res;for (auto c: str)if (c >= '0' && c <= '9')res += c;else{res.clear();return res;}// 去掉前导0int k = 0;while (k + 1 < res.size() && res[k] == '0') k ++ ;return res.substr(k);
}vector<string> get(string& path, string& str)
{vector<string> res(1);int i, j;for (i = 1, j = 1; i < path.size() && j < str.size();){int u = i + 1, v = j + 1;while (u < path.size() && path[u] != '/') u ++ ;while (v < str.size() && str[v] != '/') v ++ ;string a = path.substr(i, u - i), b = str.substr(j, v - j);if (a == "<str>"){res.push_back(b);i = u + 1, j = v + 1;}else if (a == "<int>"){auto t = get_number(b);if (t.empty()){res.clear();return res;}res.push_back(t);i = u + 1, j = v + 1;}else if (a == "<path>"){res.push_back(str.substr(j));return res;}else if (a != b){res.clear();return res;}else i = u + 1, j = v + 1;}if (i - path.size() != j - str.size()) res.clear();return res;
}void work(string& str)
{for (int i = 0; i < n; i ++ ){auto res = get(url[i].path, str);if (res.size()){cout << url[i].name;for (int j = 1; j < res.size(); j ++ )cout << ' ' << res[j];cout << endl;return;}}puts("404");
}int main()
{cin >> n >> m;for (int i = 0; i < n; i ++ ) cin >> url[i].path >> url[i].name;while (m -- ){string str;cin >> str;work(str);}return 0;
}第四题:棋局评估
Alice 和 Bob 正在玩井字棋游戏。
井字棋游戏的规则很简单:两人轮流往 3×3 的棋盘中放棋子,Alice 放的是
X,Bob 放的是O,Alice执先。当同一种棋子占据一行、一列或一条对角线的三个格子时,游戏结束,该种棋子的持有者获胜。
当棋盘被填满的时候,游戏结束,双方平手。
Alice 设计了一种对棋局评分的方法:
- 对于 Alice 已经获胜的局面,评估得分为(棋盘上的空格子数+1);
- 对于 Bob 已经获胜的局面,评估得分为 -(棋盘上的空格子数+1);
- 对于平局的局面,评估得分为 0;
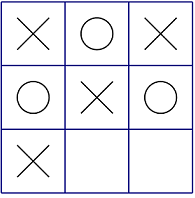
例如上图中的局面,Alice 已经获胜,同时棋盘上有 2 个空格,所以局面得分为 2+1=3。
由于 Alice 并不喜欢计算,所以他请教擅长编程的你,如果两人都以最优策略行棋,那么当前局面的最终得分会是多少?
输入格式
输入的第一行包含一个正整数 T,表示数据的组数。
每组数据输入有 3 行,每行有 3 个整数,用空格分隔,分别表示棋盘每个格子的状态。0 表示格子为空,1 表示格子中为
X,2 表示格子中为O。保证不会出现其他状态。保证输入的局面合法。(即保证输入的局面可以通过行棋到达,且保证没有双方同时获胜的情况)
保证输入的局面轮到 Alice 行棋。
输出格式
对于每组数据,输出一行一个整数,表示当前局面的得分。
数据范围
1≤T≤5
输入样例:
3 1 2 1 2 1 2 0 0 0 2 1 1 0 2 1 0 0 2 0 0 0 0 0 0 0 0 0输出样例:
3 -4 0样例解释
第一组数据:
Alice 将棋子放在左下角(或右下角)后,可以到达问题描述中的局面,得分为 3。
3 为 Alice 行棋后能到达的局面中得分的最大值。
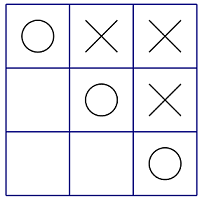
第二组数据:
Bob 已经获胜(如图),此局面得分为 −(3+1)=−4。
第三组数据:
井字棋中若双方都采用最优策略,游戏平局,最终得分为 0。
解题思路:
其中有三个函数
(1)dfs函数:求最终的得分,使用深度优先搜索进行遍历每一种情况
(2)cal函数:计算每一个状态时的空格的数量
(3)check函数:对于一个人判断是否是一个获胜的情况
#include<iostream>using namespace std;const int N = 5 , INF = 1e8;
int g[N][N];bool check(int x)
{// 判断行列for(int i = 0;i < 3;i ++){int s = 0;for(int j = 0;j < 3;j ++)if(g[i][j] == x) s ++;if(s == 3) return true;s = 0;for(int j = 0;j < 3;j ++)if(g[j][i] == x) s ++;if(s == 3) return true;}if(g[0][0] == x && g[1][1] == x && g[2][2] == x) return true;if(g[2][0] == x && g[1][1] == x && g[0][2] == x) return true;return false;
}int cal()
{int s = 0;// 计算空格的数量for(int i = 0;i < 3;i ++)for(int j = 0;j < 3;j ++)if(!g[i][j]) s ++;// alice赢if(check(1)) return s + 1;// bob赢if(check(2)) return -(s + 1);// 平局if(!s) return 0;return INF;
}int dfs(int u)
{int t = cal();if(t != INF) return t;if(!u){// alice 搜索最大值 X 使用1表示int res = -INF;for(int i = 0;i < 3;i ++)for(int j = 0;j < 3;j ++)if(!g[i][j]){g[i][j] = 1;res = max(res , dfs(1));g[i][j] = 0;}return res;}else{// bob 搜索最小值 O 使用2表示int res = INF;for(int i = 0;i < 3;i ++)for(int j = 0;j < 3;j ++)if(!g[i][j]){g[i][j] = 2;res = min(res , dfs(0));g[i][j] = 0;}return res;}
}int main()
{int t;cin >> t;while(t --){for(int i = 0;i < 3;i ++)for(int j = 0;j < 3;j ++)cin >> g[i][j];// 0表示alice 1表示bobcout << dfs(0) << endl;}
}第五题:二次求和
线段树+前缀和+树
(不会)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;typedef long long LL;
const int N = 100010, M = N * 2, MOD = 1e9 + 7;int n, m, L, R;
int w[N];
int h[N], father[N], e[M], ne[M], idx;
int depth[N], fa[N][17];
int path[N], d[N], que[N];
int pos[N], root[N];
bool st[N];
int tr[N];
struct Node
{int d, w, id;bool operator< (const Node& t) const{return d < t.d;}
}q[N], p[N];inline void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}inline int lowbit(int x)
{return x & -x;
}inline void update(int x, int v, int k)
{for (int i = x; i <= k; i += lowbit(i)) tr[i] = (tr[i] + v) % MOD;
}inline int query(int x, int k)
{x = min(x, k);int res = 0;for (int i = x; i > 0; i -= lowbit(i)) res = (res + tr[i]) % MOD;return res;
}void bfs()
{memset(depth, 0x3f, sizeof depth);depth[0] = 0, depth[1] = 1;int hh = 0, tt = 0;que[0] = 1;while (hh <= tt){int t = que[hh ++ ];for (int i = h[t]; ~i; i = ne[i]){int j = e[i];if (depth[j] > depth[t] + 1){depth[j] = depth[t] + 1;que[ ++ tt] = j;fa[j][0] = t;for (int k = 1; k <= 16; k ++ )fa[j][k] = fa[fa[j][k - 1]][k - 1];}}}
}inline int lca(int a, int b)
{if (depth[a] < depth[b]) swap(a, b);for (int k = 16; k >= 0; k -- )if (depth[fa[a][k]] >= depth[b])a = fa[a][k];if (a == b) return a;for (int k = 16; k >= 0; k -- )if (fa[a][k] != fa[b][k]){a = fa[a][k];b = fa[b][k];}return fa[a][0];
}void dfs(int u, int fa)
{d[u] = (d[fa] + path[u]) % MOD;for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (j == fa) continue;dfs(j, u);}
}int get_size(int u, int fa)
{if (st[u]) return 0;int res = 1;for (int i = h[u]; ~i; i = ne[i])if (e[i] != fa)res += get_size(e[i], u);return res;
}int get_wc(int u, int fa, int tot, int& wc)
{if (st[u]) return 0;int sum = 1, ms = 0;for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (j == fa) continue;int t = get_wc(j, u, tot, wc);ms = max(ms, t);sum += t;}ms = max(ms, tot - sum);if (ms <= tot / 2) wc = u;return sum;
}void get_dist(int u, int fa, int dist, int sum, int& qt)
{if (st[u]) return;q[ ++ qt] = {dist, sum, u};for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (j != fa)get_dist(j, u, dist + 1, (sum + w[j]) % MOD, qt);}
}inline int get(Node a[], int k, int limit, int wu, int& pu)
{sort(a + 1, a + k + 1);static int sum[N];int res = 0;for (int i = 1; i <= k; i ++ ) sum[i] = (sum[i - 1] + a[i].w) % MOD;for (int i = 1, j = k; i < j; i ++ ){while (j > i && a[j].d + a[i].d - 1 > limit) j -- ;if (j > i && a[j].d + a[i].d - 1 <= limit){res = (res + (LL)sum[j] - sum[i] + (LL)(j - i) * a[i].w - (LL)wu * (j - i)) % MOD;pu = (pu + j - i) % MOD;}}return res;
}int dfs_path(int u, int fa, int dist, int maxd)
{if (st[u]) return 0;int res = (query(R + 1 - dist, maxd) - query(L - dist, maxd)) % MOD;if (dist >= L && dist <= R) res = (res + 1) % MOD;for (int i = h[u]; ~i; i = ne[i]){int j = e[i];if (j != fa)res = (res + dfs_path(j, u, dist + 1, maxd)) % MOD;}path[u] = (path[u] + res) % MOD;return res;
}int calc(int u)
{if (st[u]) return 0;get_wc(u, -1, get_size(u, -1), u);st[u] = true;int res = 0, pt = 0;if (L <= 1 && R >= 1) res = w[u], path[u] = (path[u] + 1) % MOD;int cnt = 0, maxd = 0;for (int i = h[u]; ~i; i = ne[i]){int j = e[i], qt = 0;if (st[j]) continue;get_dist(j, -1, 2, (w[u] + w[j]) % MOD, qt);int pR = 0, pL = 0;res = (res - (LL)(get(q, qt, R, w[u], pR) - get(q, qt, L - 1, w[u], pL))) % MOD;path[u] = (path[u] - (LL)(pR - pL)) % MOD;pos[ ++ cnt] = pt + 1; // 每一段开头root[cnt] = j; // 每一段的根节点for (int k = 1; k <= qt; k ++ ){if (q[k].d >= L && q[k].d <= R){res = (res + q[k].w) % MOD;path[u] = (path[u] + 1) % MOD; // 只计算从u到当前点的}p[ ++ pt] = q[k];maxd = max(maxd, q[k].d);}}pos[cnt + 1] = pt + 1; // 哨兵for (int i = 1; i <= maxd; i ++ ) tr[i] = 0;for (int i = 1; i <= pt; i ++ ) update(p[i].d, 1, maxd); // 插入树状数组中for (int i = 1; i <= cnt; i ++ ){int l = pos[i], r = pos[i + 1] - 1;for (int j = l; j <= r; j ++ ) update(p[j].d, -1, maxd); // 将当前子树中的节点删掉dfs_path(root[i], u, 2, maxd);for (int j = l; j <= r; j ++ ) update(p[j].d, 1, maxd); // 将当前子树中的节点添加回来}int pR = 0, pL = 0;res = (res + (LL)get(p, pt, R, w[u], pR) - get(p, pt, L - 1, w[u], pL)) % MOD;path[u] = (path[u] + (LL)pR - pL) % MOD;for (int i = h[u]; ~i; i = ne[i]) res = (res + calc(e[i])) % MOD;return res;
}int main()
{int T;scanf("%d", &T);while (T -- ){scanf("%d%d%d%d", &n, &m, &L, &R);memset(h, -1, sizeof h), idx = 0;memset(path, 0, sizeof path);for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);for (int i = 2; i <= n; i ++ ){int p;scanf("%d", &p);add(i, p), add(p, i);father[i] = p;}memset(st, 0, sizeof st);int res = calc(1);dfs(1, 0);bfs();while (m -- ){int a, b, c;scanf("%d%d%d", &a, &b, &c);int p = lca(a, b);int sum = (d[a] + (LL)d[b] - d[p] * 2 + path[p]) * c % MOD;res = ((res + sum) % MOD + MOD) % MOD;printf("%d\n", res);}}return 0;
}