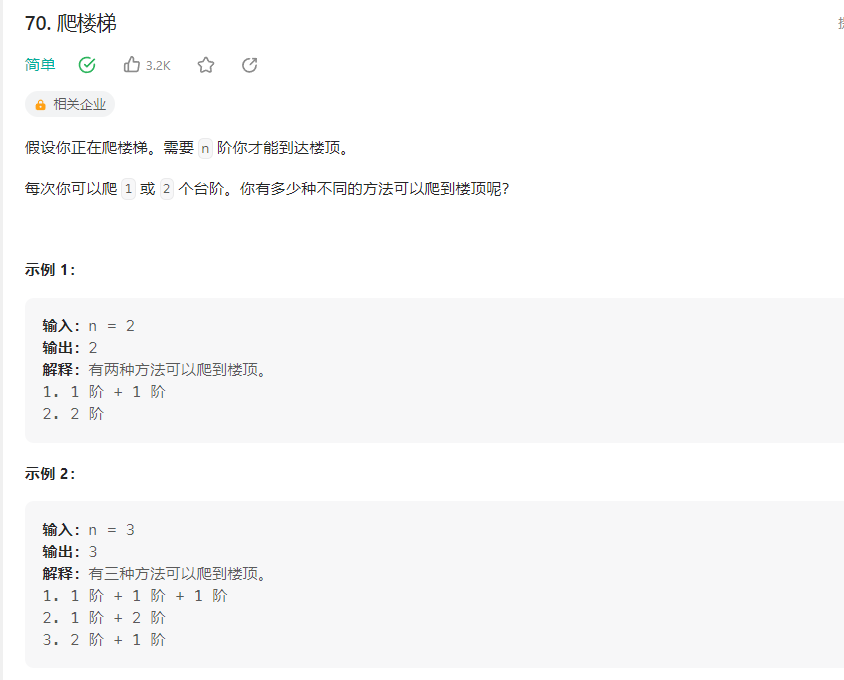
leetcode每日一练-第70题-爬楼梯
一、思路
动态规划
二、解题方法
使用一个动态规划数组 dp 来记录到达每个台阶的不同方法数。初始情况下,当台阶数为 1 时,方法数为 1,当台阶数为 2 时,方法数为 2。然后,我们从第 3 阶开始逐步计算每一阶的方法数,方法数等于前一阶和前两阶方法数之和。最终,我们返回 dp[n],即到达 n 阶台阶的不同方法数。
三、code
class Solution {
public:int climbStairs(int n) {if(n<=2){return n;}vector<int> dp(n+1,0);//使用一个动态规划数组 dp 来记录到达每个台阶的不同方法数//是一个用来存储动态规划状态的向量(数组),其中 n + 1 是数组的大小,初始化值都为 0。//在动态规划中,状态通常用一个数组(或向量)来表示,每个元素对应不同状态的解。在这个例子中,dp 数组的长度是 n + 1,表示有 n + 1 个不同的状态,索引从 0 到 n。dp[1]=1;dp[2]=2;//在动态规划的过程中,你会填充 dp 数组,其中 dp[i] 表示到达第 i 阶楼梯的不同方法数。最终,当你求解完整个数组后,你需要返回 dp[n],即到达楼顶的不同方法数。for(int i=3;i<=n;++i){dp[i]=dp[i-1]+dp[i-2];//从第 3 阶开始逐步计算每一阶的方法数,方法数等于前一阶和前两阶方法数之和}return dp[n];//dp[n] 表示到达楼顶的不同方法数,其中 n 是楼梯的总阶数}
};=========================================================================学到的知识:
①
动态规划(Dynamic Programming,简称 DP)是一种解决问题的算法思想,通常用于求解具有重叠子问题和最优子结构性质的问题。它通过将问题分解为子问题并存储子问题的解,以避免重复计算,从而提高算法的效率。
动态规划常用于求解最优化问题,比如最短路径、最长公共子序列、背包问题等。它的核心思想是将原问题拆分为更小的子问题,然后通过解决子问题来解决原问题。在解决子问题时,动态规划会使用一种记忆化的方法,将子问题的解保存在数据结构中,以便后续直接获取,避免重复计算。
动态规划通常分为自顶向下和自底向上两种方式:
-
自顶向下:从大问题开始,逐步分解为子问题,然后通过递归或记忆化搜索来解决子问题。
-
自底向上:从小问题开始,逐步构建出更大的问题的解,通常采用迭代的方式,从子问题的解推导出原问题的解。
动态规划在算法设计和优化中具有广泛应用,能够有效地提高问题的求解效率,但也需要合理的状态定义、状态转移方程和边界条件来确保正确性。
②
vector<int> dp(n + 1, 0); 是一个用来存储动态规划状态的向量(数组),其中 n + 1 是数组的大小,初始化值都为 0。
在动态规划中,状态通常用一个数组(或向量)来表示,每个元素对应不同状态的解。在这个例子中,dp 数组的长度是 n + 1,表示有 n + 1 个不同的状态,索引从 0 到 n。
