当前位置：首页 > news >正文

c#: NetTopologySuite凹凸多边形计算

news 2025/9/16 21:59:29

环境：

.net 6.0
NetTopologySuite 2.5.0
vs2022
平面二维

一、夹角计算

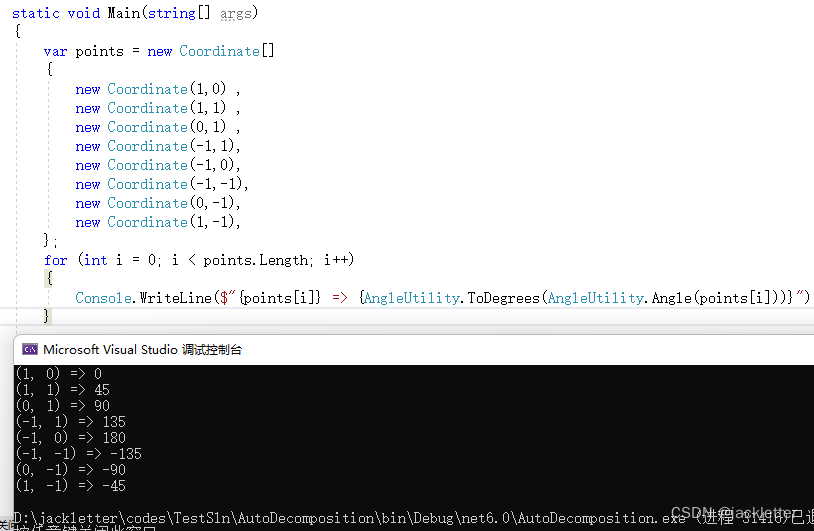
1.1 计算向量与x轴正方向的夹角

方法: AngleUtility.Angle(Coordinate p)

下图上的t2即为p，之所以这么写是为了和AngleUtility.AngleBetweenOriented做比较

注意：

结果逆时针为正，顺时针为负；
相对于x轴；

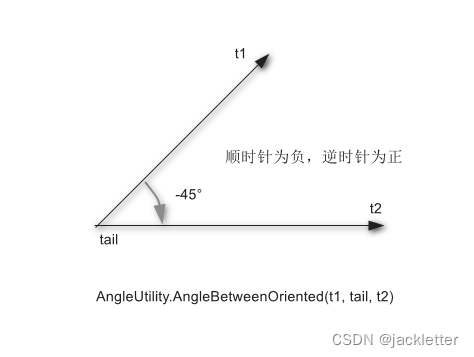
在这里插入图片描述

实例：
在这里插入图片描述

1.2 计算两条线段的夹角（区分方向）

方法: AngleUtility.AngleBetweenOriented(Coordinate tip1, Coordinate tail, Coordinate tip2)
注意：

结果逆时针为正，顺时针为负；
∠t1 tail t2；

在这里插入图片描述
实例：

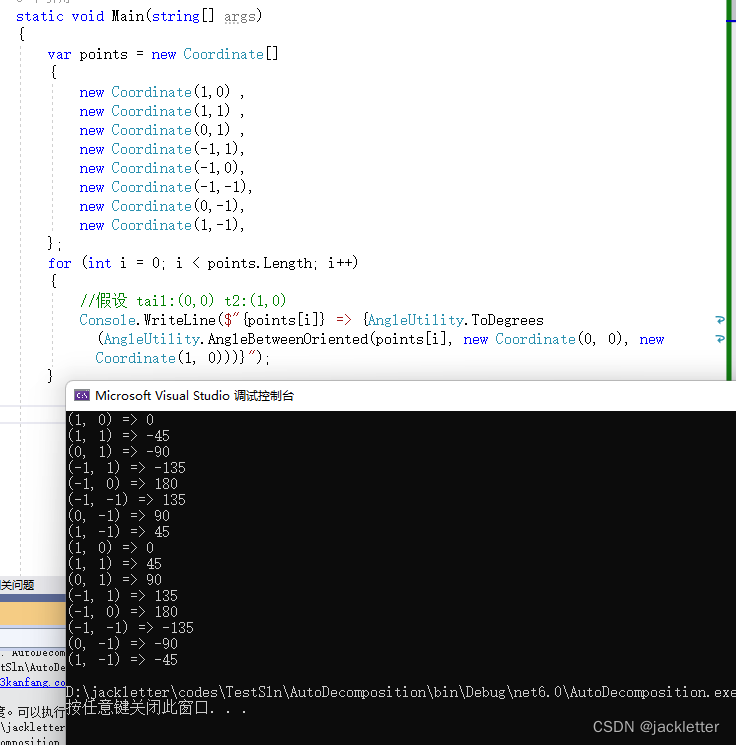
1.3 计算两条线段的夹角（不区分方向）

方法: AngleUtility.AngleBetween(Coordinate tip1, Coordinate tail, Coordinate tip2)
由于不考虑方向，两个线段的夹角总是处在 [0,180°) 范围内。
不在画图显示。

二、检测一个环是否是简单的(IsSimple)

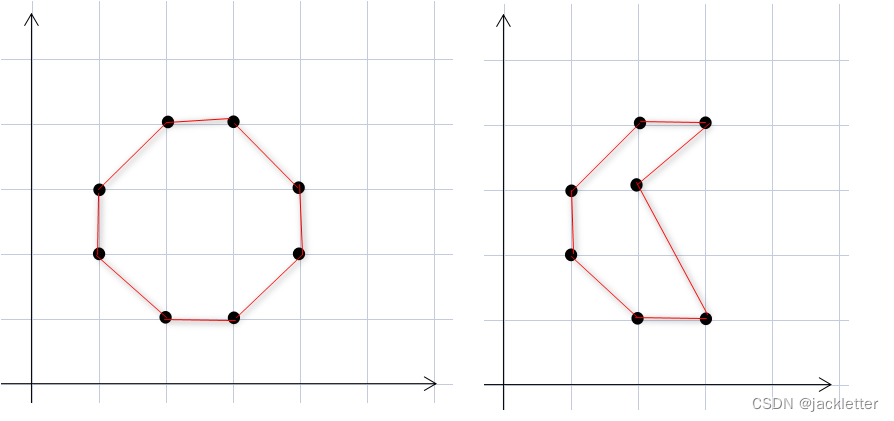
2.1 简单的示例（IsSimple=true）：

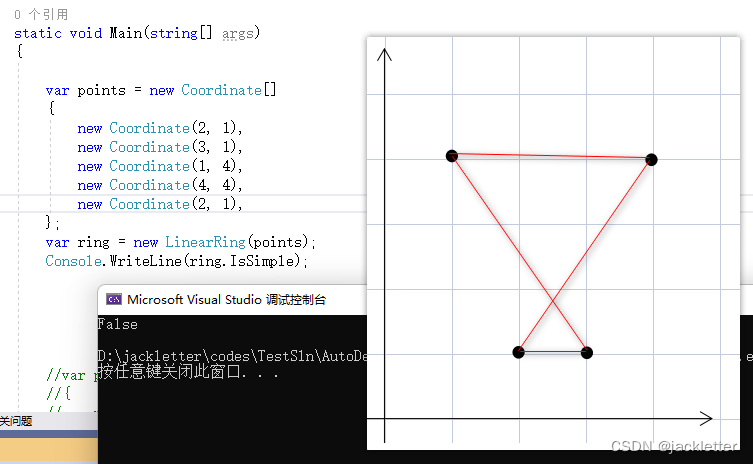
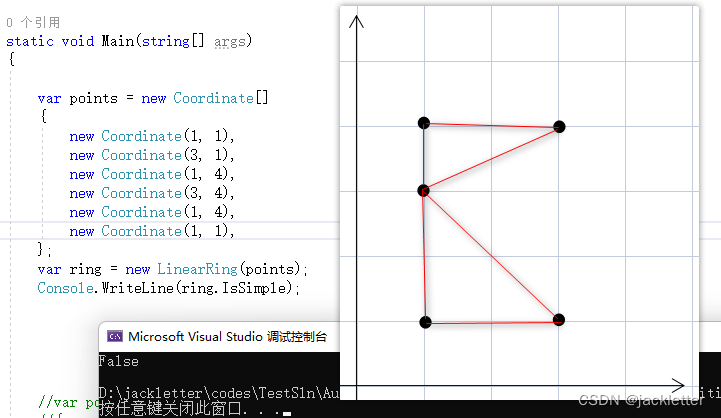
在这里插入图片描述

2.2 复杂的示例（IsSimple=false）：

在这里插入图片描述

三、多边形的凹凸(convex/concave) 和顺(Clockwise)/逆(CounterClockwise)时针

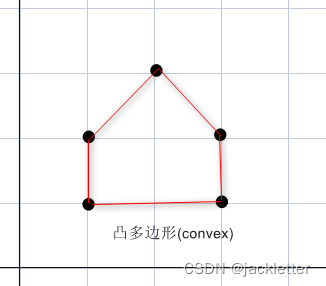
3.1 多边形的凹凸定义：

凸多边形（convex）： 所有的内角都小于180°；
凹多边形（concave）： 至少有一个内角大于180°；

示例：
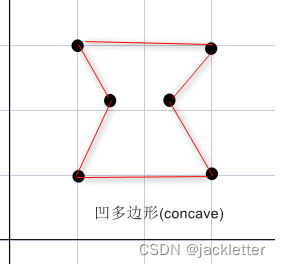
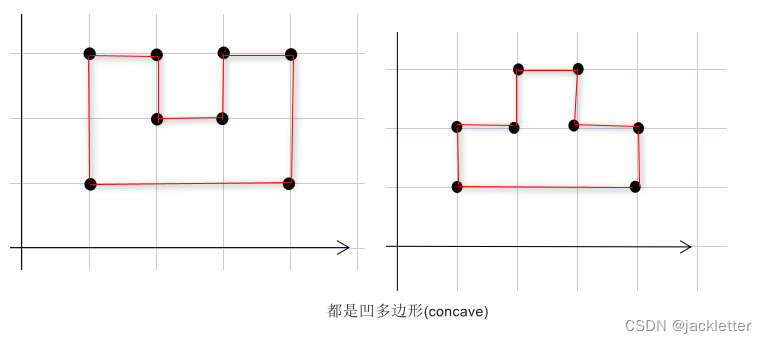
在这里插入图片描述

3.2 多边形的顺逆时针

因为多边形是一个环状的东西，所以在平面上可以用顺逆时针表示它的方向，这在很多计算方法中有用。

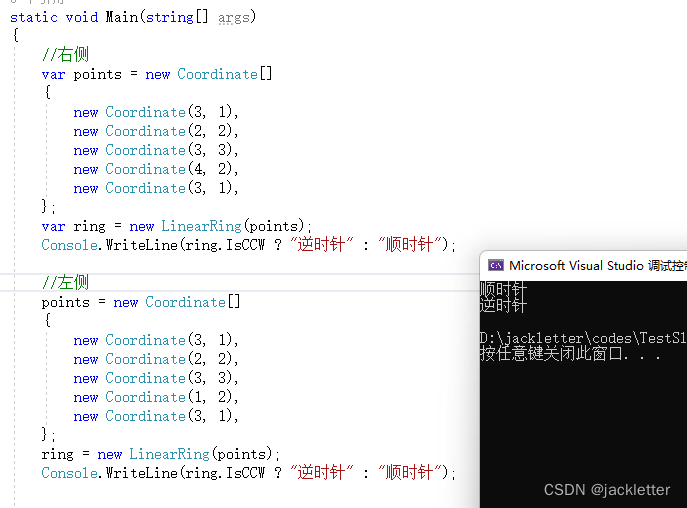
多边形的方向应该是整体来看，单看局部点位是无法判断的，如下（仅凭下面三黑点两个红线是判断不出来的）：
在这里插入图片描述
判断方法，NetTopologySuite已提供，对于上图判断示例如下：

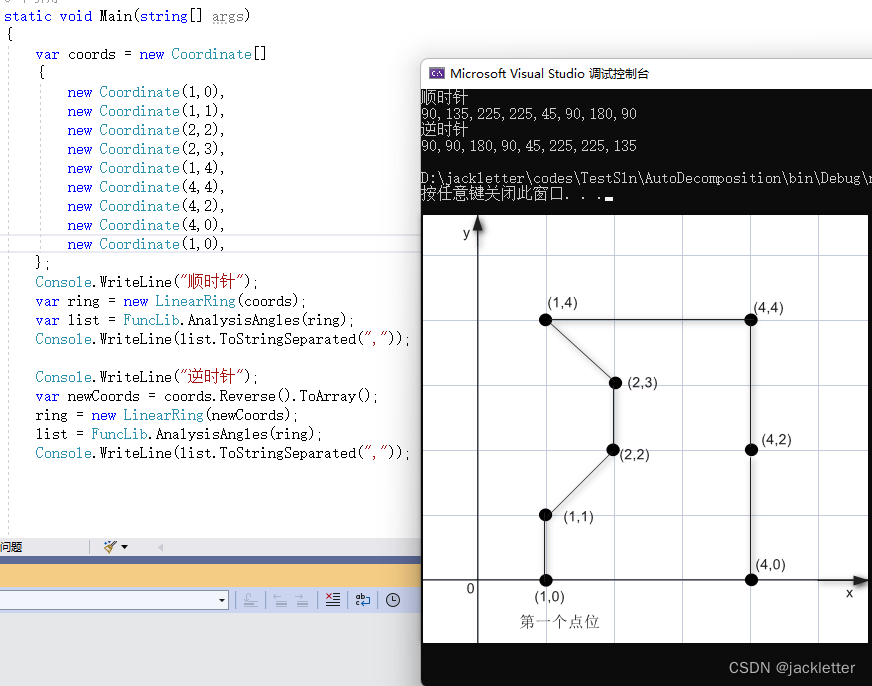
3.3 计算多边形的各个内角值（判断凹凸性）

计算内角，我们可以使用NetTopologySuite的方法：AngleBetweenOriented，这里我们需要按照点位顺序计算。
比如：p1、p2、p3、p4、p5
那么，计算点p2的内角为：∠p1p2p3，再结合多边形的方向（顺逆时针），将它转为(0,360)范围内。

下图为，顺逆时针和凹凸组合下的示意图：
在这里插入图片描述

由此可得计算的方法，如下：

public static class FuncLib
{public static List<double> AnalysisAngles(LinearRing ring){if (ring == null || !ring.IsSimple) throw new Exception($"数据错误!");var angels = new List<double>();for (int i = 0, len = ring.Coordinates.Length - 1; i < len; i++){var tail = ring[i];var t2 = ring[(i + 1) % len];var t1 = ring[(i - 1 + len) % len];var angle = AngleUtility.AngleBetweenOriented(t1, tail, t2);var angleDegree = AngleUtility.ToDegrees(angle);if (ring.IsCCW){//逆时针if (angle > 0){//concaveangleDegree = 360 - angleDegree;}else if (angle < 0){//convexangleDegree = -angleDegree;}else{//等于0 平行angleDegree = 180;}}else{//顺时针if (angle < 0){//concaveangleDegree = angleDegree + 360;}else if (angle > 0){//convex}else{//等于0 平行angleDegree = 180;}}angels.Add(angleDegree);}return angels;}
}