day52|● 300.最长递增子序列 ● 674. 最长连续递增序列 ● 718. 最长重复子数组
300.最长递增子序列
Input: nums = [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.
这题看似简单,但感觉没想明白递增的判定(当前下标i的递增子序列长度,其实和i之前的下表j的子序列长度有关系)和递推的关系
“子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序”。注意 这里是找递增子序列,他的递增可以是不连续的。
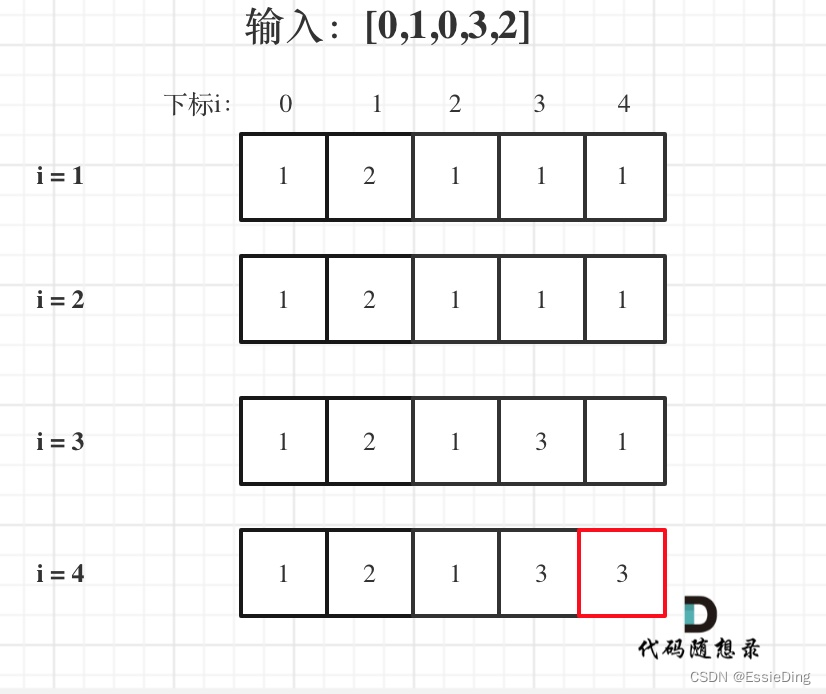
dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度
注意是以nums[i]结尾,和nums[j]比较(j在0到i之间),取最大的长度值
并非dp[i] 与 dp[j] + 1进行比较,而是我们要取dp[j] + 1的最大值。
需要把视角抽离出来,发现要求到当前i位置的最长递增子序列,其实依靠的是到他之前所有递增子序列长度的最大值,重点在[0 : i) 之前的所有dp
class Solution {public int lengthOfLIS(int[] nums) {// dp[i] the length of the longest increasing subsequence ending with nums[i]// dp[i]是以nums[i]为子序列尾元素的最长递增子序列的长度int[] dp = new int[nums.length];for (int i = 0; i < dp.length; i++) {dp[i] = 1;}int maxLength = 1;for (int i = 1; i < nums.length; i++) {for (int j = 0; j < i; j++) { // 着重注意理解这个forif (nums[i] > nums[j]){dp[i] = Math.max(dp[i], dp[j]+1);}}maxLength = dp[i] > maxLength ? dp[i]:maxLength;}return maxLength;}
}
时间复杂度: O(n^2)
空间复杂度: O(n)
674. 最长连续递增序列
dp[i]:以下标i为结尾的连续递增的子序列长度为dp[i]。
因为本题要求连续递增子序列,所以就只要比较nums[i]与nums[i - 1],而不用去比较nums[j]与nums[i] (j是在0到i之间遍历)。
既然不用j了,那么也不用两层for循环,本题一层for循环就行,比较nums[i] 和 nums[i - 1]。
class Solution {public int findLengthOfLCIS(int[] nums) {int[] dp = new int[nums.length];for (int i = 0; i < nums.length; i++) {dp[i] = 1;}int res = 1;for (int i = 1; i < nums.length; i++) {if (nums[i] > nums[i-1]) {dp[i] = dp[i-1]+1;}res = Math.max(res, dp[i]);}return res;}
}
时间复杂度:O(n)
空间复杂度:O(n)
718. 最长重复子数组
dp[i][j] :以下标i 为结尾的nums1,和以下标j 为结尾的nums2,最长重复子数组长度为dp[i][j]。
(特别注意: “以下标i 为结尾的A” 标明一定是 以A[i]为结尾的字符串 )
class Solution {public int findLength(int[] nums1, int[] nums2) {int[][] dp = new int[nums1.length][nums2.length];int maxLength = 0;for (int i = 0; i < nums1.length; i++) {for (int j = 0; j < nums2.length; j++) {if (nums1[i] == nums2[j]) {if (i==0 || j==0) {dp[i][j] = 1;} else {dp[i][j] = dp[i-1][j-1]+1;}}maxLength = Math.max(maxLength, dp[i][j]);}}return maxLength;}
}
