🎇🎇🎇作者：
@小鱼不会骑车
🎆🎆🎆专栏：
《数据结构》
🎓🎓🎓个人简介：
一名专科大一在读的小比特，努力学习编程是我唯一的出路😎😎😎

1. 优先级队列

1.1 概念

小鱼在之前的一篇博客中详细的介绍过队列,队列是一种先进先出(FIFO)的数据结构,但是有些情况下,操作的数据可能带有优先级,一般出队列时,可能需要优先级高的元素先出队列,例如我们在追剧时,如果是电池没电了,手机会优先提醒我们该充电了,而不是在等到你退出追剧的时候才弹出来,这时候就体现了优先级的重要性,包括打游戏时突然来电话,万一是很重要的电话,没有第一时间接到,是不是就可能产生很严重的后果!

在这种情况下,数据结构应该提高两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象.这种数据结构就是优先级队列(Priority Queue).

2. 优先级队列的模拟实现

JDK1.8中的PriorityQueue底层使用了堆这种数据结构,而堆实际就是在完全二叉树的基础上进行了一些调整.

2.1 堆的概念

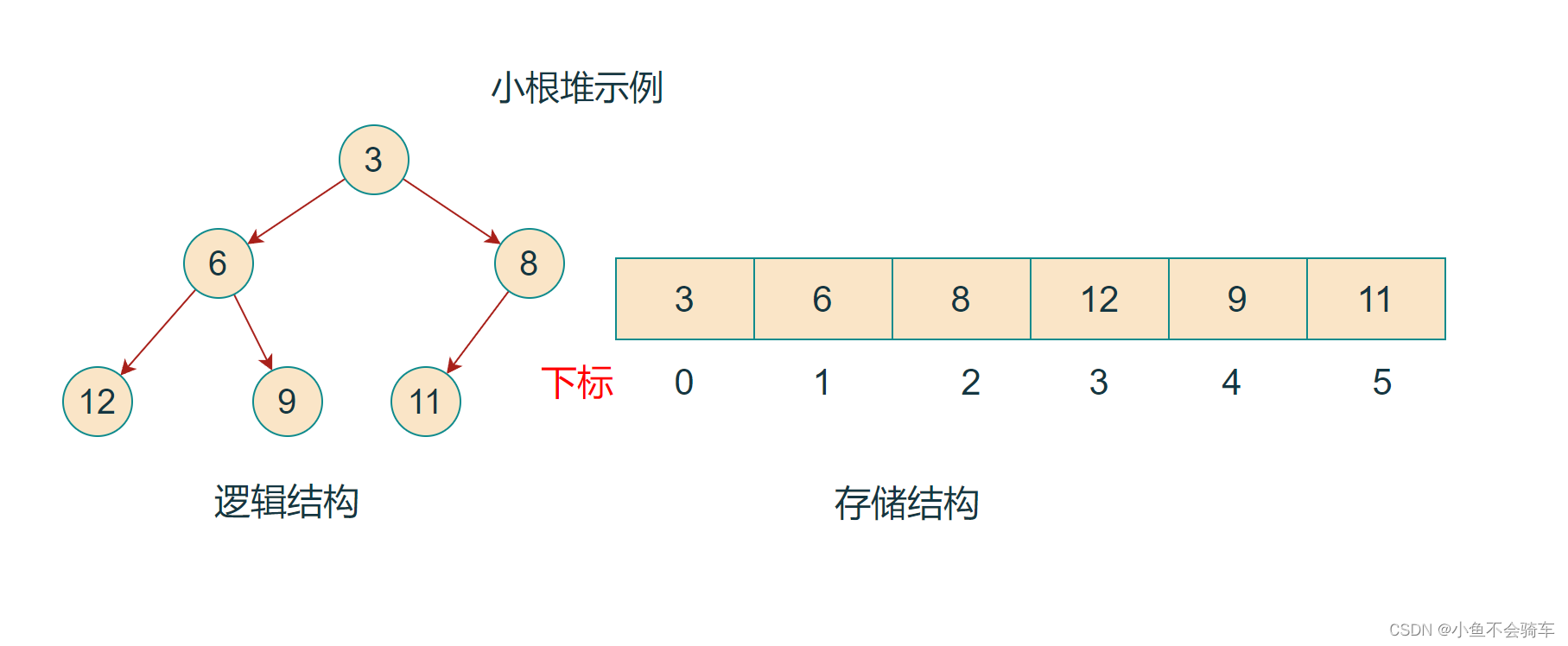
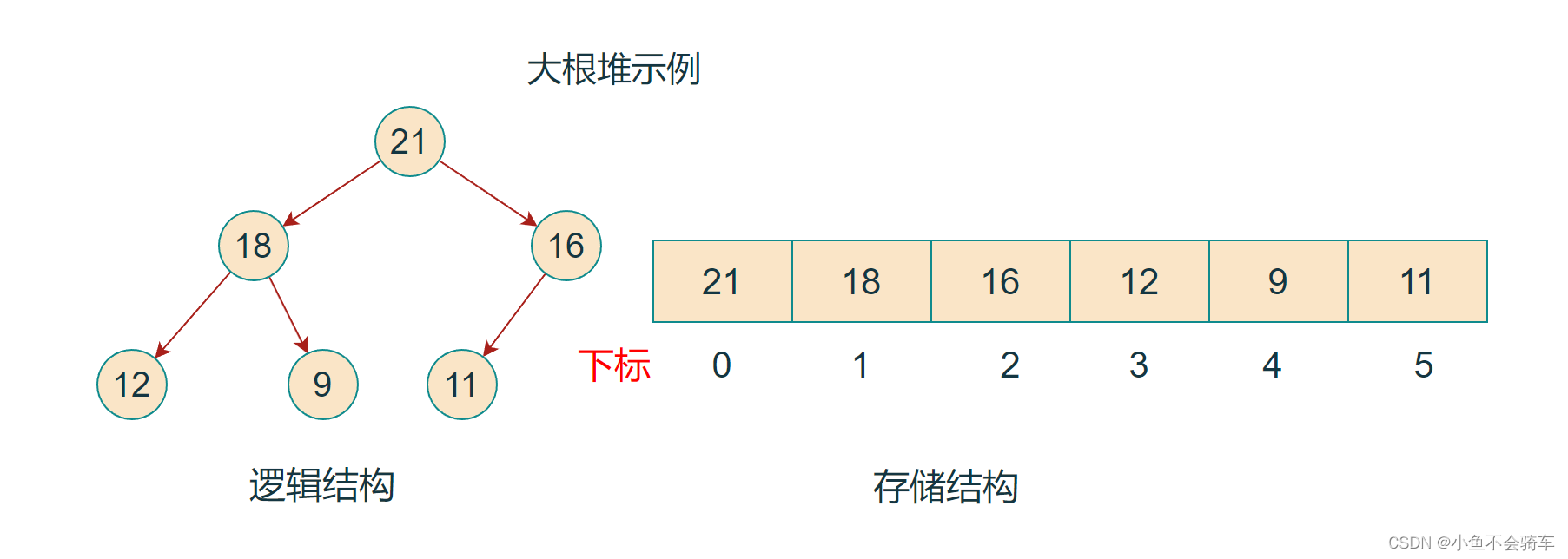
如果有一个关键码的集合K = {k0，k1， k2，…，kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中，并满足：Ki <= K2i+1 且 Ki<= K2i+2 (Ki >= K2i+1 且 Ki >= K2i+2) i = 0，1，2…，则称为 小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。

堆的性质：

• 堆中某个节点的值总是不大于或不小于其父节点的值；
• 堆总是一棵完全二叉树。

如下图:

2.2 堆的存储方式

从堆的概念可知,堆是一颗完全二叉树,因此可以按照层序遍历的规则采用顺序的方式来高效存储.

对于非完全二叉树实现的堆,如下图,该二叉树会造成空间上的浪费.

因此:对于非完全二叉树，则不适合使用顺序方式进行存储，因为为了能够还原二叉树，空间中必须要存储空节点，就会导致空间利用率比较低。

完全二叉树实现的堆如下图:

2.3 堆的创建

2.3.1 堆向下调整

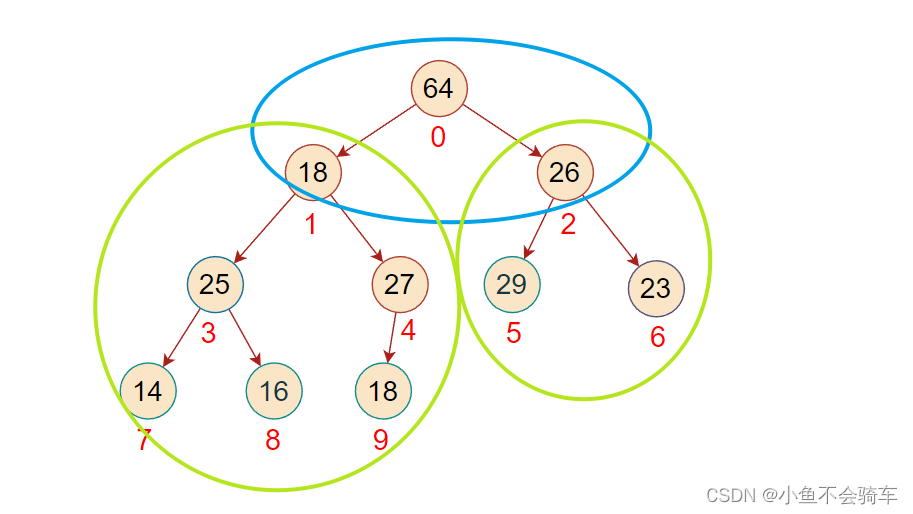
对于集合{ 23,25,64,35,18,29,33,14,16,27 }中的数据，如果将其创建成堆呢？

我们先把它的逻辑结构画出来!

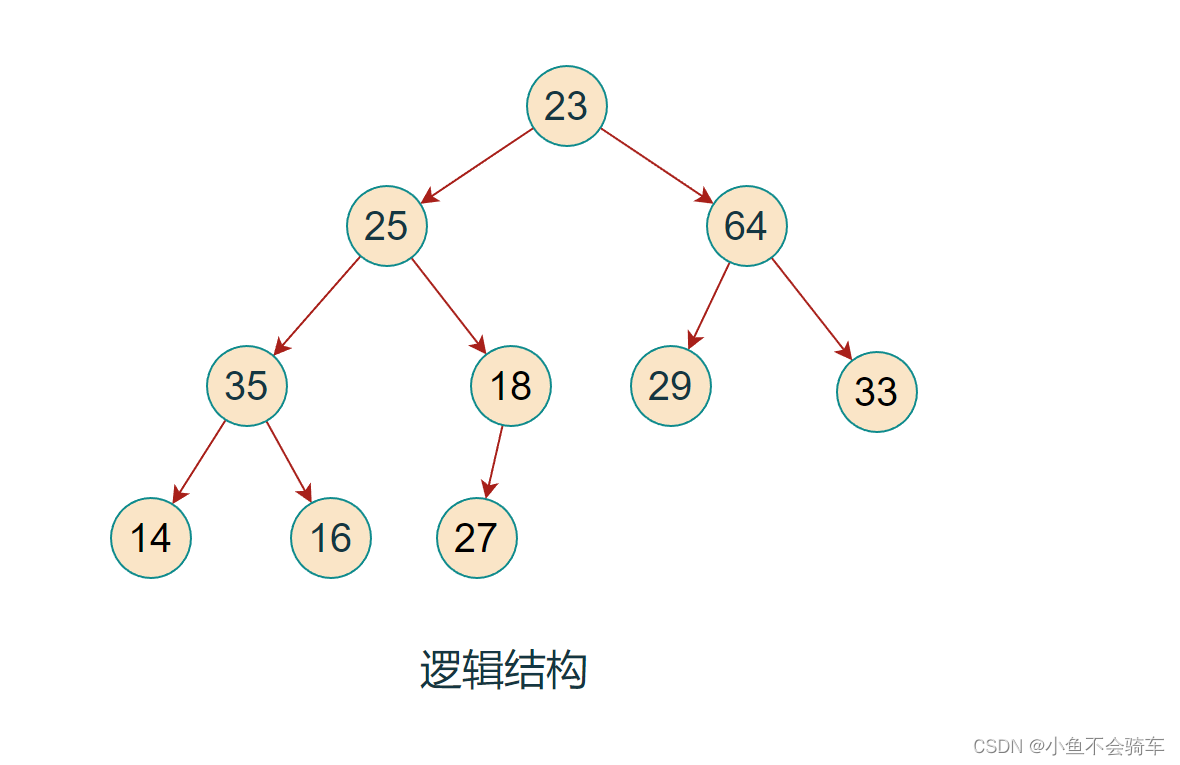
我们需要将该结构调整为大根堆.

大家先看过程,一边观看过程,一边理解思路.

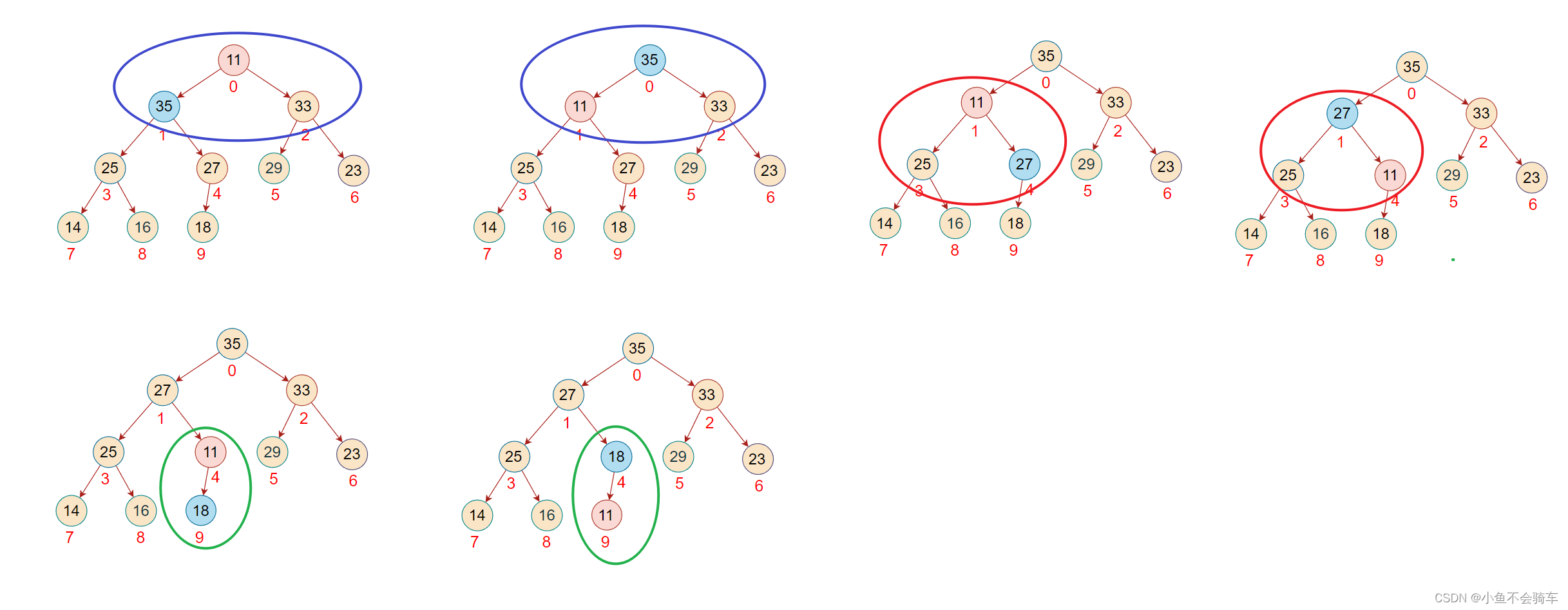
步骤一: 找到最后一颗含有孩子节点的树

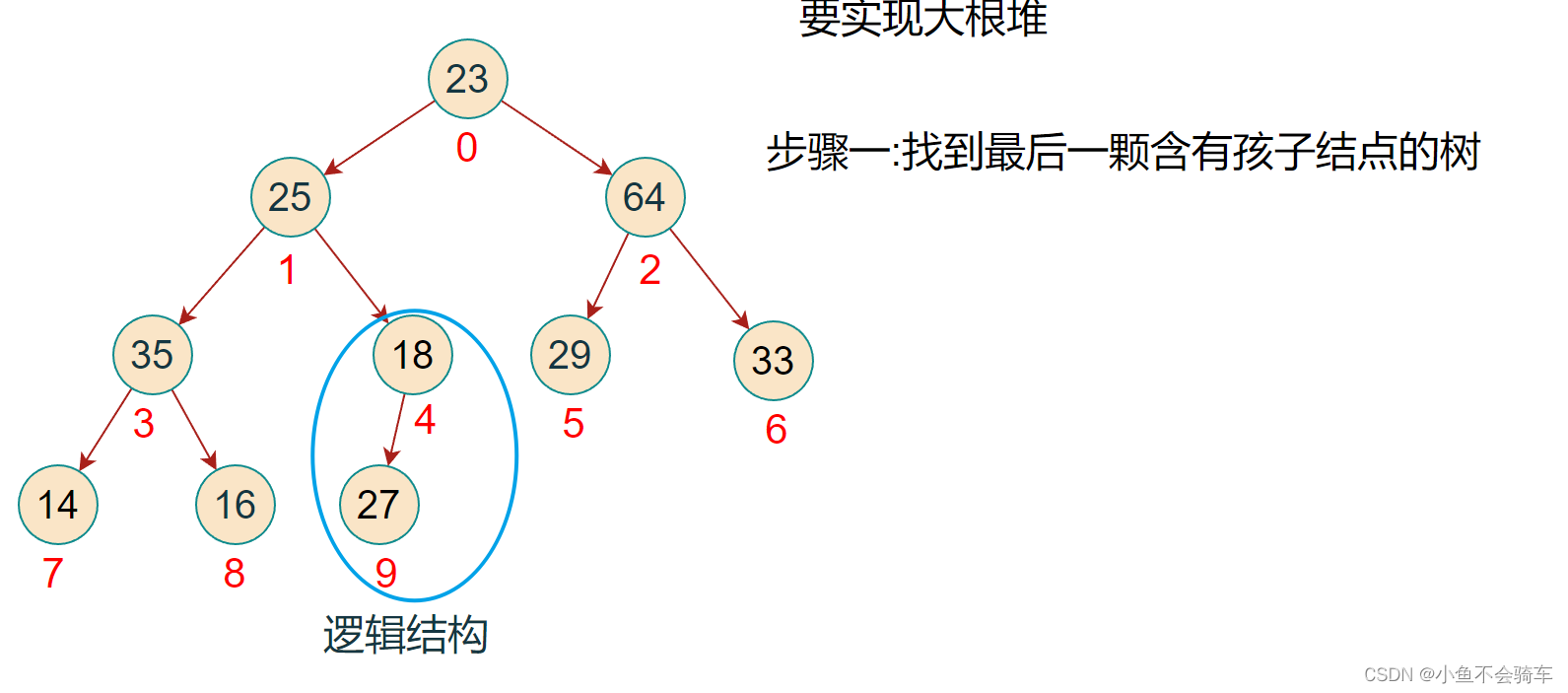
步骤二:

• 判断左右孩子结点是否存在
• 找出左右孩子节点的最大值(大根堆)
• 比较该子树的根节点也就是下标4对应的结点,判断下标为九的结点是否大于根节点
• 如果大于根节点,那就交换,如果小于则不进行交换

步骤三:由于大于子树的根节点,那么进行交换

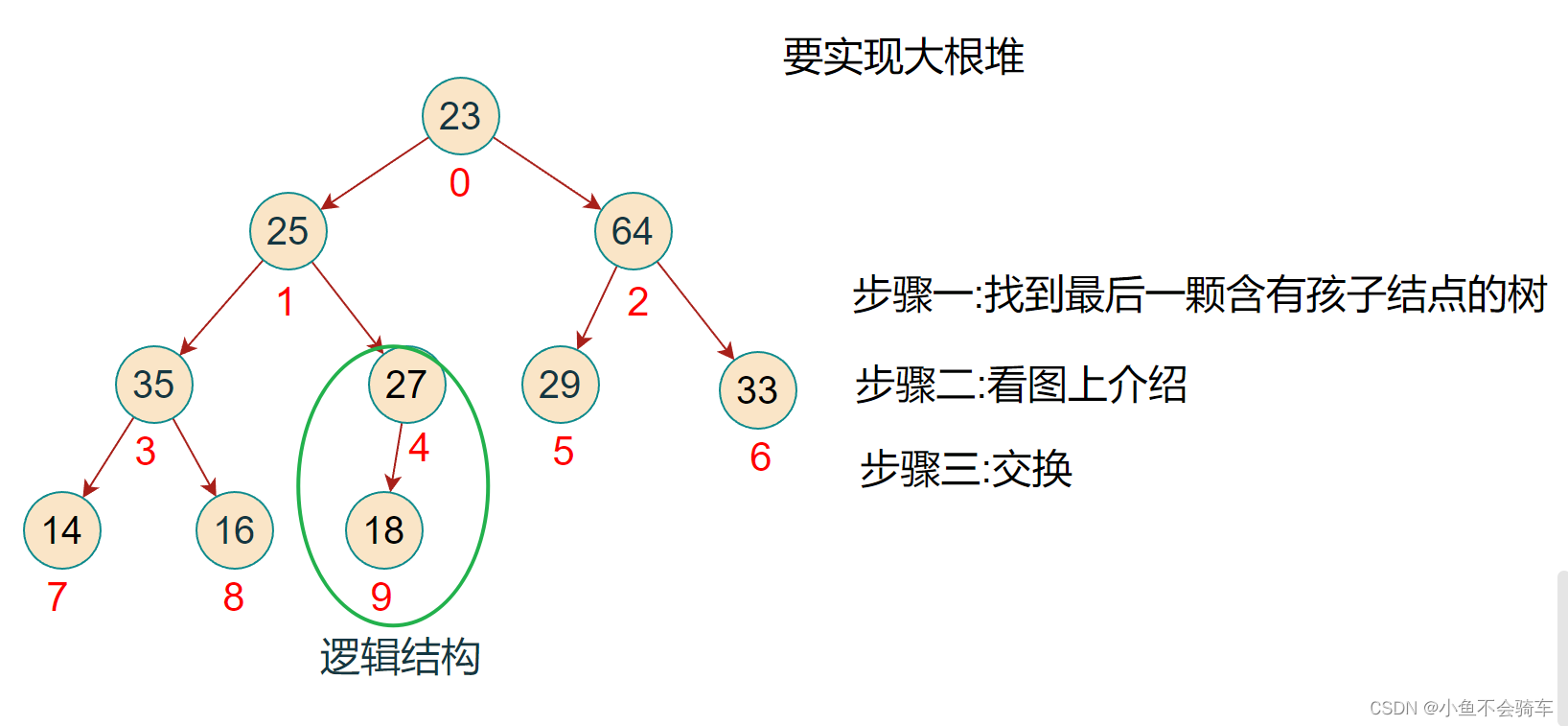
步骤四:下标为4的这个结点对应的子树已经是大根堆了,下一步对下标为3的这个结点,将该树改为大根堆

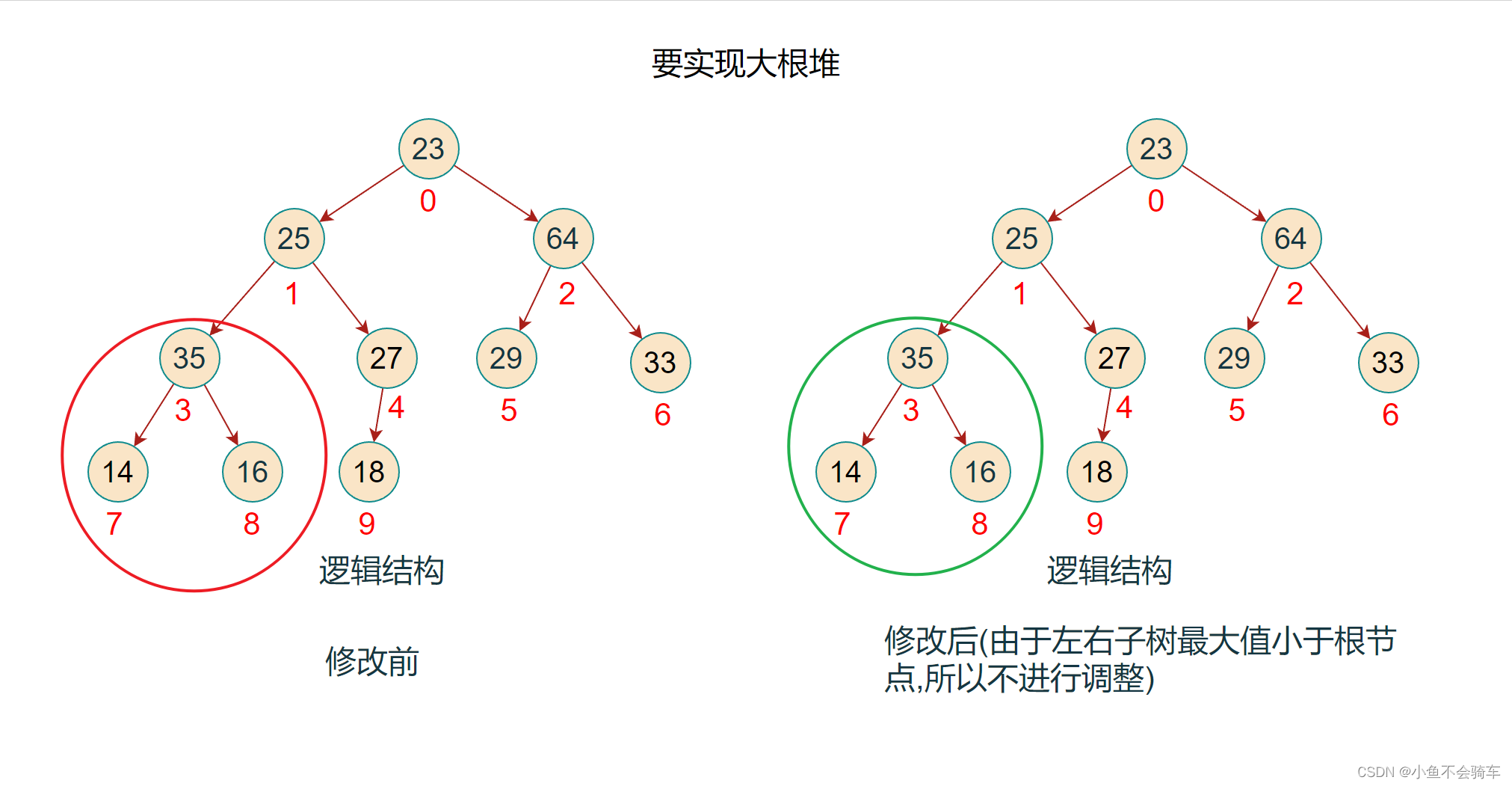
步骤五:重复步骤二,将下标为2的结点对应的子树调整为大根堆

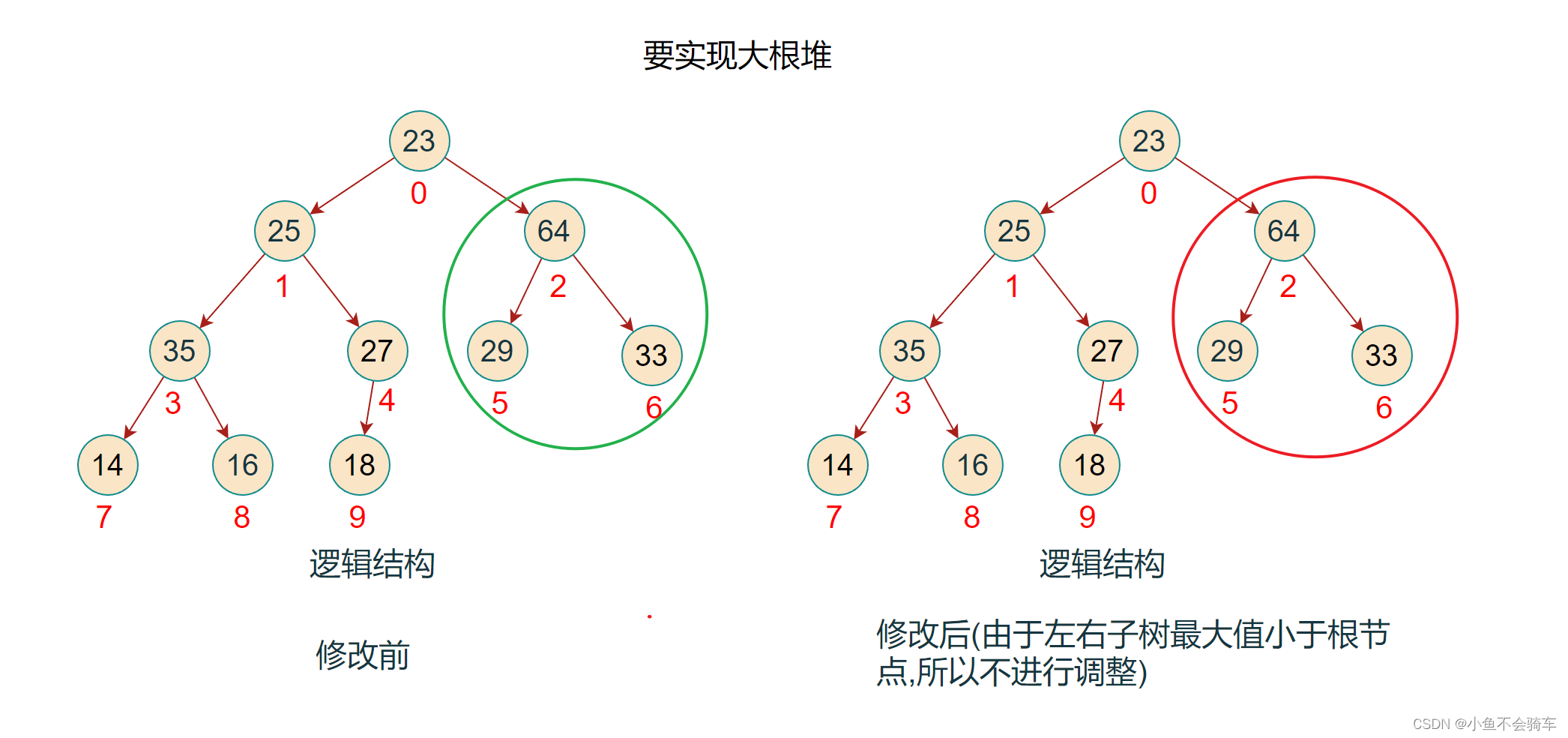
步骤六:对下标为1的结点所对应的树进行调整,依旧是重复上述操作

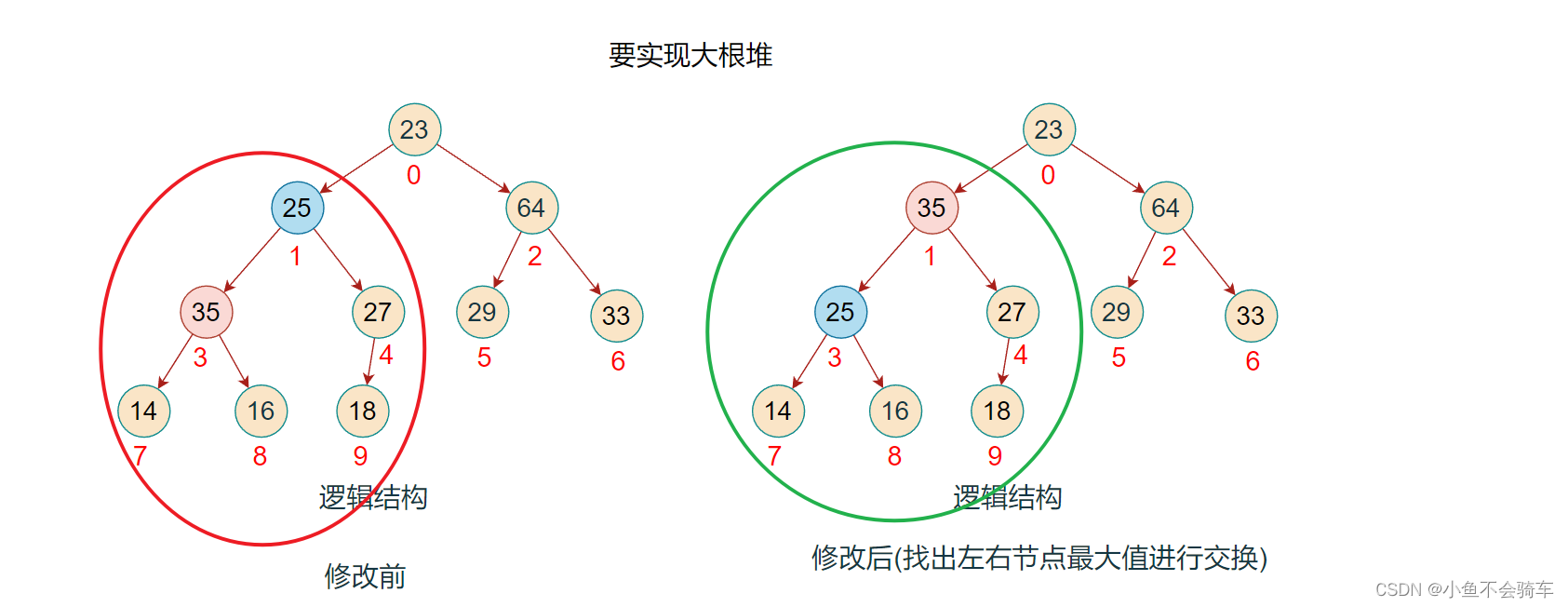
步骤七:此时该子树并没有调整完,需要注意!!!由于下标为1的结点和下标为3的结点进行了交换,那么还需要进行一步操作就是判断,被交换值的下标为3的结点是否是下标为3的节点所对应的这颗树中的最大值!

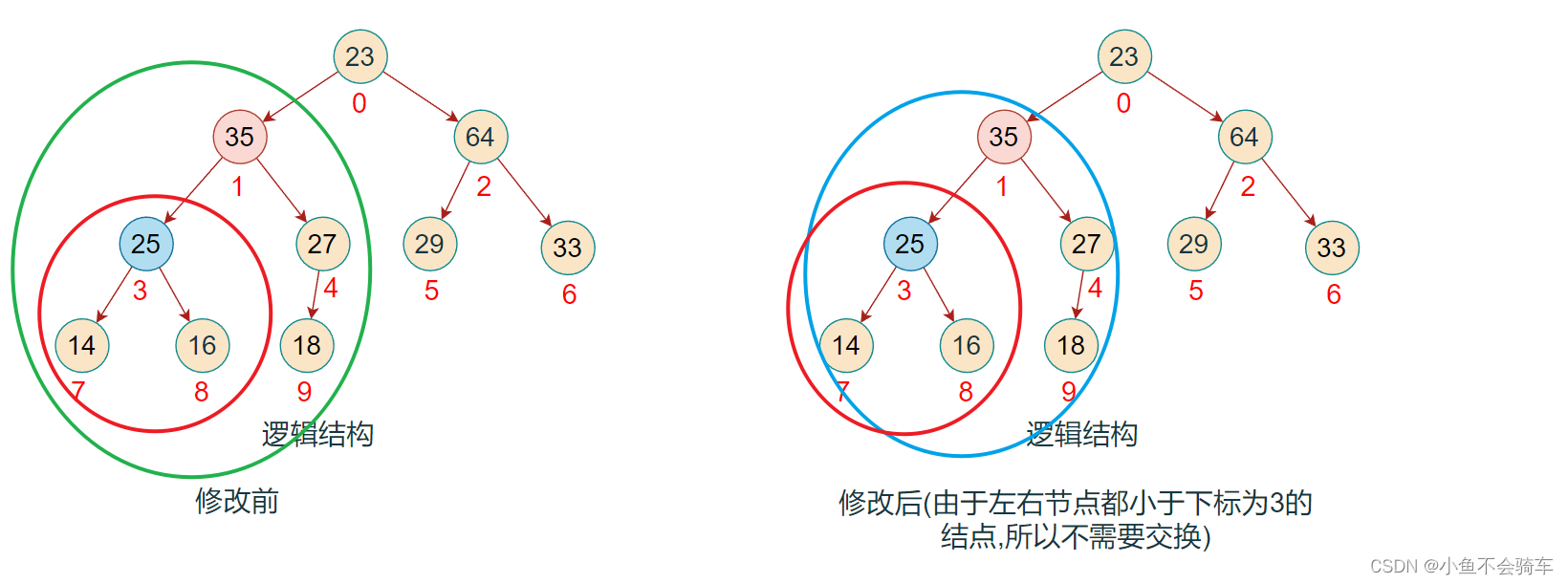
步骤八:现在对下标为0的结点进行调整(下标为2和下标为0的结点进行了交换),红色框对应的是该结点所对应的树,绿色的框是正在进行比较的树

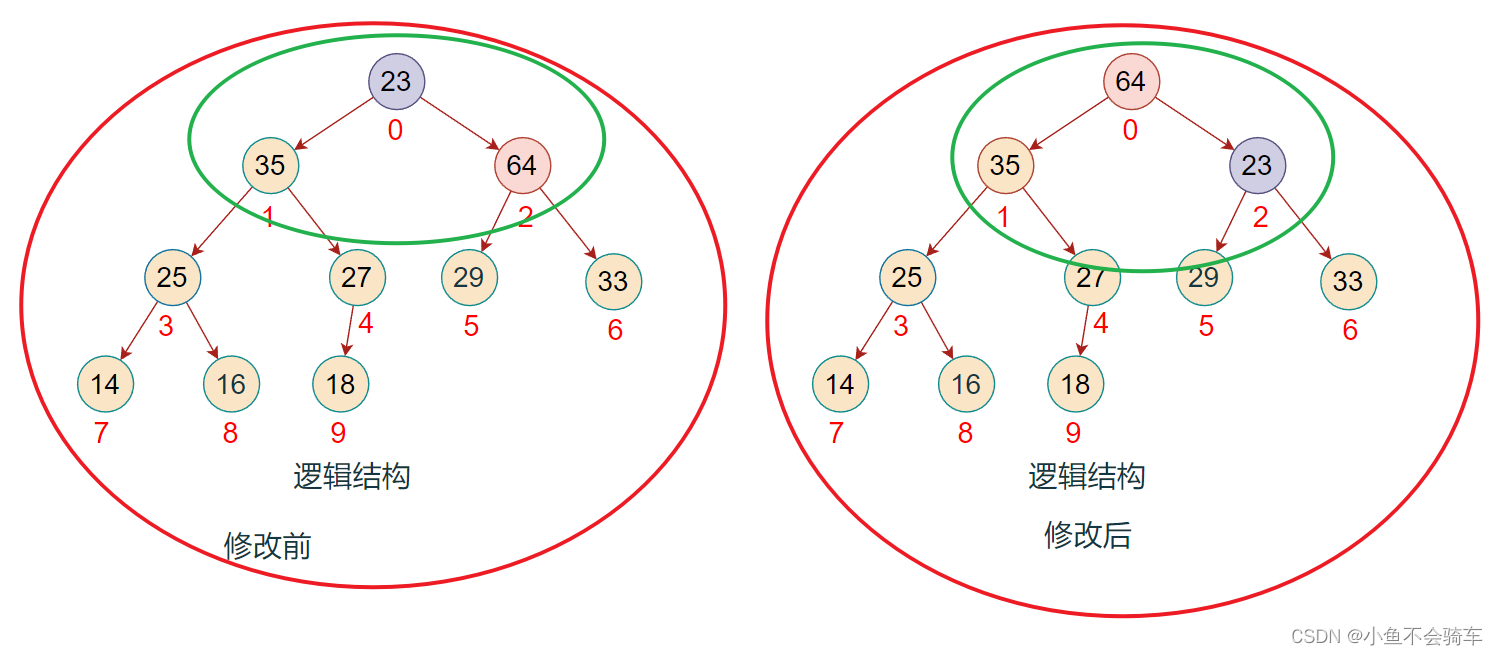
步骤九:由于前面进行了交换,将下标为2的值进行了修改,此时并不能确认下标为2所对应的树是否还是大根堆,所以需要重复步骤二的操作,也就是找出左右孩子结点的最大值进行比较.

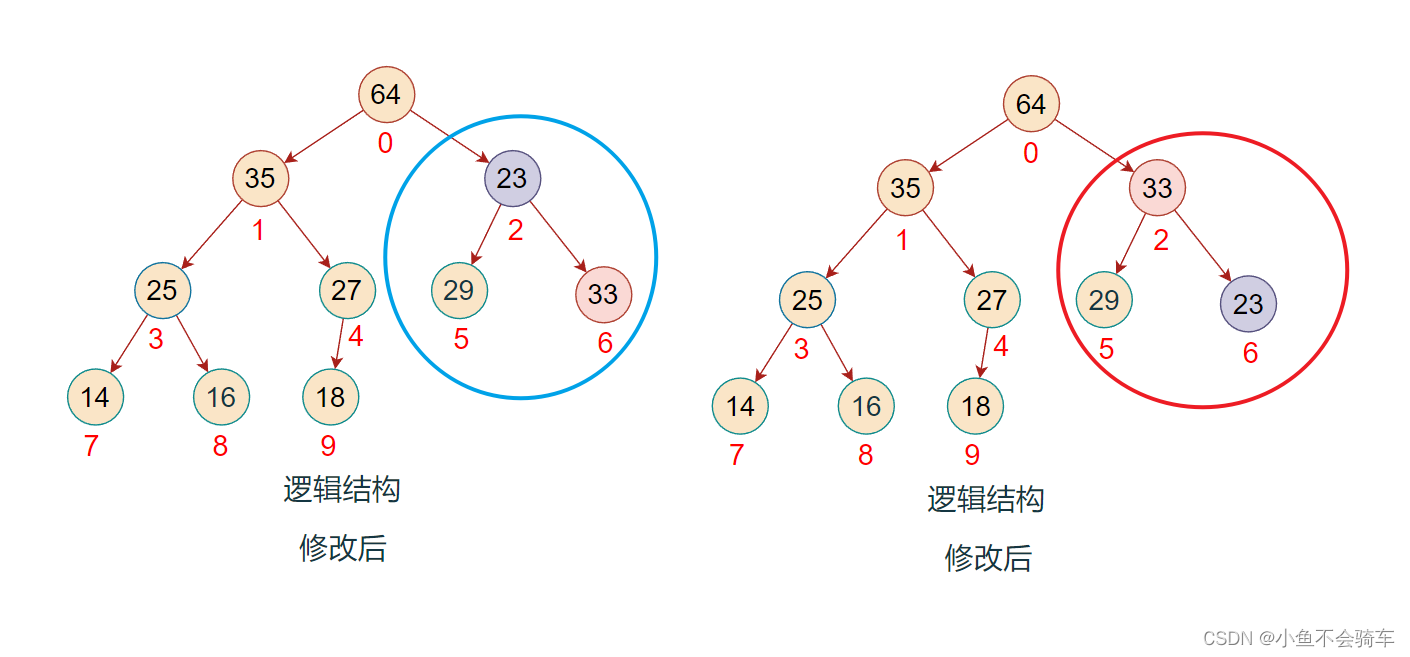
此时,该完全二叉树也就变成了一个大根堆,任何一颗子树的根节点都大于它的任何一个孩子节点.

如下图(每一个框框所对应的树的根节点都大于它的孩子结点):

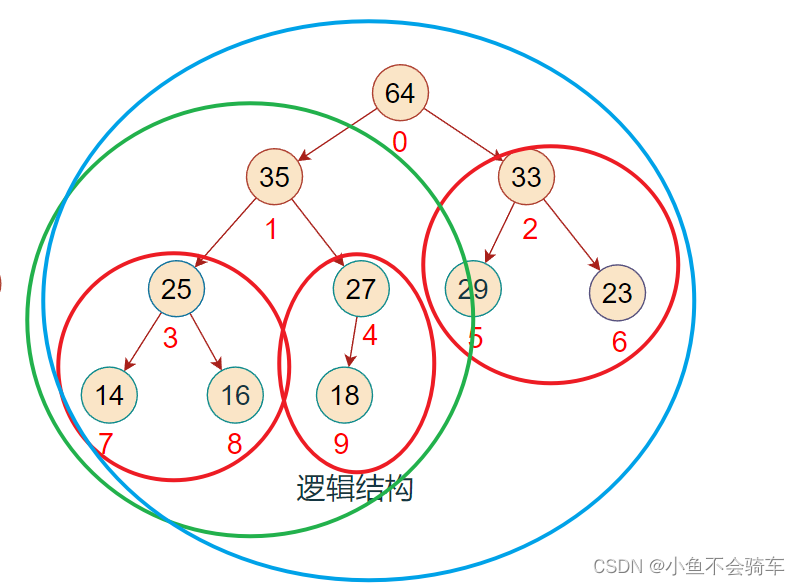
上述的操作我们称之为向下调整.

此时我们再去观看下面的过程是不是更容易理解.

向下过程(以大堆为例)：

1. 让parent标记需要调整的节点，child标记parent的左孩子(注意：parent如果有孩子一定先是有左孩子)
2. 如果parent的左孩子存在，即:child < size， 进行以下操作，直到parent的左孩子不存在:

• parent右孩子是否存在，存在找到左右孩子中最大的孩子，让child指向左右孩子最大值所对应的下标.
• 将parent与较大的孩子child比较，如果：

• parent大于较小的孩子child，调整结束
• 否则：交换parent与较大的孩子child，交换完成之后，parent中小的元素向下移动，可能导致子树不满足对的性质，因此需要继续向下调整，即parent = child；child=parent*2+1; 然后继续2的操作。

难点1:其实对于这道题的难点,就是找向下调整的边界,什么时候停止调整呢?
难点2:为什么要从最后一颗含有子节点的树开始向下调整.

讲解难点一:首先我们要知道,如果想要进行向下调整那么需要最基本的条件就是它有孩子结点,也就是至少存在左孩子,如果左孩子都不存在,那么该节点就不需要进行调整,此时问题就变成了,如何判断左孩子是否存在!

我们看下图:

下标为4的结点是有孩子结点的,孩子结点的下标是9,在二叉树中我们学过,给父亲节点下标,求左右孩子结点的下标,根据公式(求左孩子下标)child = parent * 2 +1.那么它是否有右孩子结点呢?我们看图片可以很清楚的看到他是没有右孩子结点的,我们假设它有右孩子结点,我们求出右孩子结点的下标:4*2+2 = 10,此时右孩子结点的下标为10,但是我们回归该图,该图只有十个结点,又因为下标是从0开始的,那么下标值最高为9,此时右孩子下标是10,说明以及越界了,并不包含右孩子,此时我们就可以找到这个边界,也就是child < 二叉树结点的个数,为了证明该判断的合理性我们试求下标5的孩子节点是否存在,答案是不存在( 5 * 2 + 1 = 11 11 > 二叉树结点的个数,不符合条件),下标6也如此,都是不存在孩子结点的.

讲解难点2:为什么要从最后一个含有子节点的树进行向下调整?

我们先举个反例:

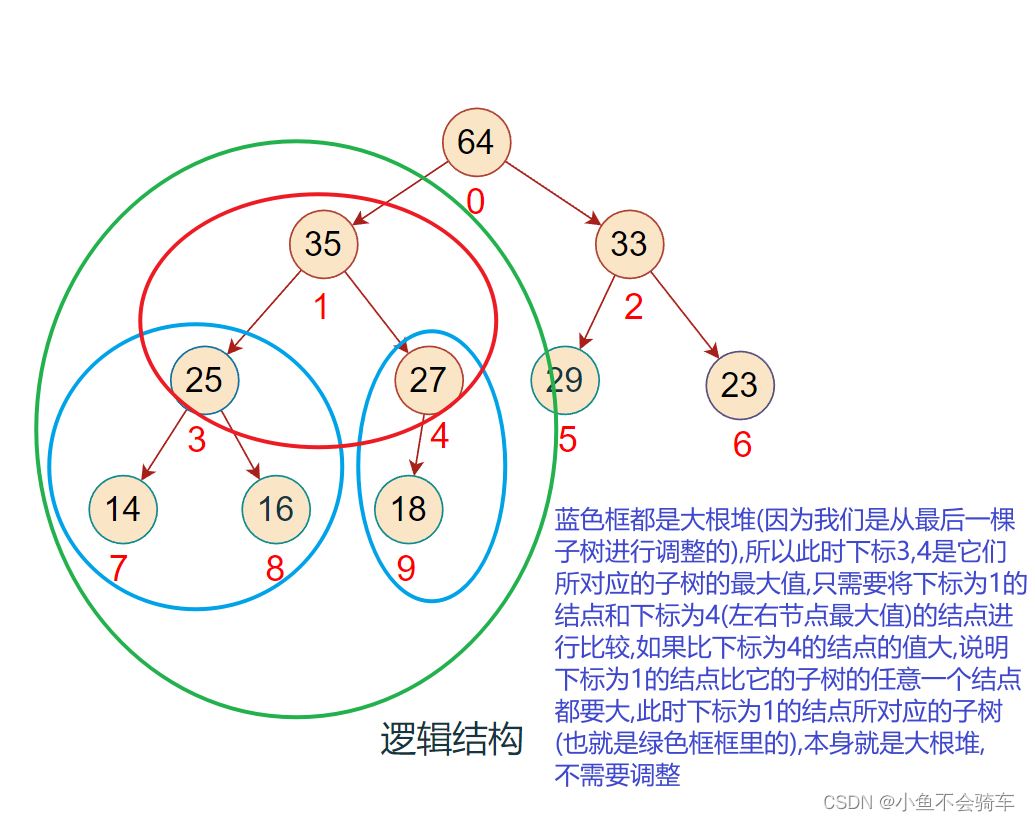
若我们只对0下标对应的结点进行向下调整,大家看上图,此时左右子树都小于根节点,所以不再进行向下调整,但是可以看到,绿色框框里面的树还并不是大根堆,所以从0开始调整是有可能会出错的!

由于我们是从最后一颗子树进行调整的,那么假如我们调整到了下标为1的结点所对应的子树,我们可以保证,比下标1大的下标(例如2,3,4…)所对应的结点的子树一定是大根堆, 而且我们还可以得到一个信息就是:

代码如下:

   public void createHeap(){//从最后一个结点的父亲结点开始向下调整for (int parent = (UsedSize-1-1)/2; parent >=0 ; parent--) {//UsedSize就是结束条件,也就是节点个数shiftDown(parent,UsedSize);}}/*** 父亲下标和每棵树的结束下标* @param parent*///大根堆private void shiftDown(int parent,int len) {//接受了父亲节点//求出子节点下标int child=2*parent+1;//判断孩子节点下标是否越界while (child<len) {//判断右节点是否存在,如果存在找出左右节点最大值(顺序不能颠倒)if(child+1<len && elem[child]<elem[child+1]) {child++;}//子节点大于父亲节点就交换if(elem[child]>elem[parent]) {swap(elem,parent,child);//此时的父亲节点指向被修改后的子节点parent=child;//子节点依旧是该父亲结点所对应的左孩子结点child=2*parent+1;}else {//如果没有交换就直接退出break;}}}private void swap(int[]array,int left,int right) {int tmp=array[left];array[left]=array[right];array[right]=tmp;}

我们来算一下向下调整的时间复杂度,大家看下图:

时间复杂度分析：
最坏的情况即图示的情况，从根一路比较到叶子，比较的次数为完全二叉树的高度，即时间复杂度为O(logN)

2.3.2 建堆的时间复杂度

我们按照最坏情况考虑,也就是每个结点都需要进行调整,并且每个结点调整的高度都是它所在层数到叶子层数的距离.

则需要移动总的步数为:

T(n) = 2 ^ 0 * ( h - 1 ) + 2 ^ 1*(h - 2) + 2 ^ 2 * ( h - 3) + 2 ^ 3 ( h - 4 ) +…+ 2 ^ ( h - 3 ) * 2 + 2 ^ ( h - 2 ) * 1 ①
2 * T(n) = 2 ^ 1 * ( h - 1 ) + 2 ^ 2(h - 2) + 2 ^ 3 * ( h - 3) + 2 ^ 4 ( h - 4 ) *+…+ 2 ^ ( h - 2 ) * 2 + 2 ^ ( h - 1 ) * 1 ②
② - ① 错位相减:

T(n) = 1 - h + 2 ^ 1 + 2 ^ 2 + 2 ^ 3 + 2 ^ 4 +…+2(h-2)+2^(h-1)
T(n) = 2 ^ 0 + 2 ^ 1 + 2 ^ 2 + 2 ^ 3 + 2 ^ 4 +…+2(h-2)+2^(h-1) - h
T(n) = 2 ^ h - 1 - h
n = 2 ^ h -1
h = log(n+1)
T(n) = n - log(n+1) ≈ n

因此:建堆的时间复杂度为O(N)

2.3.3 堆的向上调整

刚才讲完了向下调整,那么这次我们讲解一下什么是向上调整.

向上调整一般使用的范围是在建堆的时候,还有插入结点的时候.

插入举例:

向上调整需要一个前提,就是当前的堆需要是大根堆(小根堆),我们以大根堆举例:

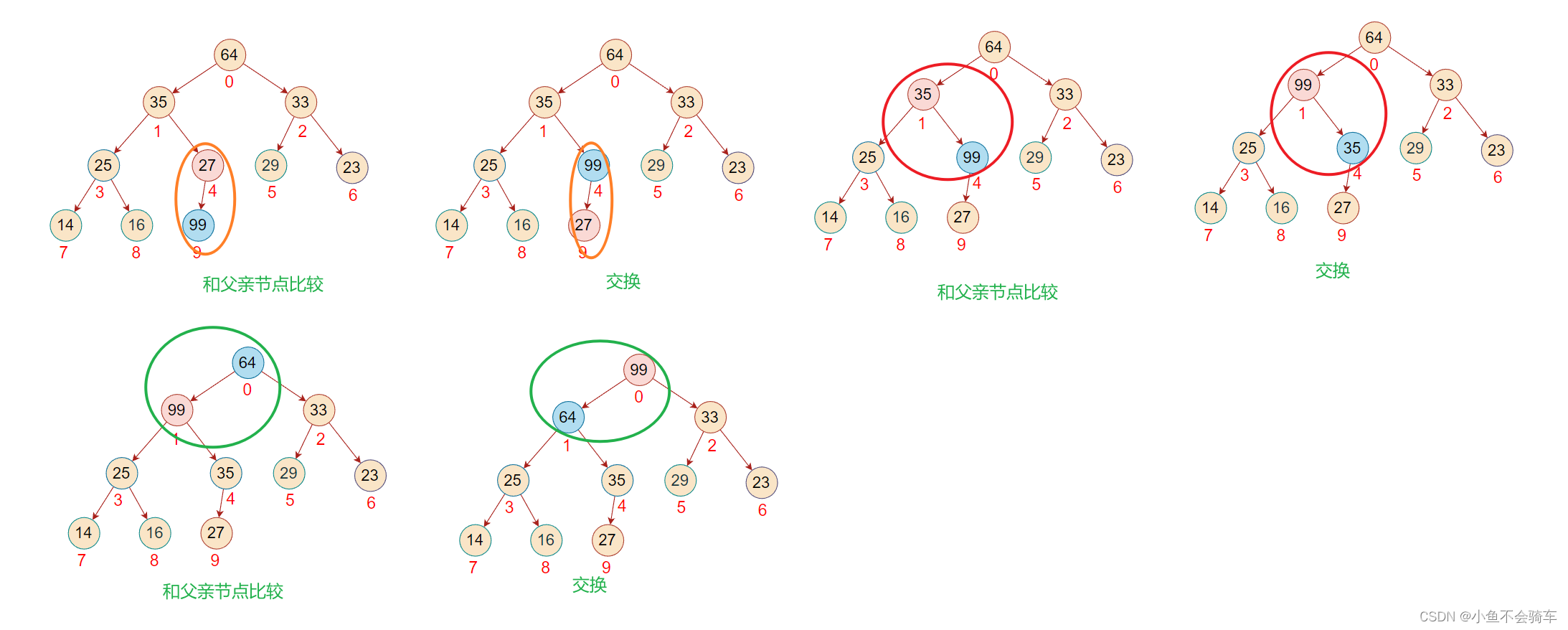
假如99这个结点是新插入的,需要将该树的结构重新改为大根堆,那么需要进行向上调整,具体过程就是:

99和它的父亲节点,也就是下标为4的结点进行比较,如果比父亲节点大,那就交换,此时就跟上述图片的第二步一样,再去用99的结点和它当前的父亲节点进行比较(也就是下标为1的结点),如果比父亲结点大,那就交换,重复上述操作.

问题:不需要左右孩子结点比较吗?

答案:不需要,因为在插入之前,该树就是一个大根堆.

我们用红色框框里面的内容举例:在没有插入99这个结点时,下标为1的结点比下标为3,4结点的值都要大,所以我们可以知道,即使我们的99和下标为4的元素交换,由于下标为3的结点并没有改变,所以我们下标为1的结点还是比下标为3的结点大的,所以就不需要用新的下标为4的结点和下标为3的结点进行比较了.只需要和它的父亲节点进行比较就行.

代码入下:

    //插入、public void offer(int val) {//判满if(isFUll()) {elem= Arrays.copyOf(elem,elem.length*2);}//末尾添加新元素然后UsedSize++//UsedSize是记录数组长度的elem[UsedSize++]=val;//进行向上调整,传入最后一个叶子结点shiftUp(UsedSize-1);}//向上调整public void shiftUp(int child) {//找到该结点的父亲结点int parent = (child-1)/2;//边界就是孩子结点不能为0,如果孩子结点为0说明不需要调整了while (child != 0) {//不需要左右孩子结点进行比较,因为该孩子节点的另一个兄弟结点一定小于父亲节点//子节点大于父亲节点就交换if(elem[child] > elem[parent]) {swap(elem,child,parent);}else {//如果不大于那就直接退出break;}//不断地进行向上调整,//可以对照上述画的图片进行理解child = parent;parent = (parent-1)/2;}}

时间复杂度:最坏的情况即图示的情况，从叶子一路比较到根，比较的次数为完全二叉树的高度，即时间复杂度为O(logN)

建堆举例:

大家看图:

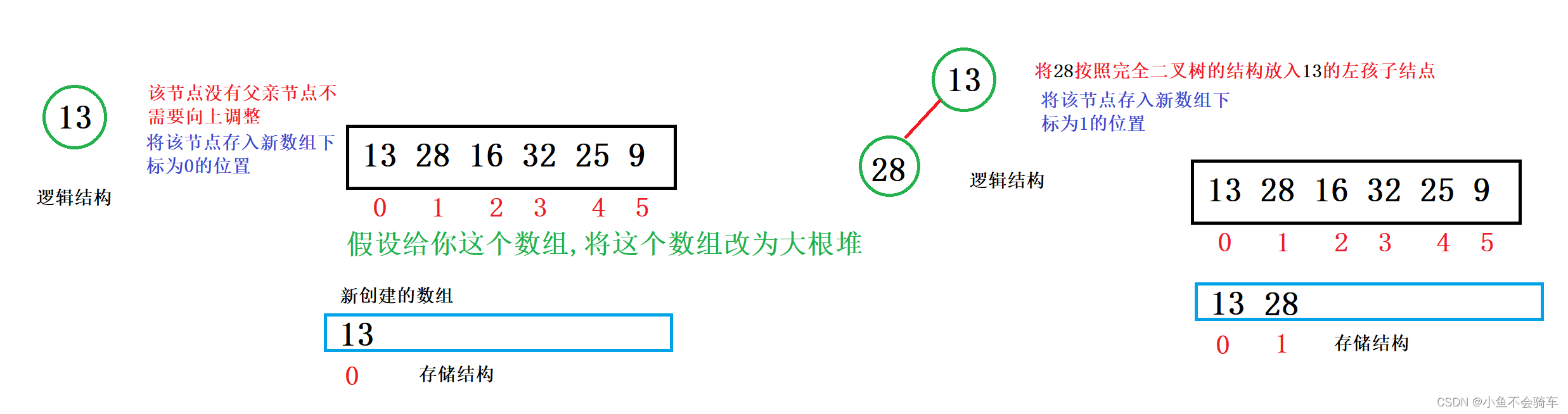
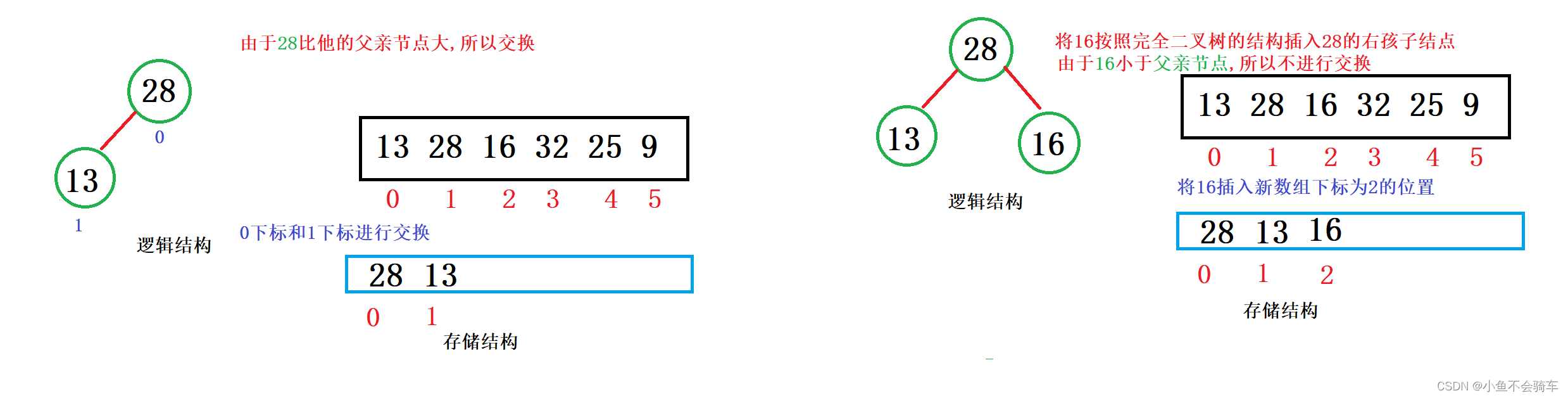
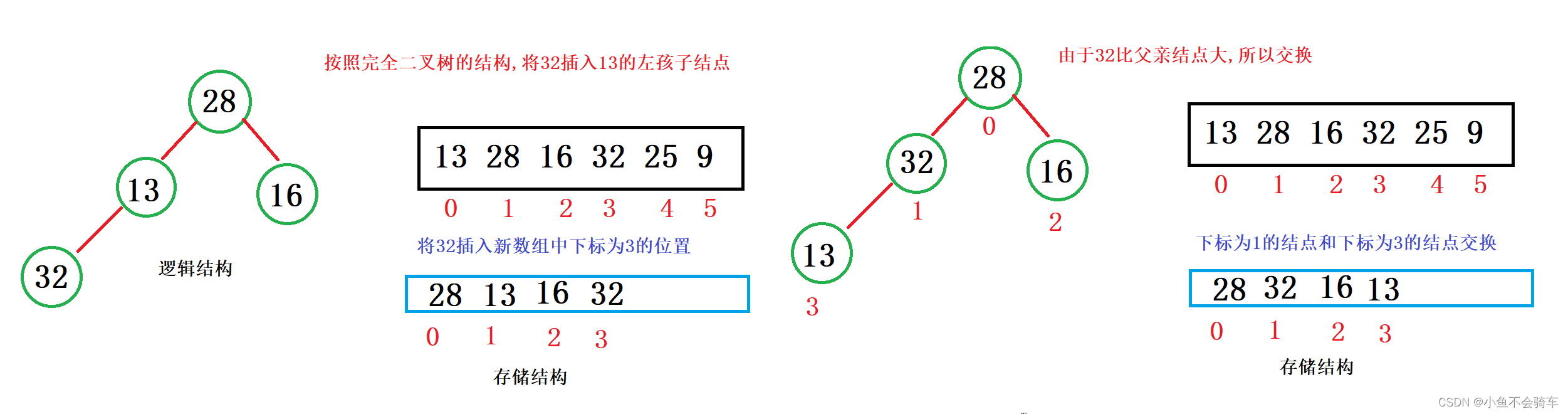
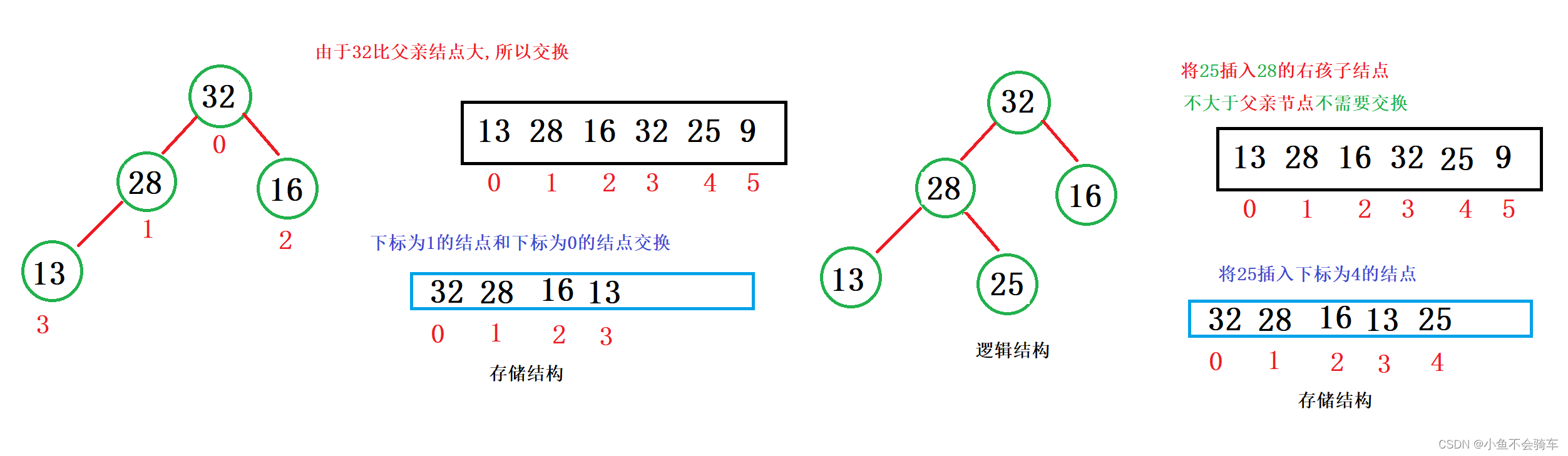
通过上述的过程,我们就通过向上调整建好了一个大根堆.

代码入下:

  //建堆public void createHeap(int[] array){for (int i = 0; i < array.length ; i++) {offer(array[i]);}}//插入、public void offer(int val) {//判满if(isFUll()) {elem= Arrays.copyOf(elem,elem.length*2);}//尾插要新增的结点elem[UsedSize++]=val;//将新插入的结点进行向上调整shiftUp(UsedSize-1);}//向上调整public void shiftUp(int child) {int parent = (child-1)/2;while (child != 0) {//子节点大于父亲节点if(elem[child] > elem[parent]) {swap(elem,child,parent);}else {break;}//子节点 = 父节点child = parent;//父节点 = 父节点的父节点parent = (parent-1)/2;}}//交换private void swap(int[]array,int left,int right) {int tmp=array[left];array[left]=array[right];array[right]=tmp;}

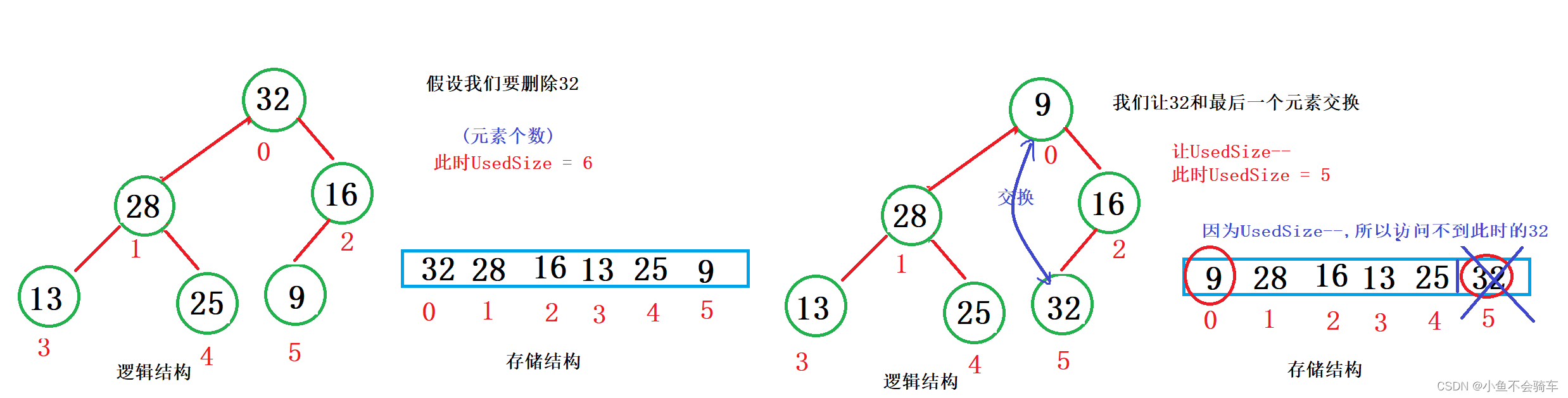
2.3.4 堆的删除

由于删除的是堆顶元素,我们思考一下,如何删除?有人会想到:将堆顶元素删除,然后所有元素向前移一位,最后再对每个结点进行向下调整.其实这个方法是行得通的,但却不是一个好的方法,因为所有元素前移一位就会打乱堆本身的顺序,再对堆中的每个元素向下调整,那么时间复杂度最坏可以达到O(N),那有没有什么好一些的方法吗?

答案是:有的.

注意：堆的删除一定删除的是堆顶元素。具体如下：

1. 将堆顶元素对堆中最后一个元素交换
2. 将堆中有效数据个数减少一个
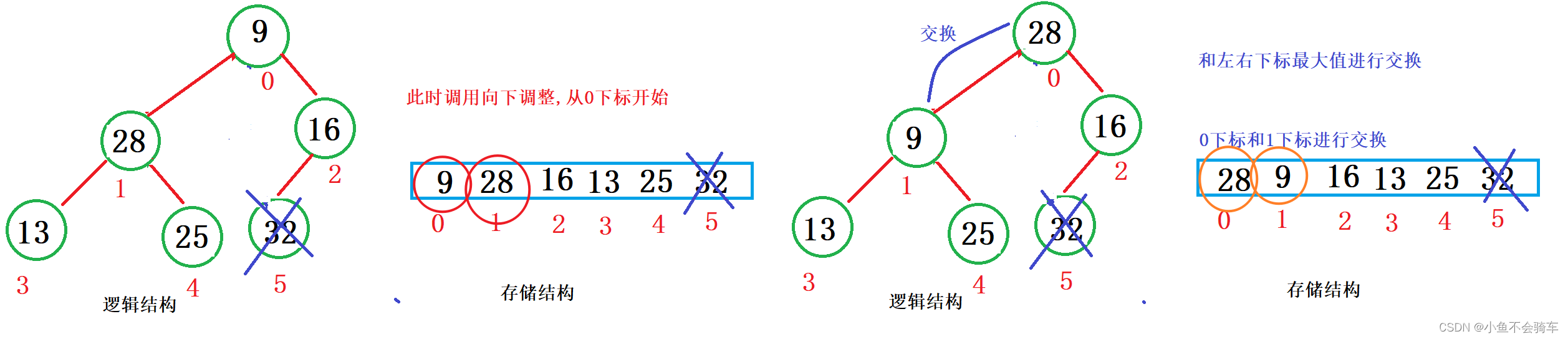
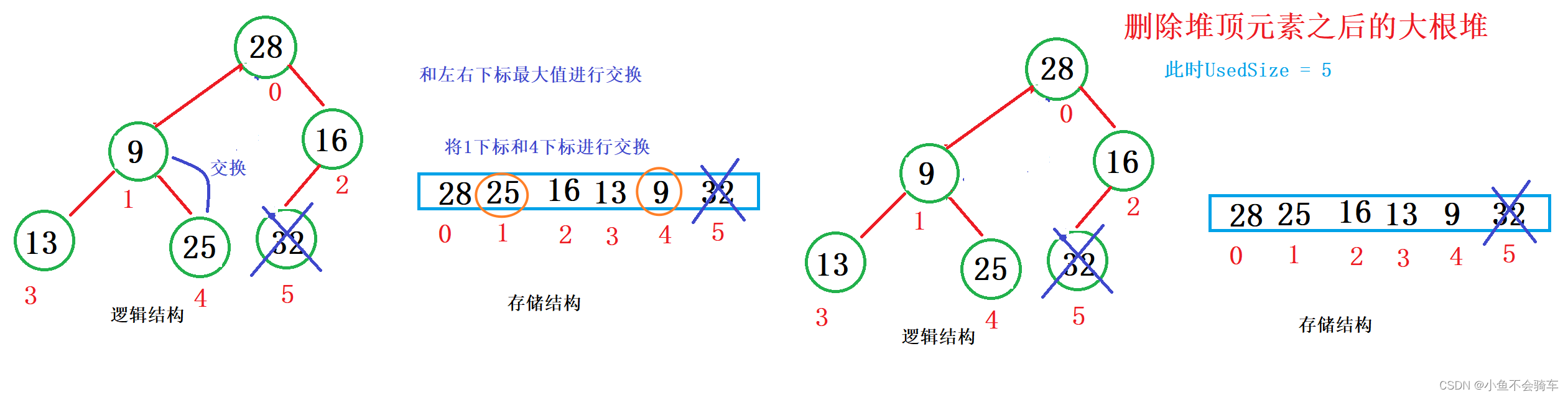
3. 对堆顶元素进行向下调整

我们看图:

代码入下:

    /*** 删除* @return*/public int pop() {if(isEmpty()) {return -1;}int tmp = elem[0];//交换swap(elem,0,UsedSize-1);//元素个数-1UsedSize--;//调用向下调整,从0开始shiftDown(0,UsedSize);return tmp;}

时间复杂度 : O(logN) 即树的高度