当前位置：首页 > news >正文

(树) 剑指 Offer 07. 重建二叉树 ——【Leetcode每日一题】

news 2025/7/22 17:46:26

❓剑指 Offer 07. 重建二叉树

难度：中等

输入某二叉树的 前序遍历 和 中序遍历 的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例 1:

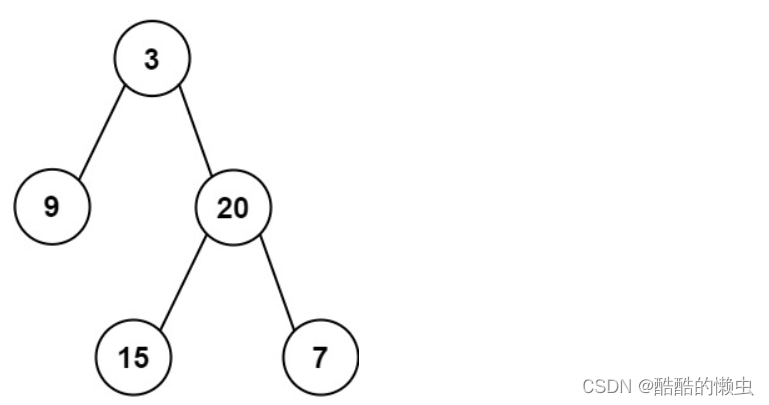
在这里插入图片描述
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

限制：

0 <= 节点个数 <= 5000

注意：本题与 105. 从前序与中序遍历序列构造二叉树相同。

💡思路：递归

二叉树前序遍历的顺序为：

先遍历根节点；
- 随后递归地遍历左子树
- 最后递归地遍历右子树

二叉树中序遍历的顺序为：

先递归地遍历左子树；
随后遍历根节点；
最后递归地遍历右子树

在「递归」地遍历某个子树的过程中，我们也是将这颗子树看成一颗全新的树，按照上述的顺序进行遍历。挖掘「前序遍历」和「中序遍历」的性质，我们就可以得出本题的做法。

前序遍历的第一个值为根节点的值，使用这个值将 中序遍历 结果分成两部分：

左部分 为树的左子树中序遍历结果；
右部分 为树的右子树中序遍历的结果；
然后分别对左右子树递归地求解。

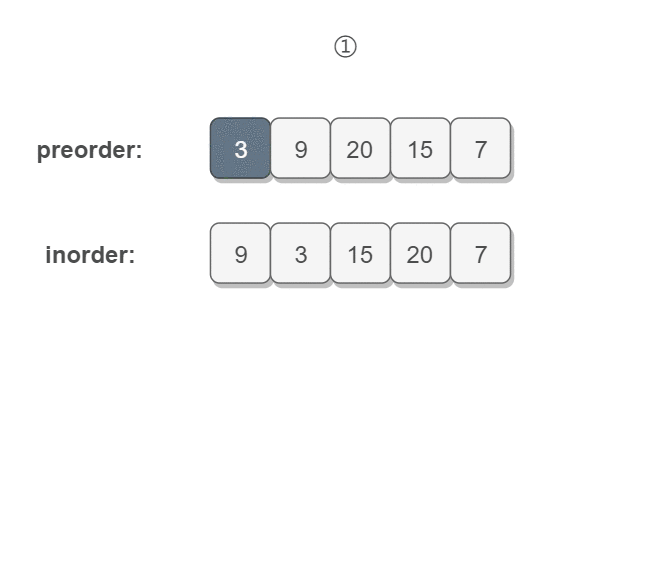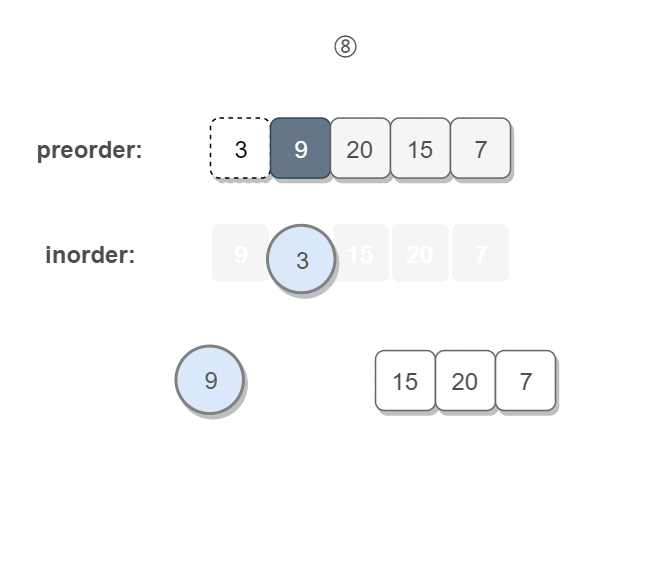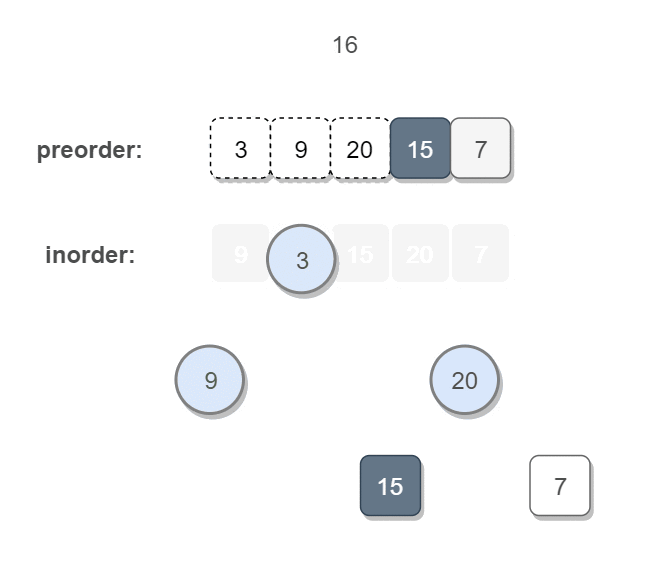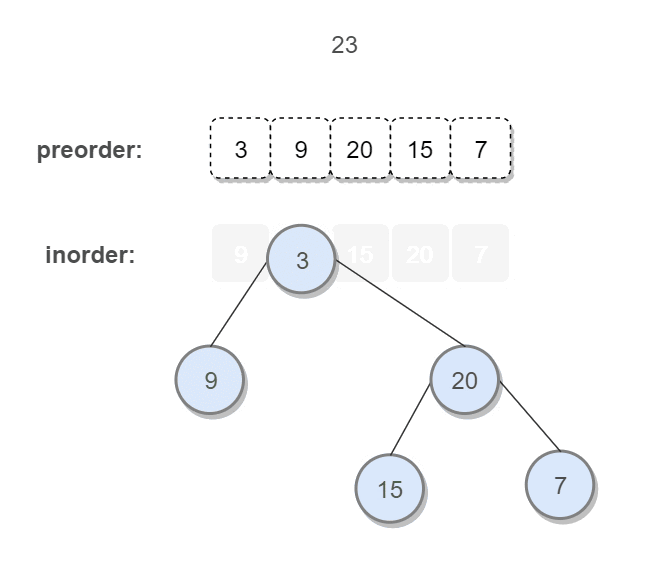
在这里插入图片描述
只要我们在中序遍历中定位到根节点，那么我们就可以分别知道左子树和右子树中的节点数目。

由于同一颗子树的 前序遍历 和 中序遍历 的 长度显然是相同 的，因此我们就可以对应到前序遍历的结果中，对上述形式中的所有左右括号进行定位。
这样以来，我们就知道了左子树的前序遍历和中序遍历结果，以及右子树的前序遍历和中序遍历结果，我们就可以递归地对构造出左子树和右子树，再将这两颗子树接到根节点的左右位置。

🍁代码：(C++、Java)

C++

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
private:unordered_map<int, int> index;//缓存中序遍历数组每个值对应的索引TreeNode* myBuildTree(const vector<int> preorder, int preL, int preR, int inL){if(preL > preR) return nullptr;// 前序遍历中的第一个节点就是根节点TreeNode* root = new TreeNode(preorder[preL]);// 在中序遍历中定位根节点int idx = index[root->val];// 得到左子树中的节点数目int len = idx - inL;root->left = myBuildTree(preorder, preL + 1, preL + len, inL);root->right = myBuildTree(preorder, preL + len + 1, preR, inL + len + 1);return root;}public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {for(int i = 0; i < preorder.size(); i++){index[inorder[i]] = i;}return myBuildTree(preorder, 0, preorder.size() - 1, 0);}
};

Java

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode(int x) { val = x; }* }*/
class Solution {private Map<Integer, Integer> index = new HashMap<>();//缓存中序遍历数组每个值对应的索引public TreeNode buildTree(int[] preorder, int[] inorder) {for (int i = 0; i < preorder.length; i++){index.put(inorder[i], i);}return myBuildTree(preorder, 0, preorder.length - 1, 0);}private TreeNode myBuildTree(int[] preorder, int preL, int preR, int inL){if(preL > preR) return null;// 前序遍历中的第一个节点就是根节点TreeNode root = new TreeNode(preorder[preL]);// 在中序遍历中定位根节点int idx = index.get(root.val);// 得到左子树中的节点数目int len = idx - inL;root.left = myBuildTree(preorder, preL + 1, preL + len, inL);root.right = myBuildTree(preorder, preL + len + 1, preR, inL + len + 1);return root;}
}

🚀 运行结果：

在这里插入图片描述

🕔 复杂度分析：

时间复杂度： $O (n)$ ，其中 n 是树中的节点个数。
空间复杂度： $O (n)$ ，除去返回的答案需要的 $O (n)$ 空间之外，我们还需要使用 $O (n)$ 的空间存储哈希映射，以及 $O (h)$ （其中 h 是树的高度）的空间表示递归时栈空间。这里 h < n，所以总空间复杂度为 $O (n)$ 。