数据结构【排序】
第七章 排序
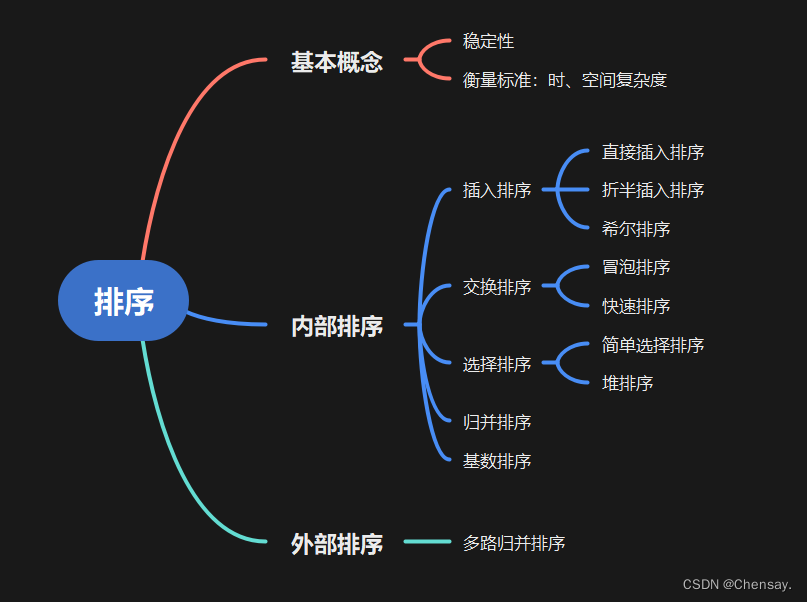
一、排序
1.定义:将无序的数排好序 ;
2.稳定性: Kᵢ和Kⱼ中,Kᵢ优先于Kⱼ那么在排序后的记录中仍然保持Kᵢ优先;
3.评价标准:执行时间和所需的辅助空间,其次是算法的稳定性;空间复杂度是O(1),代表其算法所需的辅助空间不依赖问题规模,则该排序方法为就地排序,否则就是非就地排序;
4.排序的分类:待排序的记录数不太多时为内部排序,反之为外部排序
二、插入排序
1.定义:按关键字大小插入到前面已经排好序的子序列中;
2.直接插入排序:稳定的排序;
- 性能分析:空间复杂度是O(1);最好的情况时间复杂度为O(n),最坏的时间复杂度为O(n²);
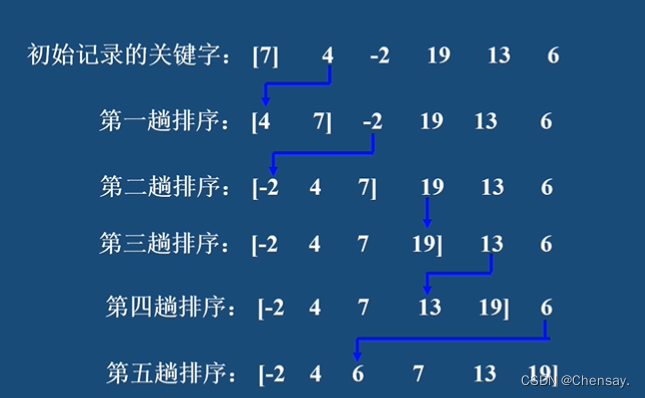
3.折半插入排序:是一种稳定的排序算法;有些类似折半查找;时间复杂度为O(n²);但对于数据量比较小排序表,折半插入排序往往能表现出较好的性能;

4.希尔排序
- 特点:分组后n值不断减小,关键字较小的记录跳跃式前移;
- 增量序列取法:无除1外的公因子;最后一个增量值必须为1;不稳定;
三、交换排序
1.定义:系统的交换反序的记录的偶对,直到不再有这样的偶对为止;
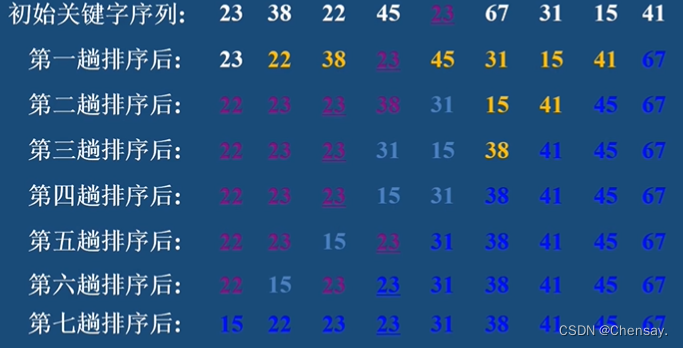
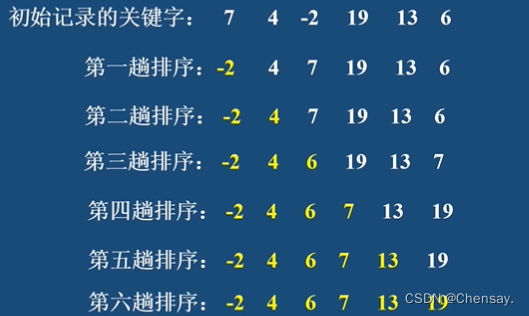
2.冒泡排序:时间复杂度T(n)=O(n²);空间复杂度S(n)=O(1);
3.快速排序 :两指针,选中的指针不动与另一个指针比较,若被比较的数小于选中的指针,就往选中指针的方向移动(也就是不做改变);否则就交换; 当两指针相遇时才完成第一次排序。
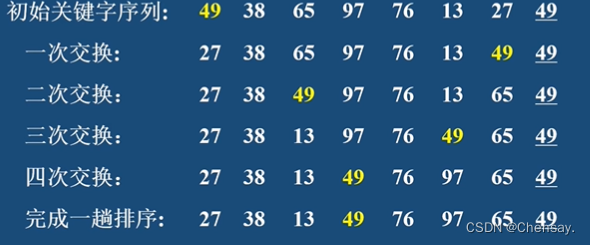
- 性能分析:时间复杂度是T(n)=O(nlog₂n),最坏情况是O(n²);栈最大深度为[log2n]+1;空间复杂度最坏是O(n);不稳定的算法;
四、选择排序
1.基本思想:每次从当前待排序的记录中选取关键字最小的记录表,然后与待排序的记录序列中的第一个记录进行交换,直到整个记录序列有序为止。
2.简单选择排序:时间复杂度是T(n)=O(n²),空间复杂度是S(n)=O(1);是不稳定的;
3.排序
- 定义:基于完全二叉树,分大根堆和小根堆;
- 结论:排序过程中,若采用的是小根堆,排序后得到的是非递减序列;若采用的是大根堆,则排序后得到的是非递增序列;
- 堆的调整和筛选:根结点必须小于左右子树,否则要交换;直到第一次全部交换完成输出对顶元素,也就是最小那个,然后将堆底元素送到堆顶,再进行排序交换;一直反复循环,直到堆只剩一个元素为止;
- 性能分析:时间复杂度是T(n)=O(nlog₂n),空间复杂度是S(n)=O(1);堆排序是不稳定的;
五、归并与基数排序
1.归并排序:时间复杂度为O(m+n);
- 排序思想:2-路归并排序,两两归并排序使其有序;
- 性能分析:时间复杂度无论最好还是最坏都是O(nlog₂n);空间复杂度是O(n);归并排序是稳定的;
2.基数排序(桶排序或数字排序):按待排序记录的关键字的组成成分(位)进行排序;
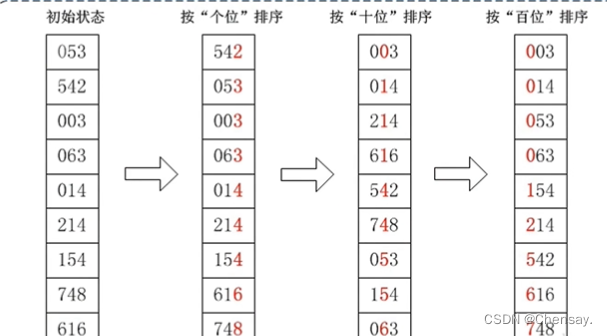
性能分析:时间复杂度O(d(n+r)),空间复杂度为O(n+r),其中d为关键字位数,每位有r种取值,排序的趟数是d;基数排序是稳定的;
六、各种排序的比较
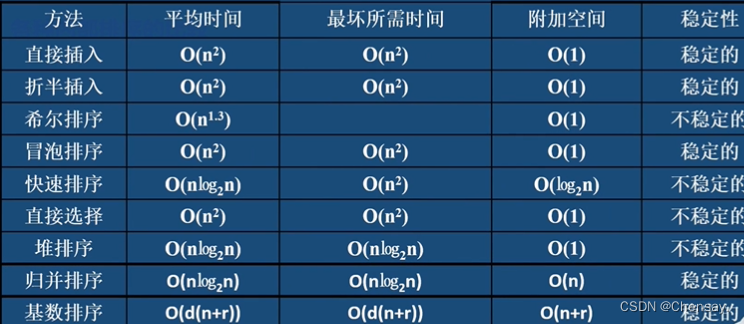
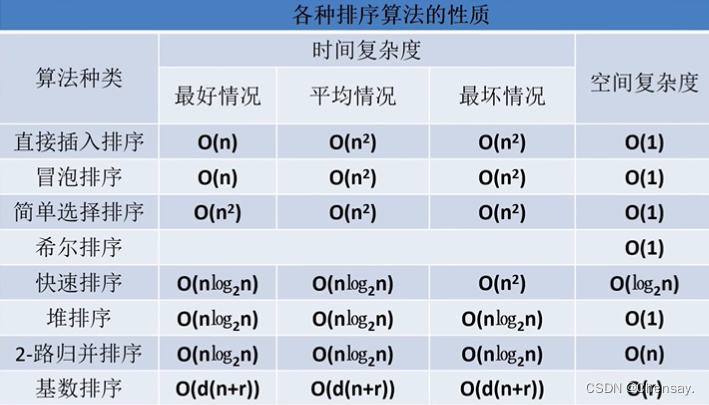
1.记忆方法:时间复杂度:快些归队(快速 归并堆排序)O(nlog₂n);
空间复杂度:快速O(log₂n)归并0(n)基数0(n+r) 其他都为0(1);
稳定性:快些选一堆(快速 希尔 选择 堆排序)是不稳定的;
2.其他细节:经过一次排序,能够保证一个关键字到达最终位置,这样的排序是交换的两类(冒泡、快速)和选择的两种(简单选择 堆);
- 排序算法的关键字比较次数和原始序列无关–简单选择和折半插入;
- 排序算法的排序趟数和原始序列有关–交换类的序。
