线性代数行列式的几何含义
行列式可以看做是一系列列向量的排列,并且每个列向量的分量可以理解为其对应标准正交基下的坐标。
行列式有非常直观的几何意义,例如:
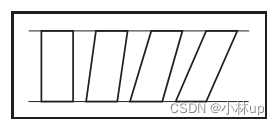
二维行列式按列向量排列依次是 a \mathbf{a} a和 b \mathbf{b} b,可以表示 a \mathbf{a} a和 b \mathbf{b} b构成的平行四边形的面积
∣ a b ∣ = ∣ ( x a x + y a y ) ( x b x + y b y ) ∣ = x a x b ∣ x x ∣ + x a y b ∣ x y ∣ + y a x b ∣ y x ∣ + y a y b ∣ y y ∣ = x a x b ( 0 ) + x a y b ( + 1 ) + y a x b ( − 1 ) + y a y b ( 0 ) = x a y b − y a x b . \begin{aligned} |\mathbf{a b}| & =\left|\left(x_{a} \mathbf{x}+y_{a} \mathbf{y}\right)\left(x_{b} \mathbf{x}+y_{b} \mathbf{y}\right)\right| \\ & =x_{a} x_{b}|\mathbf{x} \mathbf{x}|+x_{a} y_{b}|\mathbf{x y}|+y_{a} x_{b}|\mathbf{y} \mathbf{x}|+y_{a} y_{b}|\mathbf{y} \mathbf{y}| \\ & =x_{a} x_{b}(0)+x_{a} y_{b}(+1)+y_{a} x_{b}(-1)+y_{a} y_{b}(0) \\ & =x_{a} y_{b}-y_{a} x_{b} . \end{aligned} ∣ab∣=∣(xax+yay)(xbx+yby)∣=xaxb∣xx∣+xayb∣xy∣+yaxb∣yx∣+yayb∣yy∣=xaxb(0)+xayb(+1)+yaxb(−1)+yayb(0)=xayb−yaxb.
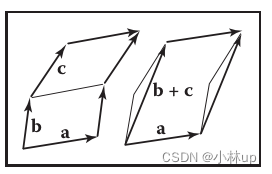
三维行列式按列向量排列依次是 a \mathbf{a} a, b \mathbf{b} b和 c \mathbf{c} c,可以表示 a \mathbf{a} a, b \mathbf{b} b和 b \mathbf{b} b构成的平行六面体的体积
∣ a b c ∣ = ∣ ( x a x + y a y + z a z ) ( x b x + y b y + z b z ) ( x c x + y c y + z c z ) ∣ = x a y b z c − x a z b y c − y a x b z c + y a z b x c + z a x b y c − z a y b x c . \begin{aligned} |\mathbf{a b c}| & =\left|\left(x_{a} \mathbf{x}+y_{a} \mathbf{y}+z_{a} \mathbf{z}\right)\left(x_{b} \mathbf{x}+y_{b} \mathbf{y}+z_{b} \mathbf{z}\right)\left(x_{c} \mathbf{x}+y_{c} \mathbf{y}+z_{c} \mathbf{z}\right)\right| \\ & =x_{a} y_{b} z_{c}-x_{a} z_{b} y_{c}-y_{a} x_{b} z_{c}+y_{a} z_{b} x_{c}+z_{a} x_{b} y_{c}-z_{a} y_{b} x_{c} . \end{aligned} ∣abc∣=∣(xax+yay+zaz)(xbx+yby+zbz)(xcx+ycy+zcz)∣=xaybzc−xazbyc−yaxbzc+yazbxc+zaxbyc−zaybxc.