平面坐标变换(单应性变换/Homography变换)
单应性(homography)变换用来描述物体在两个平面之间的转换关系,可以用于描述平移、翻转、缩放、旋转、仿射变换等。其是对应齐次坐标下的线性变换,可以通过矩阵表示:
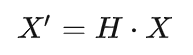
其中,H为单应性变换矩阵,假设变换前坐标为(x,y),变换后坐标为(x',y'),上式表达为:
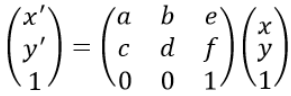
关于单应性变换的证明和实现可以参考:
(1条消息) 关于二维平面坐标变换矩阵的说明_二维坐标变换矩阵_JPy646的博客-CSDN博客
10、图像的几何变换——平移、镜像、缩放、旋转、仿射变换 - noticeable - 博客园 (cnblogs.com)
下面以翻转为例简单介绍其变换矩阵。假设图像的高和宽分别是h, w,那么:
水平翻转变换的单应性矩阵是:
[[-1, 0, w], [0, 1, 0], [0, 0, 1]]
将矩阵带入变换公式,可以得到实际的变换为:x' = w-x, y' = y。
垂直翻转变换的单应性矩阵是:
[[1, 0, 0], [0, -1, h], [0, 0, 1]]
对角线翻转变换的单应性矩阵是:
[[-1, 0, w], [0, -1, h], [0, 0, 1]]
先水平翻转再对角线翻转变换的单应性矩阵可以通过两个变换矩阵相乘(注意顺序是:对角线翻转矩阵*水平翻转矩阵)即可,也即是逆时针旋转90度,变换矩阵是:
[[1, 0, 0],
[0, -1, h],
[0, 0, 1]]
先垂直翻转再对角线翻转变换的单应性矩阵可以通过两个变换矩阵相乘(注意顺序是:对角线翻转矩阵*垂直翻转矩阵)即可,也即是顺时针旋转90度,变换矩阵是:
[[-1, 0, w],
[0, 1, 0],
[0, 0, 1]]
