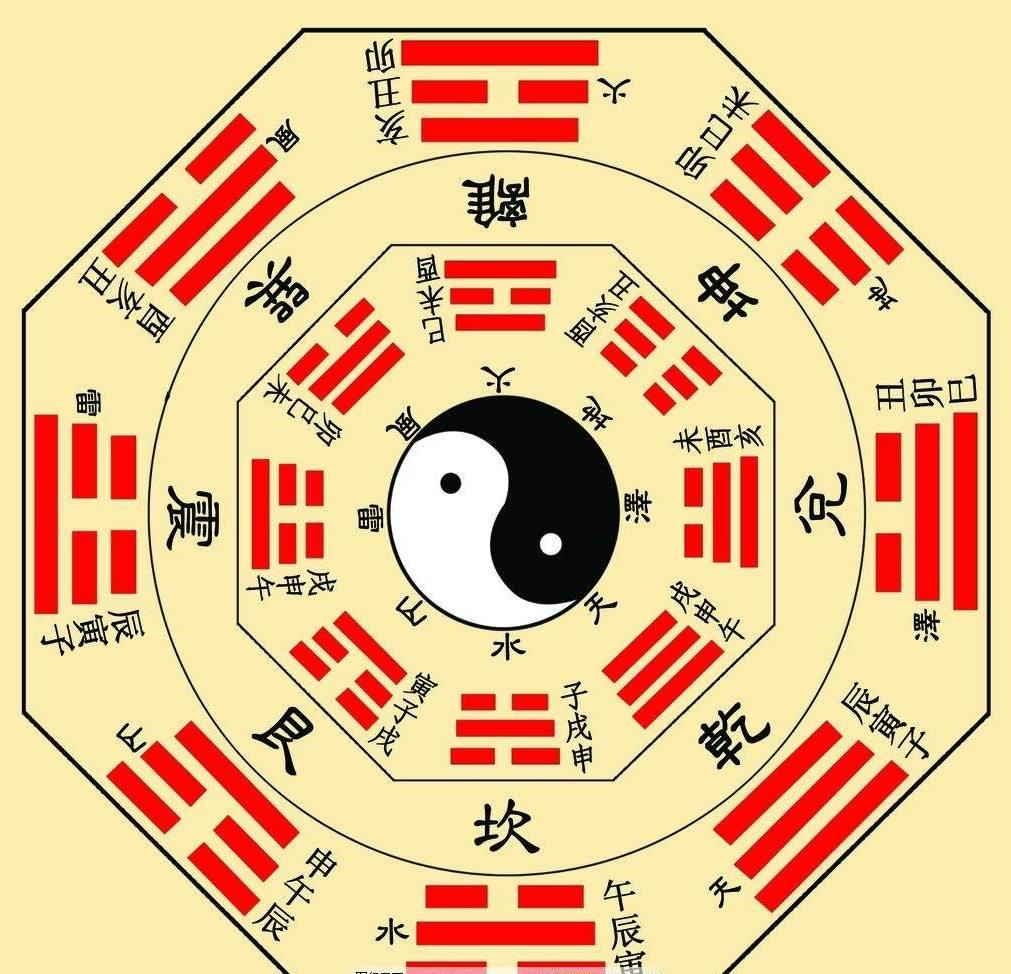
【伏羲八卦图】(PythonMatlab实现)
目录
1 与达尔文对话
2 与老子对话
2.1 Python实现
2.2 Matlab实现
1 与达尔文对话
140年前,1858年7月1日,达尔文在英伦岛发表了自己有关自然选择的杰出论文。他提出,生物的发展规律是物竞天择。经过物竞,自然界选择并存留最具生命优势的物种。这些物种愈竞愈强。直至人,已无所不能,成为统治世界的物种,这已是不争的事实。但在地球的漫长的演化史上,我们又看见,曾经统治地球的庞然大物恐龙消亡了。一-些科学家将其归之于小行星对地球的撞击。但就在我们这一代人眼前,兽中之王的老虎正在一天天消失。我们知道,在其消亡的时间轴上,小行星并未与地球碰撞。


循着达尔文的思索,我们得知:动物强于植物,老虎强于小鼠。愈是后续的物种愈强,因为它们是物竞天择的结果。强者存留,弱者淘汰。但环顾四野,植物茂盛,小鼠成群,而百兽之王的老虎却在一天天消亡。
进一步看,诞生于35亿年以前的最原始的物种单细胞生物,迄今仍然是地球上生存力度最强、生物质量最大、分布范围最广的生命形态,反而是那些在进化史上较晚近的高级物种如哺乳类动物正在以最快的速度灭绝。换一个眼光重新审视考古生物学,我们会发现,在亿万年来已遭灭绝的99%以上的生物品杀里,愈进化的物种淘汰几率愈高、绝种速度愈快,亦即生存力度愈低。
何以是“强”者消亡,“弱”者长存?即是说,在“物竞天择,适者生存”的表观现象后面,实际上暗藏着一个“自然选择偏偏要把最不适于生存的弱化产物层层推出”的单向度规定。印度诗圣泰戈尔说:“我们把世界看错了,反说世界欺骗了我们。”是伟大的达尔文错了,还是世界在我们有限的认知力之外,另有一番规律?
历代的哲人、物理学家、化学家、生物学家、社会学家,或思索过这一问题而不得其解,或已走到这一问题的门口,束手无策而返。其留下的大量艰涩难懂之文,多与此有关。


2 与老子对话
2.1 Python实现

#====导入相关库========
import turtle
import time#====欢迎关注公众号:电力系统与算法之美======
#====更多惊喜,更多浪漫,更多算法等你=====
angle = 270
turtle.title('我与老子对话')
#=====太极图=======
def tai():r = 200 # 设置半径turtle.penup() # 拿起画笔turtle.goto(0, 0) # 到画布中心turtle.setheading(angle) # 设置当前朝向为angle角度turtle.fd(r) # 前进r的距离turtle.pendown() # 放下画笔turtle.right(90) # 调整海龟角度#======画阳鱼======turtle.fillcolor("white") # 填充为白色turtle.begin_fill() # 开始填充turtle.circle(-r / 2, 180)turtle.circle(r / 2, 180)turtle.circle(r, 180)turtle.end_fill() # 填充结束#=====画阴鱼=========turtle.fillcolor("black") # 填充为黑色turtle.begin_fill()turtle.circle(r, 180)turtle.right(180)turtle.circle(-r / 2, 180)turtle.circle(r / 2, 180)turtle.end_fill()#=======画阴鱼眼==========turtle.penup()turtle.setheading(angle)turtle.fd(-r / 2)turtle.pendown()turtle.dot(r / 4, "white") # dot()绘制具有特定大小和颜色的圆点#=========画阳鱼眼=========turtle.penup()turtle.fd(-r)turtle.pendown()turtle.dot(r / 4, "black")turtle.penup()turtle.tracer(0) # 将刷新率置为0,即不刷新
for i in range(10000): # 这里设置了1w次,也可以是其他次数tai()turtle.update() # 更新绘图time.sleep(0.01) # 休眠时间,这一句可以没有,但是如果没有的话,太极转的会很快turtle.clear() # 清空画布angle += 1
2.2 Matlab实现


%% 太极八卦图%%~~~~~~~欢迎关注公众号:电力系统与算法之美~~~~%%clc;clear;close all;
t=0:.1:pi;
T=0:.1:2*pi;
c=@(t)cos(t);s=@(t)sin(t);
x=c(t);y=s(t);
X=c(t);Y=s(-t);
x1=.1*c(T)-.5;y1=.1*s(T);
x2=x1+1;%y2=y1;
x3=.5*c(t)-.5;y3=.5*s(t);
x4=x3+1;%y4=-y3;
hold on
f=@(x,y,c)fill([x,flip(x3,2),flip(x4,2)],...[y,flip(y3,2),flip(-y3,2)],c);
f(X,Y,'k');
f(x,y,'w');
fill(x2,y1,'k',x1,y1,'w')
axis square off
