当前位置：首页 > news >正文

字符串匹配算法--KMP算法--BM算法

news 2025/6/26 19:44:07

该算法解决的是字符串匹配问题，即查看字符串中是否含有完整的匹配字符串。如在java的string的contains方法

匹配问题最简单的就是暴力破解了。在java的contains也是这么实现的，效率是低一点的。如果想要更快的速度可以自己写KMP算法。

代码实现体验

Knuth-Morris-Pratt

KMP算法也不是特别高级的一种，只是对暴力法的一种优化，节省了很多不必要的匹配过程。
如

假定：
文本为A子串
匹配文本为B子串

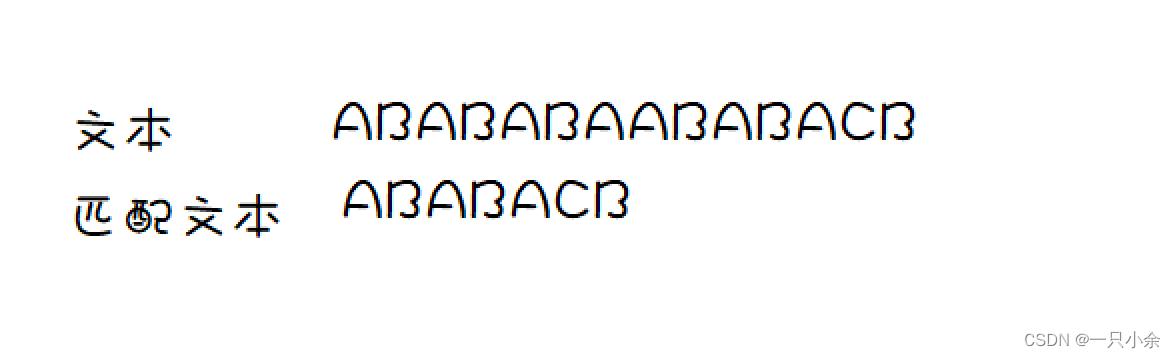
在这里插入图片描述
这里是相同的

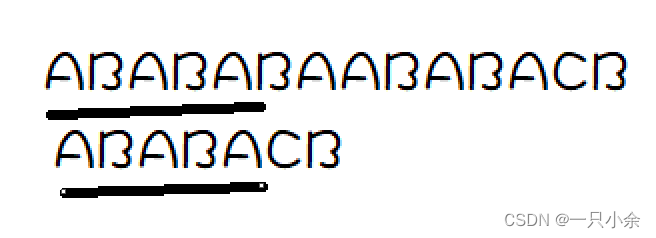
如果假定2号是匹配上的那么画线部分应该需要匹配上

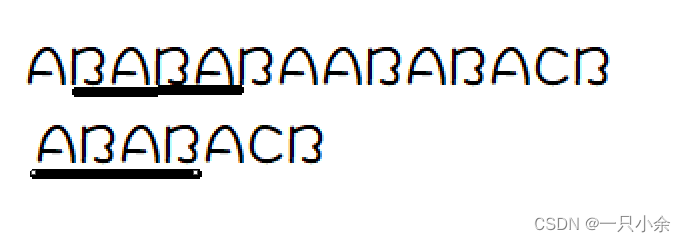
3号同理

这里可以看出来
如果匹配成功A后缀对应的会是匹配成功B前缀。
所以我们如果发现A后缀和B前缀相同就可以将B移动到那个位置。
我们会发现A后缀和B前缀都会是B的一部分(因为匹配成功了)
所以移动的位置只和B有关，我们就可以构建一个前缀表。如果匹配了 $i$ 个字符那么就移动 $n e x t [i]$ 位。

所以如何获取next表呢
用双指针
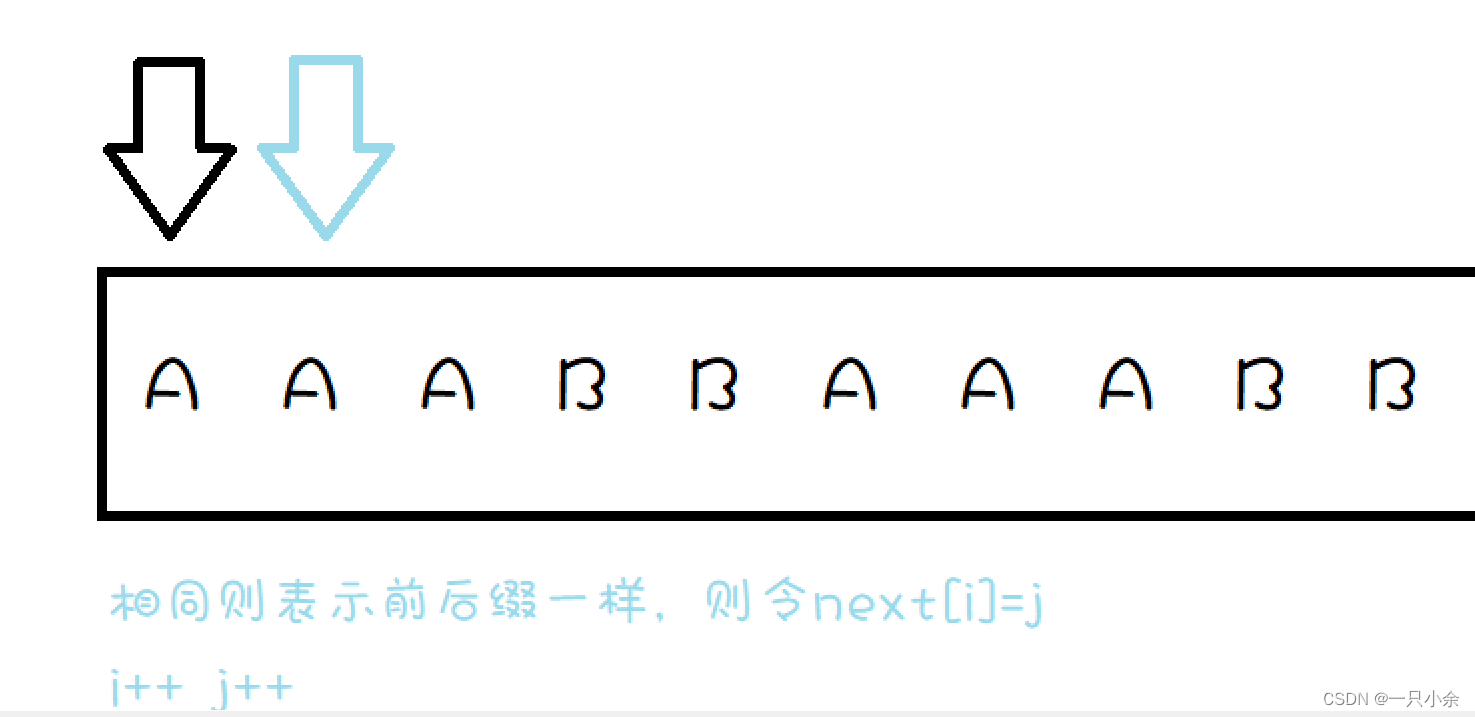
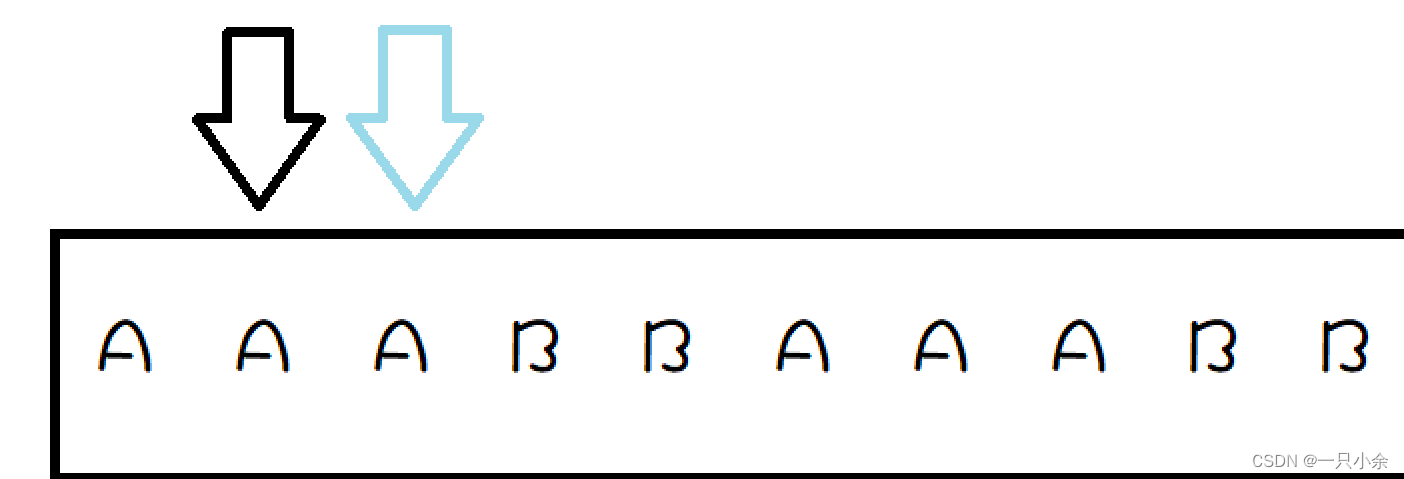
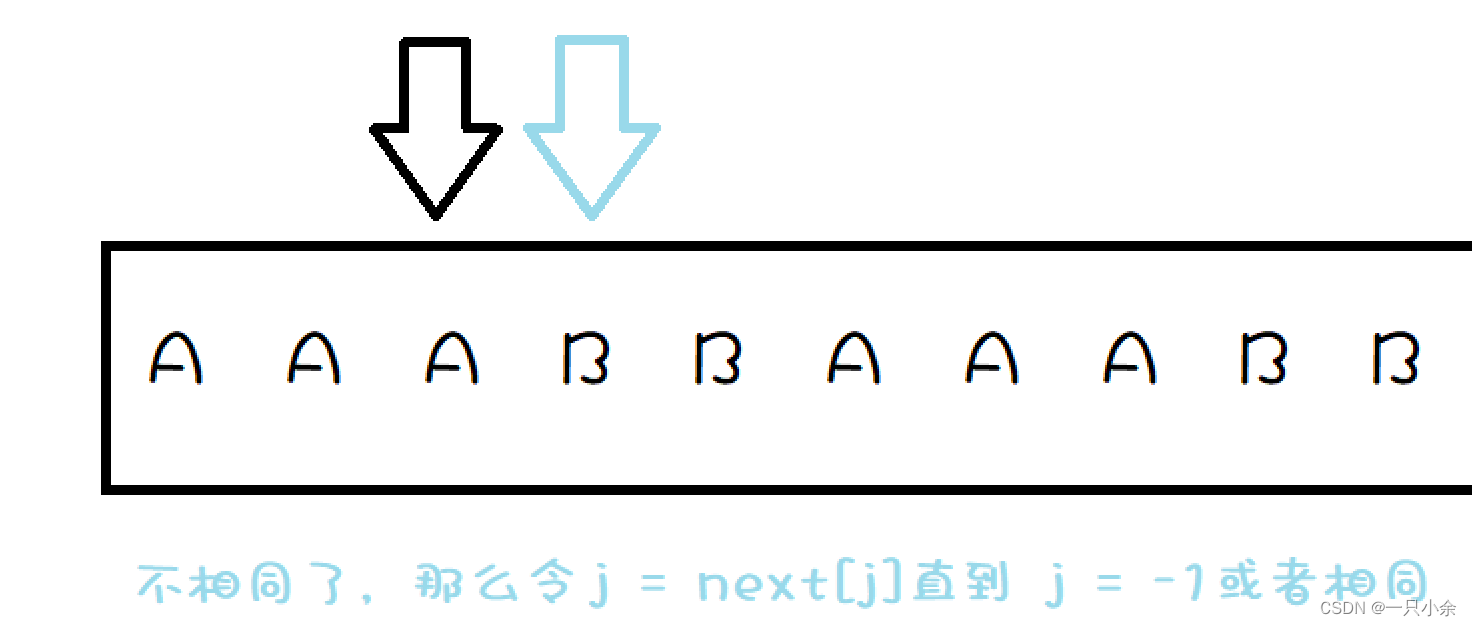
在这里插入图片描述

在这里插入图片描述

为什么呢：
这里利用的应该算动态规划的思想。
我们首先看next代表的是什么：

next代表对于前面部分匹配成功而最后一个匹配识别而指针指向的方向

那么我们可以知道上面的这个情况就等同于文本为AAAB匹配文为AAA的情况了。那么这个时候我们就需要将匹配文指针指向next[]

	protected static int[] getNext(String pattern) {// 初始化next数组和指针int[] next = new int[pattern.length()];next[0] = -1;// 后缀指针int i = 0;// 前缀指针int j = -1;// 生成next数组while (i < pattern.length() - 1) {// j == -1 代表j已经到了开头if (j == -1 || pattern.charAt(i) == pattern.charAt(j)) {i++;j++;next[i] = j;} else {j = next[j];}}return next;}

因为这个生成匹配next数组和这个的思想是一样的。这里直接给出代码了

  private static int KMPMatch(String text,String pattern,int[] next){int i = 0;int j = 0;while (i < text.length() && j < pattern.length()) {if (j == -1 || text.charAt(i) == pattern.charAt(j)) {i++;j++;} else {j = next[j];}}if (j == pattern.length())return i - j;elsereturn -1;}

在这里插入图片描述

Boyer-Moore

KMP算法是从左到右比较，而BM算法从右到左比较。而BM的这种做法也使得算法变得更简单了。

简化版本Horspool算法

就是从最后一个开始匹配如果没有匹配成功，则将离末尾最近的一个拿过来匹配。
如
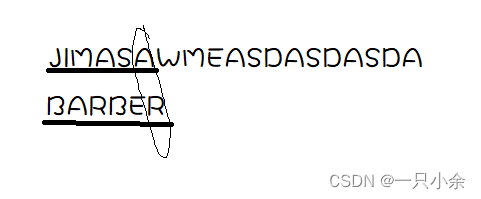
在这里插入图片描述
那么就将最近的A移动过来，然后继续从最后一位开始匹配

这样可以大大的减少匹配的次数。
为了加快移动的速度，我们可以用一个匹配表来加速。

如BARBER

A	B	E	R	其他
4	2	1	3	6

其代表的是
如果该字符串当前不匹配，那么字符串向右移动的距离。
代码
这里是用map实现的，也可以用数组实现。在最开始的运行代码里面有。

private static Map<Character, Integer> getTable(String pattern) {HashMap<Character, Integer> table = new HashMap<>();for (int i = 0; i < pattern.length() - 1; i++)table.put(pattern.charAt(i), pattern.length() - 1 - i);return table;}public static int horspool(String text, String pattern) {Map<Character, Integer> table = getTable(pattern);int offset = 0;while (offset <= text.length() - pattern.length()) {int i = pattern.length() - 1;while (i >= 0 && pattern.charAt(i) == text.charAt(offset + i)) i--;if (i < 0)return offset;else offset += table.getOrDefault(text.charAt(offset + pattern.length() - 1), pattern.length());}return -1;}

在这里插入图片描述

Boyer-Moore算法

BM算法是是在horspool算法的进一步优化。
然而在遇到第一个不匹配字符之前已经有k个字符匹配成功了，那么这2个算法的操作是不同的。

BM算法定义了两个规则：

坏字符规则：当文本串中的某个字符跟模式串的某个字符不匹配时，我们称文本串中的这个失配字符为坏字符，此时:
$移动位数d_1=max\{t_1(失配字符)-已经匹配字符数量,1\}$
$t_1的表和horspoll的是一样的$
好后缀规则：当字符失配时，已经匹配上的我们称为好后缀。
$移动位数d_2=后缀移动表t_2(匹配字符数量)$
总的移动 $max\{d_1,d_2\}$

坏字符我们已经学过了。
我们来看看好后缀是如何建表的。
好后缀就是相当于，在匹配文本中寻找本次已经匹配的后缀是否含有。
如下：
在这里插入图片描述

这个原理应该很好理解但是，代码怎么来实现呢。
getTable(pattern);就是上面的代码。

public static int match(String text, String pattern) {buildSuffixTable(pattern);getTable(pattern);int offset = 0;int l = pattern.length();while (offset <= text.length() - l) {int i = l - 1;while (i >= 0 && pattern.charAt(i) == text.charAt(offset + i)) {i--;}if (i < 0) {
//                System.out.println(offset + 1);
//                offset++;return offset;} else if (i == l - 1) {offset += table.getOrDefault(text.charAt(offset + i), l);} else {int d1 = Math.max(1, table.getOrDefault(text.charAt(offset + l - 1), l) - i);offset += Math.max(d1, gs[l - 1 - i]);}}return -1;}private static int[] gs;protected static void buildSuffixTable(String s) {char[] pattern = s.toCharArray();gs = new int[pattern.length]; // 模式串int[] suffix = new int[pattern.length];Arrays.fill(suffix, -1);for (int i = 1; i <= pattern.length - 1; i++) {int j = i - 1;int k = 0;while (j >= 0 && pattern[j] == pattern[pattern.length - 1 - k]) {j--;k++;suffix[k] = j + 1;}}
//        System.out.println(Arrays.toString(suffix));int i = 1;while (i < suffix.length && suffix[i] != -1) {gs[i] = pattern.length - i - suffix[i];i++;}int j = i - 1;while (j >= 0) {if (s.substring(s.length() - j).equals(s.substring(0, j))) {Arrays.fill(gs, i, gs.length, gs.length - j);break;}j--;}if (j == -1)Arrays.fill(gs, i, gs.length, gs.length);}